まずローレンツ力は要素内での電流密度と磁束密度より単位体積当たりの力として次の式で計算されます。
\begin{equation}
\boldsymbol{F}=[\boldsymbol{J}\times\boldsymbol{B}] \tag*{$(7.4-1)$}
\end{equation}
時間的に変化する動的な電磁解析や高周波解析では電磁力も時間的に変化します。過渡応答解析の場合は各時間ステップごとに（７．４－１）式を計算することによって電磁力が出力できます。
周波数応答解析の場合は単位時間当たりの平均値が出力されます。電流密度の実部虚部と磁束密度の実部虚部をつかうと、（７．１－３）式より次のようになります。
\begin{equation}
<\boldsymbol{F}>=\frac{1}{2}\bigl([\boldsymbol{J}_R\times\boldsymbol{B}_R]+[\boldsymbol{J}_I\times\boldsymbol{B}_I]\bigr) \tag*{$(7.4-2)$}
\end{equation}
ただし周波数をゼロに近づけていった極限では静解析と一致するはずですが、これで計算すると半分の値となります。
次にマックスウェルの応力による電磁力の計算ですが、これには二つの方法があります。物体全体に働く力としてそれを取り囲む面で（７．２－１１）式の表面積分をして求める方法と、この表面積分を体積積分で表した（７．２－１０）式を使って節点に働く力に変換する方法です。
まず、物体全体に働く力を求める場合は物体を取り囲む境界面における積分を行う必要があります。有限要素法では物体を取り囲む面は要素の面を使って表現します。
物体の周りの真空領域の要素で物体と接するものをすべて選び出し、これらの要素の物体と接する面についてマックスウェルの応力を計算し、この面の法線ベクトルとかけ合わせてこの面で積分します。これを選び出した要素すべてに対して足し合わせることによって物体に働く電磁力を求めます。
次の図では物体を網掛けの楕円で表しています。これに接する要素の一部を描いていますが、物体に接する面を選びます。この図では２次元的にかかれているので辺となっていますが３次元の場合は面となります。
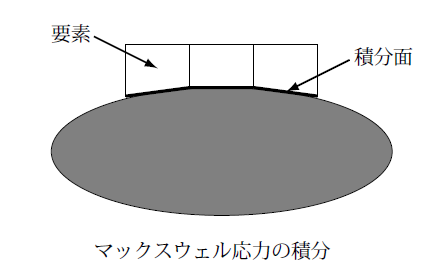
この場合はマックスウェルの応力テンソルとして、（７．２－８）式を使っても、（７．３－４）式や（７．３－８）式を使っても真空中の計算なので同じとなります。
次に電磁力を節点に割り振って節点ごとの力を求める節点力法とよばれる方法ですが、これは応力解析などで分布した力を節点ごとの力に変換して
荷重条件にする方法を電磁力に応用したものです。
応力解析では、応力テンソルを $\sigma_{ij}$ と表すとつり合い方程式は次のようになります。
\begin{equation}
\sum_j\frac{\partial\sigma_{ij}}{\partial x_j}+X_i=0 \notag
\end{equation}
ここに $\boldsymbol{X}$ は体積力です。この式と任意のベクトル関数 $\boldsymbol{w}$ との内積をとって解析領域 $V$ で積分すると、
\begin{equation}
\int_V\sum_iw_i\sum_j\frac{\partial\sigma_{ij}}{\partial x_j}dV+\int_V\sum_iw_iX_idV=0 \notag
\end{equation}
左辺第１項は部分積分とガウスの発散定理を使うと次のように変形できます。
\begin{equation}
\begin{split}
&\int_V\sum_{ij}\frac{\partial}{\partial x_j}(w_i\sigma_{ij})dV-\int_V\sum_{ij}\frac{\partial w_i}{\partial x_j}\sigma_{ij}dV \\
&=\int_S\sum_{ij}w_i\sigma_{ij}n_jdS-\int_V\sum_{ij}\frac{\partial w_i}{\partial x_j}\sigma_{ij}dV
\end{split} \notag
\end{equation}
ここに $S$ は領域 $V$ の境界面で $\boldsymbol{n}$ はその外向きにとった単位法線ベクトルです。この積分面が物体の外にあるのでこの積分はゼロとなります。
これより上の式は次のようにかけます。
\begin{equation}
-\int_V\sum_{ij}\frac{\partial w_i}{\partial x_j}\sigma_{ij}dV+\int_V\sum_iw_iX_idV=0 \notag
\end{equation}
有限要素法における応力解析ではこの方程式を解くのですが、節点要素が使われますのでこの $\boldsymbol{w}$ も節点ごとに離散化されます。
したがってこの方程式を離散化して連立方程式にすればこの式の左辺第２項は節点ごとのベクトルを並べたものになります。
これと左辺第１項が釣り合うのですから応力によって生ずる力は節点ごとに次のようになります。
\begin{equation}
f_i=-\sum_j\frac{\partial w_i}{\partial x_j}\sigma_{ij} \tag*{$(7.4-2)$}
\end{equation}
実際に節点力を求める場合は要素ごとの要素ベクトル、
\begin{equation}
F_{\alpha i}=\int_{V_n}\frac{\partial N_{\alpha i}}{\partial x_j}\sigma_{ij}dV \tag*{$(7.4-3)$}
\end{equation}
を作り、全ての要素について足し合わせて作った全体の列ベクトルの節点に対応する力のベクトルを求めることになります。
電磁力の場合マックスウェルの応力テンソルをこの応力テンソルとみなし同じように節点に働く力を求めようとするのです。
ここまでマックスウェルの応力テンソルとして(７．２－８)式の、
\begin{equation}
T_{ij}=\epsilon_0E_iE_j-\frac{\epsilon_0}{2}\boldsymbol{E}^2\delta_{ij}+\frac{1}{\mu_0}B_iB_j-\frac{1}{2\mu_0}\boldsymbol{B}^2\delta_{ij} \tag*{$(7.4-4)$}
\end{equation}
と、（７．３－４）式（７．３－８）式による、
\begin{equation}
T_{ij}=E_iD_j-\frac{\epsilon_0}{2}\boldsymbol{E}^2\delta_{ij}+H_iB_j-\frac{\mu_0}{2}(\boldsymbol{H}^2-\boldsymbol{M}^2)\delta_{ij} \tag*{$(7.4-5)$}
\end{equation}
を考えてきましたが同じ名前では混乱するので(７．４－４）式のテンソルをマックスウェルの応力テンソルとよび、(７．４－５）式のことを電磁応力テンソルとよぶことにします。
このように定義すると、もちろんここで使うテンソルは電磁応力テンソル(７．４－５）式を使うことになります。
ただし前にも言いましたようにこの電磁力はマクロな電磁場で表すことが出来るものであり、物質の密度変化に伴う誘電率や透磁率の変化、ピエゾや磁歪の効果は入っていないことに注意する必要があります。