まず電磁気学の基本的な法則であるクーロンの法則から始めます。この法則では電荷 $q$ が距離 $r$ 離れたところに作る電場 $E$ は次のようになります。
\begin{equation}
E=\frac{q}{4\pi\epsilon_0r^2} \tag*{$(3-1)$}
\end{equation}
ここに $\epsilon_0$ は真空中の誘電率です。この式は電場の大きさだけの関係を表していますが電場は方向を持ったベクトル量です。一つの電荷の作る電場の方向はこの電荷から放射状に広がる方向です。そこで電荷が原点にあるとして電場を測定する場所の位置ベクトルを太文字 $\boldsymbol{r}$ で表すと電場の方向はこの方向と一致するので電場ベクトルは次のようにかけます。
\begin{equation}
\boldsymbol{E}=\frac{q}{4\pi\epsilon_0r^2}\frac{\boldsymbol{r}}{r} \tag*{$(3-2)$}
\end{equation}
この電場は当然のことですが測定する位置によって変化しますので位置の関数と考えることができます。このようにベクトルが場所ごとに分布していることをベクトル場とよび、電場という言葉もこれによるものです。
私たちが日ごろ経験するベクトル場としては空気の流れである風や水の流れがあります。これらの速度も場所によってベクトルとして分布しているので速度場と考えることができます。ここで水の流れについて考えます。非常に大きな水槽の真ん中にあるホースの口から毎秒 $w$ リットルの水が流れ出しているとき、水はこの口から放射状に流れ出します。
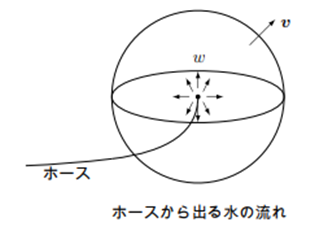
ここでは話をややこしくしないためにホースは非常に細く水の流れに影響しないものとします。水の流れはホースの口を中心とした球面から垂直に流れだすので、距離 $r$ 離れた場所では球面の面積と流速 $v$ の積がホースの口から流入する水の量と一致します。
\begin{equation}
4\pi r^2v=w \tag*{$(3-3)$}
\end{equation}
これよりホースの口から距離 $r$ 離れた場所の流速は次のようにかけます。
\begin{equation}
v=\frac{w}{4\pi r^2} \tag*{$(3-4)$}
\end{equation}
ベクトルでかくと、
\begin{equation}
\boldsymbol{v}=\frac{w}{4\pi r^2}\frac{\boldsymbol{r}}{r} \tag*{$(3-5)$}
\end{equation}
です。ここに $\boldsymbol{r}$ はホースの口を原点としたときの流速を測定する場所の位置ベクトルです。
この式を見ると電場に関するクーロンの法則(3-2)式と同じ形をしています。電場ベクトルに対応するのが流速ベクトル、電荷を真空中の誘電率で割ったものがホースの口から単位時間に流れ出す水の量に対応しています。
\begin{equation}
\begin{split}
&\boldsymbol{E} \hspace{10mm} \leftrightarrow \hspace{11mm} \boldsymbol{v} \\
&\frac{q}{\epsilon_0} \hspace{10mm} \leftrightarrow \hspace{10mm} w
\end{split} \notag
\end{equation}
この対応が成り立つのは水の密度が場所によって変化しないからで、そうでなければ半径 $r$ の球の領域に流入した水の量と球面から流出する水の量は等しくなりません。これより電場分布は密度が変化しない水の流速分布におきかえて考えることができます。このおきかえによってクーロンの法則の違った見方ができます。
原点から半径 $r$ の球とその中心に置かれたホースの口について考えてきたのですが、ここでホースの口を原点からずらしたときにどうなるかを考えます。この場合水の流れはもはや原点から放射状に広がる(3-5)式のような分布にはなりません。しかしこの場合も球の表面から流れ出る水量が $w$ であることは変わりません。
平面から単位面積当たり垂直に流れ出る単位時間の水の量は流速と一致しますが、流れがこの面と垂直でない場合はこの面の単位法線ベクトル $\boldsymbol{n}$ と流速ベクトルのなす角度 $\theta$ とすれば、
\begin{equation}
|\boldsymbol{v}||\boldsymbol{n}|\mathrm{cos}\theta\Delta S=\boldsymbol{v}\cdot\boldsymbol{n}\Delta S \notag
\end{equation}
の量の水が図のように面 $\Delta S$ から流出することになります。
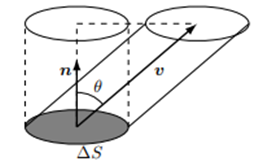
したがってこの球面から流出する水の量はこれを球面で面積分したものと一致します。
\begin{equation}
\int_S\boldsymbol{v}\cdot\boldsymbol{n}dS=w \tag*{$(3-6)$}
\end{equation}
これがホースの口が原点にあるときの(3-3)式に対応する式になりますが、ホースの口がこの球の内部であればどこでもよく一般的な式になっています。さらに考えている領域の形状は球に限らず閉じた面で囲まれていれば水の流入と流出の収支を表す式として常に成立します。領域の中にホースの口が一つではなく複数個あった場合も流入の収支を考えればホースの口から出る水の量を足し合わせたものが右辺の $w$ になることが分かります。電場について対応する式をかくと次のようになります。
\begin{equation}
\int_S\boldsymbol{E}\cdot\boldsymbol{n}dS=\frac{q}{\epsilon_0} \tag*{$(3-7)$}
\end{equation}
考えている積分面 $S$ に囲まれている体積領域 $V$ に複数の電荷がある場合はこの式の右辺の電荷 $q$ はそれらの和と考えることができます。さらに電荷が連続的に分布している場合は電荷の総量すなわち電荷密度 $\rho$ の体積積分として表わすことができます。
\begin{equation}
\int_S\boldsymbol{E}\cdot\boldsymbol{n}dS=\int_V\frac{\rho}{\epsilon_0}dV \tag*{$(3-8)$}
\end{equation}
この式は閉じた領域であればどのような形状についても成立し、クーロンの法則(3-2)式の異なった表現です。
もう少しこの式を調べるために体積領域 $V$ をこの内部の断面 $S_I$ で切り離して二つの領域に分割します。
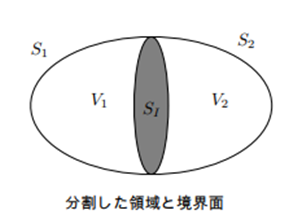
分割された領域を $V_1$ $V_2$ としそれを取り囲む面を $S_1$ $S_2$ とすればこれらの領域についても次の式が成り立ちます。
\begin{equation}
\begin{split}
&\int_{S_1}\boldsymbol{E}\cdot\boldsymbol{n}dS=\int_{V_1}\frac{\rho}{\epsilon_0}dV \\
&\int_{S_2}\boldsymbol{E}\cdot\boldsymbol{n}dS=\int_{V_2}\frac{\rho}{\epsilon_0}dV
\end{split} \tag*{$(3-9)$}
\end{equation}
これらの式の右辺は体積積分ですから、
\begin{equation}
\int_V\frac{\rho}{\epsilon_0}dV=\int_{V_1}\frac{\rho}{\epsilon_0}dV+\int_{V_2}\frac{\rho}{\epsilon_0}dV \tag*{$(3-10)$}
\end{equation}
が成立します。したがって左辺も次のような和の形でかける必要があります。
\begin{equation}
\int_S\boldsymbol{E}\cdot\boldsymbol{n}dS=\int_{S_1}\boldsymbol{E}\cdot\boldsymbol{n}dS+\int_{S_2}\boldsymbol{E}\cdot\boldsymbol{n}dS \tag*{$(3-11)$}
\end{equation}
この式が成立することは次のように考えれば理解できます。面積分の領域 $S$ は領域を分割することによって二つの面 $S_a$ $S_b$ に分割されます。(3-9)式の左辺にあらわれる面積分の領域はこれらの面と断面 $S_I$ により、
\begin{equation}
\begin{split}
&S_1=S_a+S_I \\
&S_2=S_b+S_I
\end{split} \tag*{$(3-12)$}
\end{equation}
です。ところでこれらの積分の断面 $S_I$ の寄与はその法線ベクトルが両者で逆を向いているのでキャンセルして面積分の和に寄与せずこのような分割が可能になります。さらに積分領域をもっと多くの小領域の和として表わすことができます。
\begin{equation}
\sum_n\int_{S_n}\boldsymbol{E}\cdot\boldsymbol{n}dS=\sum_n\int_{V_n}\frac{\rho}{\epsilon_0}dV \tag*{$(3-13)$}
\end{equation}
この式の右辺は(3-8)式の右辺を体積領域 $V_n$ に分割したもので、左辺の面積分 $S_n$ はこの体積領域を取り囲む境界面です。
少し式が複雑そうになってきましたが言っていることは簡単なことです。(3-8)式の領域をいくつかの領域に分割したときそれぞれの領域について、
\begin{equation}
\int_{S_n}\boldsymbol{E}\cdot\boldsymbol{n}dS=\int_{V_n}\frac{\rho}{\epsilon_0}dV \tag*{$(3-14)$}
\end{equation}
が成り立つのですが、単純に左辺と右辺を足し合わせた(3-13)式も成り立つということです。これが成立するのは最初の領域 $V$ の境界面以外の内部にできた面での積分がすべてキャンセルしてなくなってしまうからです。
さて、なぜこのような面倒くさいことをくどくどと言っているかというともう少しこの式を簡単に表現したいからです。小学生のころ図形の面積を求めるのに方眼紙の上に三角や、円を描きその図形に含まれるマス目を勘定したことがあるかと思いますがそれと同じことをしようとしているのです。このようにして求めた面積は図形の境界線が通るマス目をどう勘定するかによって異なりますので正しい面積からは少しずれますが大まかな面積は求まります。小学校のときには行いませんが方眼紙のマス目の大きさをどんどん小さくしていくと正しい面積に近づきます。
ここで考えている領域は3次元ですから $x$ 軸を幅 $\Delta x$ に分割し、同じように $y$ 軸と $z$ 軸をそれぞれ区間 $\Delta y$ $\Delta z$ で分割し領域に含まれる小さな直方体の和として領域を分割することを考えます。もちろんこのような分割では領域の境界面を含む直方体をどうするかという問題がありますが、面積を求めるときにマス目の大きさを小さくしていったようにこの直方体の大きさを小さくした極限を考えればよいと考えます。ここで、$x$ 方向の区間 $[a,a+\Delta x]$、$y$ 方向の区間 $[b,b+\Delta y]$、$z$ 方向の区間 $[c,c+\Delta z]$ で囲まれた直方体について考えます。この領域で(3-14)式の左辺を考えると面積分はこの直方体の六つの面に分割することができます。まず面 $x=a$ ではこの面の単位法線ベクトル $(-1,0,0)$ とこの面の中心における電場 $\boldsymbol{E}(a,b+\Delta y/2,c+\Delta z/2)$ から積分は次のようになります。
\begin{equation}
-E_x\bigl(a,b+\frac{\Delta y}{2},c+\frac{\Delta z}{2}\bigr)\Delta y\Delta z \notag
\end{equation}
ここでは非常に小さな領域を考えているので面の内部では電場の変化が一定であり、面積分を面の中心の値に面積をかけたものとしています。
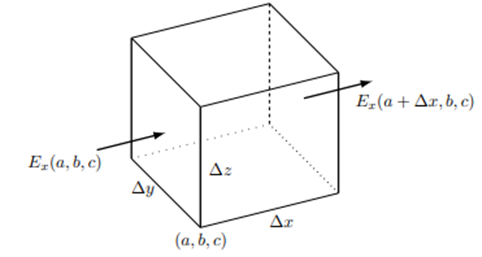
次に、面 $x=a+\Delta x$ ではこの面の単位法線ベクトル $(1,0,0)$ とこの面の中心における電場 $\boldsymbol{E}(a+\Delta x,b+\Delta y/2,c+\Delta z/2)$ から積分は次のようになります。
\begin{equation}
E_x\bigl(a+\Delta x,b+\frac{\Delta y}{2},c+\frac{\Delta z}{2}\bigr)\Delta y\Delta z \notag
\end{equation}
したがって両者の和は、
\begin{equation}
\begin{split}
&\bigl[E_x\bigl(a+\Delta x,b+\frac{\Delta y}{2},c+\frac{\Delta z}{2}\bigr)-E_x\bigl(a,b+\frac{\Delta y}{2},c+\frac{\Delta z}{2}\bigr)\bigr]\Delta y\Delta z \\
&=\frac{E_x\bigl(a+\Delta x,b+\frac{\Delta y}{2},c+\frac{\Delta z}{2}\bigr)-E_x\bigl(a,b+\frac{\Delta y}{2},c+\frac{\Delta z}{2}\bigr)}{\Delta x}
\Delta x\Delta y\Delta z
\end{split} \notag
\end{equation}
となります。この式の右辺は区間 $\Delta x$ をゼロに近づけた極限において変数 $x$ による偏微分となるので次のようにかくことができます。
\begin{equation}
\frac{\partial E_x}{\partial x}\Delta x\Delta y\Delta z \notag
\end{equation}
同様にして面 $y=b$ と面 $b+\Delta y$ についての積分は、
\begin{equation}
\frac{\partial E_y}{\partial y}\Delta x\Delta y\Delta z \notag
\end{equation}
面 $z=c$ と面 $c+\Delta z$ についての積分は、
\begin{equation}
\frac{\partial E_z}{\partial z}\Delta x\Delta y\Delta z \notag
\end{equation}
となるので、結局(3-14)式の左辺は次のようになります。
\begin{equation}
\int_{S_n}\boldsymbol{E}\cdot\boldsymbol{n}dS=\bigl(\frac{\partial E_x}{\partial x}+\frac{\partial E_y}{\partial y}+\frac{\partial E_z}{\partial z}\bigr)
\Delta x\Delta y\Delta z \tag*{$(3-15)$}
\end{equation}
これより(3-13)式の左辺はこの右辺の和として次のように表すことができます。
\begin{equation}
\sum_n\int_{S_n}\boldsymbol{E}\cdot\boldsymbol{n}dS
=\sum_n\bigl(\frac{\partial E_x}{\partial x}+\frac{\partial E_y}{\partial y}+\frac{\partial E_z}{\partial z}\bigr)\Delta x\Delta y\Delta z \tag*{$(3-16)$}
\end{equation}
ここで右辺の和は領域に含まれる微小な直方体すべてについてとり、微分はこれらの直方体の中心における値です。したがって、直方体の大きさをゼロに近づけた極限において体積積分となります。また(3-16)式の左辺は(3-8)式の左辺と等しいことから次の関係が成立します。
\begin{equation}
\int_S\boldsymbol{E}\cdot\boldsymbol{n}dS=\int_V\bigl(\frac{\partial E_x}{\partial x}+\frac{\partial E_y}{\partial y}+\frac{\partial E_z}{\partial z}\bigr)dV \tag*{$(3-17)$}
\end{equation}
この式の左辺は面積分であり、右辺は体積積分となっており一般のベクトル場について成り立つ関係です。この関係式をガウスの発散定理と呼んでいます。
水や空気の流速ベクトルの場合もこの関係は成り立ち、次のようにかけます。
\begin{equation}
\int_S\boldsymbol{v}\cdot\boldsymbol{n}dS=\int_V\bigl(\frac{\partial v_x}{\partial x}+\frac{\partial v_y}{\partial y}+\frac{\partial v_z}{\partial z}\bigr)dV \tag*{$(3-18)$}
\end{equation}
この式の左辺はこの領域から単位時間に流れ出る流量すなわち発散を表していることから定理の名前となっています。先ほどのホースの口から水が流れ込む例ではこの右辺の被積分関数は、単位体積中にホースから流れ込む水の量を表していることになります。したがって、これを
\begin{equation}
\mathrm{div}\boldsymbol{v}=\frac{\partial v_x}{\partial x}+\frac{\partial v_y}{\partial y}+\frac{\partial v_z}{\partial z} \tag*{$(3-19)$}
\end{equation}
とかき、ベクトルの発散とよんでいます。これを使うとガウスの発散定理は次のようにかけます。
\begin{equation}
\int_V\mathrm{div}\boldsymbol{v}dV=\int_S\boldsymbol{v}\cdot\boldsymbol{n}dS \tag*{$(3-20)$}
\end{equation}
クーロンの法則に戻って(3-8)式はこの定理を使って左辺をかきなおすと、
\begin{equation}
\int_V\mathrm{div}\boldsymbol{E}dV=\int_V\frac{\rho}{\epsilon_0}dV \tag*{$(3-21)$}
\end{equation}
となりますが、この積分領域はどのような領域をとっても構わないので次の式が得られます。
\begin{equation}
\mathrm{div}\boldsymbol{E}=\frac{\rho}{\epsilon_0} \tag*{$(3-22)$}
\end{equation}
左辺は(3-19)式のように表わされるのでこの式はクーロンの法則を微分の関係として表現したものとなります。静的な電場の場合この式から(3-2)式が導かれます。
