前節では誘電体の分極電荷や磁性体の磁化電流にもローレンツ力が働くとしてマックスウェルの応力テンソルから電磁力が計算できることを示しました。
ところがこれによって誘電体や磁性体に働く電磁力をそのまま求めることはできません。計算できるのは孤立した物体の場合です。
この場合はこの物体を取り囲む面について(7.2-11)式、
\begin{equation}
f_i=\int_S\sum_jT_{ij}n_jdS \notag
\end{equation}
を計算することによってこの孤立した物体に働く電磁力が求まります。ここにこの積分面 $S$ が真空領域にあることが重要で、誘電体や磁性体内部では正しく電磁力を評価することはできません。この節ではこれについて少し詳しく検討していきます。
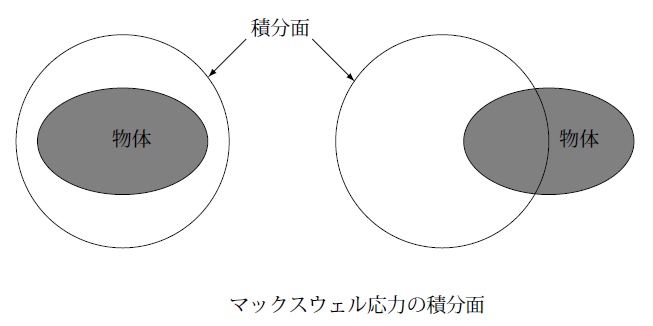
この図の左側は電磁力を求めようとしている物体を積分面が完全に取り囲んでいる場合です。このように積分面をとるとこの物体に働く力を正しく
計算することができます。
一方右側の図では積分面が物体の中を通っています。このとき積分面に囲まれた領域には物体の一部が入っていますのでこの物体の部分領域に働く力がこの積分で求めることができるでしょうか。残念ながらこの方法では正しい結果は得られません。
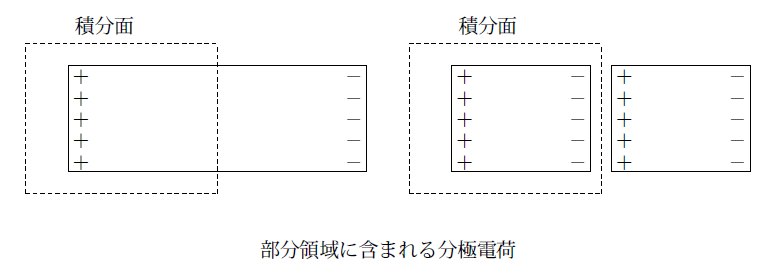
何故かを一様に分極した誘電体を例にとり説明します。下の図の左側はこの誘電体の部分領域をマックスウェル応力を計算する積分面で囲ったものです。
するとこの領域に含まれる分極電荷にローレンツ力が働きます。この場合誘電体が左方向に一様に分極していると考えていますので、分極電荷は左端にプラス、右端にマイナスの分極電荷が現れています。ですからこの積分面の内部にはプラスの分極電荷だけが存在していることになります。
(7.2-11)式による計算ではこの電荷で力を計算することになります。ところがこの積分面で囲まれる領域にある分極電荷はこれだけではありません。
右の図を見ていただければこの誘電体を真ん中で分割すれば、分割された断面に分極電荷が出てきます。
実は分割することによって現れたこの分極電荷は、分割しないときも存在します。ただこのような分極電荷は分割したときに現れるプラスとマイナスでキャンセルしているだけでつねに存在していると考える必要があります。
このように考えると左の図でも積分面で囲まれる領域にはこの左のプラス電荷だけでなく右側のキャンセルしているマイナスの分がこの領域に属していると考え、この電荷に働く力を加える必要があります。つまり右の図のように分割しない場合も積分面にあらわれる分極電荷を考える必要があります。
積分面にあらわれる分極電荷 $\sigma_p$ は分極ベクトルを $\boldsymbol{P}$、境界面の法線ベクトルを $\boldsymbol{n}$ とすれば次のようになります。
\begin{equation}
\sigma_p=(\boldsymbol{P}\cdot\boldsymbol{n}) \tag*{$(7.3-1)$}
\end{equation}
この電荷に働くローレンツ力の $i$ 成分は、境界面で積分して、
\begin{equation}
\int_S(\boldsymbol{P}\cdot\boldsymbol{n})E_idS=\int_SE_i\sum_jP_jn_jdS \tag*{$(7.3-2)$}
\end{equation}
となるのでこれを(7.2-11)式に加えると次のようになります。
\begin{equation}
\begin{split}
f_i&=\int_S\sum_jT_{ij}n_jdS+\int_SE_i\sum_jP_jn_jdS
=\int_S\sum_j\bigl(\epsilon_0E_iE_j-\frac{\epsilon_0}{2}\boldsymbol{E}^2\delta_{ij}\bigr)n_jdS+\int_SE_i\sum_jP_jn_jdS \\
&=\int_S\sum_j\bigl(E_i(\epsilon_0E_j+P_j)-\frac{\epsilon_0}{2}\boldsymbol{E}^2\delta_{ij}\bigr)n_jdS
\end{split} \notag
\end{equation}
ここで、
\begin{equation}
\epsilon_0E_j+P_j=D_j \notag
\end{equation}
なので次の式が得られます。
\begin{equation}
f_i=\int_S\sum_j\bigl(E_iD_j-\frac{\epsilon_0}{2}\boldsymbol{E}^2\delta_{ij}\bigr)n_jdS \tag*{$(7.3-3)$}
\end{equation}
ここでは磁場を考えていませんが、電場におけるマックスウェルの応力テンソルは次のようになります。
\begin{equation}
T_{ij}=E_iD_j-\frac{\epsilon_0}{2}\boldsymbol{E}^2\delta_{ij} \tag*{$(7.3-4)$}
\end{equation}
次に磁性体について考えます。磁性体の場合は磁化電流にローレンツ力が働きますが、この場合も誘電体と同じように部分領域を積分面で囲むとその表面にはキャンセルしていた磁化電流が現れます。
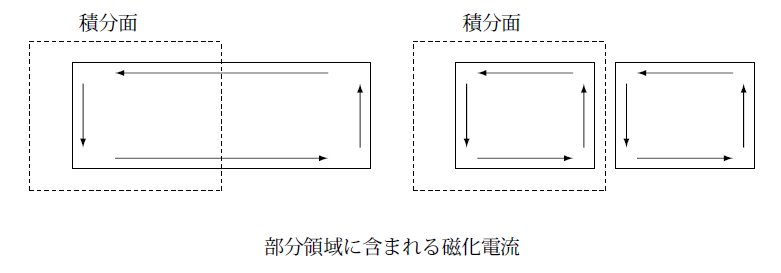
積分面にあらわれる表面磁化電流 $\boldsymbol{K}$ は磁化 $\boldsymbol{M}$ と境界面の法線ベクトル $\boldsymbol{n}$ によって、
\begin{equation}
\boldsymbol{K}=[\boldsymbol{M}\times\boldsymbol{n}] \tag*{$(7.3-5)$}
\end{equation}
と表されます。したがってこの磁化電流に働くローレンツ力は次のようになります。
\begin{equation}
\begin{split}
[\boldsymbol{K}\times\boldsymbol{B}]_i&=\sum_{jk}e_{ijk}K_jB_k=\sum_{jk}e_{ijk}\sum_{lm}e_{jlm}M_ln_mB_k \\
&=\sum_k\sum_{lm}(\delta_{kl}\delta_{im}-\delta_{km}\delta_{il})M_ln_mB_k \\
&=\sum_j(M_jn_i-M_in_j)B_j
\end{split} \tag*{$(7.3-6)$}
\end{equation}
これを積分面で積分し(7.2-11)式に加えると次のようになります。
\begin{equation}
\begin{split}
f_i&=\int_S\sum_jT_{ij}n_jdS+\int_S\sum_j(M_jn_i-M_in_j)B_jdS \\
&=\int_S\sum_j\bigl(\frac{1}{\mu_0}B_iB_j-\frac{1}{2\mu_0}\boldsymbol{B}^2\delta_{ij}\bigr)n_jdS+\int_S\sum_j(M_jn_i-M_in_j)B_jdS \\
&=\int_S\sum_j\bigl\{\bigl(\frac{1}{\mu_0}B_i-M_i\bigr)B_j-\bigl(\frac{1}{2\mu_0}\boldsymbol{B}^2-\boldsymbol{M}\cdot\boldsymbol{B}\bigr)\delta_{ij}\bigr\}n_jdS
\end{split} \notag
\end{equation}
ここで、
\begin{equation}
\frac{1}{\mu_0}B_i-M_i=H_i \notag
\end{equation}
であり、
\begin{equation}
\begin{split}
\frac{1}{2\mu_0}\boldsymbol{B}^2-\boldsymbol{M}\cdot\boldsymbol{B}&=\frac{1}{2}\bigl(\frac{1}{\mu_0}\boldsymbol{B}-2\boldsymbol{M}\bigr)\cdot\boldsymbol{B} \\
&=\frac{\mu_0}{2}(\boldsymbol{H}^2-\boldsymbol{M}^2)
\end{split} \notag
\end{equation}
なので電磁力は次のようになります。
\begin{equation}
f_i=\int_S\sum_j\bigl\{H_iB_j-\frac{\mu_0}{2}(\boldsymbol{H}^2-\boldsymbol{M}^2)\delta_{ij}\bigr\}n_jdS \tag*{$(7.3-7)$}
\end{equation}
これより磁場に関するマックスウェルの応力テンソルは次のようになります。
\begin{equation}
T_{ij}=H_iB_j-\frac{\mu_0}{2}(\boldsymbol{H}^2-\boldsymbol{M}^2)\delta_{ij} \tag*{$(7.3-8)$}
\end{equation}
これで誘電体と磁性体の部分領域に働く電磁力を求めることができました。ただし、実際の物体に対して電磁場の影響はこの電磁力だけではありません。
電磁場の影響はこの物質の自由エネルギーを変化させますのでそれに伴うマクロな電磁場で表現できない影響を考える必要があります。
例えば磁歪などです。
したがって、(7.3-4)式と(7.3-8)式から計算される電磁力はマクロな電磁場で表現できるもので実際の電磁力はこれ以外のものが含まれていることに注意する必要があります。これに対して物体全体に働く電磁力はマックスウェル応力から計算されるもので全て表現されています。
次に有限要素法による電磁場解析の結果として得られた電磁場から電磁力を求める方法について述べます。有限要素法の結果は、節点や辺における静電ポテンシャルやベクトルポテンシャルから求まります。これを使って要素内の電場や磁場が求まります。
技術情報 Techinicalinfo
- ホーム
- 技術情報
- 【技術情報】有限要素法入門
- 7.3 誘電体や磁性体に働く力
【技術情報】有限要素法入門
