ここまで電磁場解析に必要なベクトル解析について述べてきましたが、ここでまとめておきます。スカラー関数の勾配を求めるには、次のように行います。
\begin{equation}
\mathrm{grad}f(x,y,z)=\bigl(\frac{\partial f}{\partial x},\frac{\partial f}{\partial y},\frac{\partial f}{\partial z}\bigr) \tag*{$(5-1)$}
\end{equation}
これはベクトルであり方向はスカラー関数 $f$ の勾配方向で、大きさは勾配の大きさです。この右辺は次のようにかくことができます。
\begin{equation}
\bigl(\frac{\partial}{\partial x},\frac{\partial}{\partial y},\frac{\partial}{\partial z}\bigr)f(x,y,z) \notag
\end{equation}
このカッコで表した部分は偏微分の記号がベクトルの成分のように並んでいるのでつぎの記号を形式的なベクトルとして扱うことができます。
\begin{equation}
\boldsymbol{\nabla}\equiv\bigl(\frac{\partial}{\partial x},\frac{\partial}{\partial y},\frac{\partial}{\partial z}\bigr) \tag*{$(5-2)$}
\end{equation}
この $\boldsymbol\nabla$ という記号はナブラとよびベクトルであることを示すために太文字で表しています。
この $\boldsymbol{\nabla}$ や $\mathrm{grad}$ のような記号はスカラー関数から勾配ベクトルを作ります。このような作用を行うものを微分演算子とよんでいます。このように考えると、一変数関数の微分も、
\begin{equation}
\frac{df}{dx}=\frac{d}{dx}f(x) \notag
\end{equation}
とかき $d/dx$ を関数 $f(x)$ に作用する微分演算子とみることができます。
つぎにベクトルの発散は、
\begin{equation}
\mathrm{div}\boldsymbol{V}=\frac{\partial V_x}{\partial x}+\frac{\partial V_y}{\partial y}+\frac{\partial V_z}{\partial z} \tag*{$(5-3)$}
\end{equation}
です。ベクトルどうしの内積は、
\begin{equation}
\boldsymbol{A}\cdot\boldsymbol{B}=A_xB_x+A_yB_y+A_zB_z \notag
\end{equation}
ですが、(5-2)式をベクトルと考えると(5-3)式の右辺はベクトルである微分演算子 $\boldsymbol{\nabla}$ とベクトル $\boldsymbol{V}$ との内積の形をしています。
\begin{equation}
\boldsymbol{\nabla}\cdot\boldsymbol{V}=\bigl(\frac{\partial}{\partial x},\frac{\partial}{\partial y},\frac{\partial}{\partial z}\bigr)\cdot\boldsymbol{V}
=\frac{\partial}{\partial x}V_x+\frac{\partial}{\partial y}V_y+\frac{\partial}{\partial z}V_z \notag
\end{equation}
これよりベクトルの発散は、
\begin{equation}
\mathrm{div}\boldsymbol{V}=\boldsymbol{\nabla}\cdot\boldsymbol{V} \tag*{$(5-4)$}
\end{equation}
のようにかくことができます。
ベクトルの回転は、
\begin{equation}
\mathrm{rot}\boldsymbol{V}=\bigl(\frac{\partial V_z}{\partial y}-\frac{\partial V_y}{\partial z},
\frac{\partial V_x}{\partial z}-\frac{\partial V_z}{\partial x},\frac{\partial V_y}{\partial x}-\frac{\partial V_x}{\partial y}\bigr) \tag*{$(5-5)$}
\end{equation}
です。この式はベクトルの外積、
\begin{equation}
\boldsymbol{A}\times\boldsymbol{B}=(A_yB_z-A_zB_y,A_zB_x-A_xB_z,A_xB_y-A_yB_x) \notag
\end{equation}
であることを考えると、(5-5)式の右辺は次のようにかけます。
\begin{equation}
\bigl(\frac{\partial}{\partial x},\frac{\partial}{\partial y},\frac{\partial}{\partial z}\bigr)\times\boldsymbol{V}=\boldsymbol{\nabla}\times\boldsymbol{V} \notag
\end{equation}
これよりベクトルの回転は、
\begin{equation}
\mathrm{rot}\boldsymbol{V}=\boldsymbol{\nabla}\times\boldsymbol{V} \tag*{$(5-6)$}
\end{equation}
のようにかくことができます。
ここに出てきた微分演算子 $\mathrm{grad}$、$\mathrm{div}$、$\mathrm{rot}$ には次の性質があります。
\begin{equation}
\begin{split}
&\mathrm{grad}(f\pm g)=\mathrm{grad}f\pm\mathrm{grad}g \\
&\mathrm{div}(\boldsymbol{A}\pm\boldsymbol{B})=\mathrm{div}\boldsymbol{A}\pm\mathrm{div}\boldsymbol{B} \\
&\mathrm{rot}(\boldsymbol{A}\pm\boldsymbol{B})=\mathrm{rot}\boldsymbol{A}\pm\mathrm{rot}\boldsymbol{B}
\end{split} \tag*{$(5-7)$}
\end{equation}
演算子がこのような性質を持つ場合、線形演算子といいます。
これら微分演算子の関係のうち電磁気学によく出てくるものを次に示します。
\begin{equation}
\mathrm{rot}(\mathrm{grad}f)=0 \tag*{$(5-8)$}
\end{equation}
この関係は勾配ベクトルは回転をとればゼロになるということです。また回転の発散もゼロとなります。
\begin{equation}
\mathrm{div}(\mathrm{rot}\boldsymbol{V})=0 \tag*{$(5-9)$}
\end{equation}
これは次のようになるからです。
\begin{equation}
\mathrm{rot}(\mathrm{grad}f)=\bigl(\frac{\partial}{\partial y}\frac{\partial f}{\partial z}-\frac{\partial}{\partial z}\frac{\partial f}{\partial y},
\frac{\partial}{\partial z}\frac{\partial f}{\partial x}-\frac{\partial}{\partial x}\frac{\partial f}{\partial z},
\frac{\partial}{\partial x}\frac{\partial f}{\partial y}-\frac{\partial}{\partial y}\frac{\partial f}{\partial x}\bigr)
=(0,0,0) \notag
\end{equation}
\begin{equation}
\mathrm{div}(\mathrm{rot}\boldsymbol{V})=\frac{\partial}{\partial x}\bigl(\frac{\partial V_z}{\partial y}-\frac{\partial V_y}{\partial z}\bigr)
+\frac{\partial}{\partial y}\bigl(\frac{\partial V_x}{\partial z}-\frac{\partial V_z}{\partial x}\bigr)
+\frac{\partial}{\partial z}\bigl(\frac{\partial V_y}{\partial x}-\frac{\partial V_x}{\partial y}\bigr) = 0 \notag
\end{equation}
次に、
\begin{equation}
\Delta\equiv\mathrm{div}(\mathrm{grad})=\frac{\partial^2}{\partial x^2}+\frac{\partial^2}{\partial y^2}+\frac{\partial^2}{\partial z^2} \tag*{$(5-10)$}
\end{equation}
はラプラシアンという演算子でスカラー関数に作用させると次のようになります。
\begin{equation}
\Delta f=\boldsymbol{\nabla}\cdot\boldsymbol{\nabla}f=\frac{\partial^2f}{\partial x^2}+\frac{\partial^2f}{\partial y^2}+\frac{\partial^2f}{\partial z^2} \tag*{$(5-11)$}
\end{equation}
このラプラシアンに関しては次の関係もよく出てきます。
\begin{equation}
\mathrm{rot}(\mathrm{rot})=\mathrm{grad}(\mathrm{div})-\Delta \tag*{$(5-12)$}
\end{equation}
この関係も上でやったのと同じように成分ごとの比較を行って確認できますが少し面倒くさい式変形が必要です。このようなベクトルの成分についての計算は系統的な計算方法があり効率よく計算できますので付録で紹介しています。
ここからは電磁気で良く出てくる特別なベクトル場について考えていきます。例えば静電場の場合、電場 $\boldsymbol{E}$ に関して次の式が成り立ちます。
\begin{equation}
\mathrm{rot}\boldsymbol{E}=0 \tag*{$(5-13)$}
\end{equation}
つまり至る所で回転がゼロの渦無し場です。この場合ポテンシャル(電位)$\phi$ が定義でき、
\begin{equation}
\boldsymbol{E}=-\mathrm{grad}\phi \tag*{$(5-14)$}
\end{equation}
となることはよく知られています。このようなことがなぜ言えるのでしょうか。これは一般のベクトル場でも言えますのでこれ以降ベクトル場 $\boldsymbol{E}$ を電場に限らないものとします。まず、(5-13)式が成り立っていれば回転がゼロなので任意にとった閉曲線 $C$ について、
\begin{equation}
\oint_C\boldsymbol{E}\cdot\boldsymbol{t}dl=0 \tag*{$(5-15)$}
\end{equation}
となります。ここに $\boldsymbol{t}$ は閉曲線に沿った回転方向の単位ベクトルです。
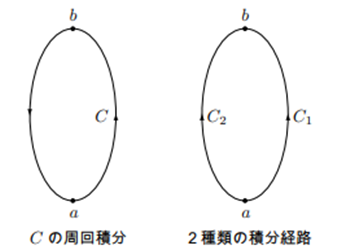
図の左側がこの積分を示していますが積分路に点 $a$ と点 $b$ があった場合次のようにかきかえることができます。
\begin{equation}
\oint_C\boldsymbol{E}\cdot\boldsymbol{t}dl=\int_{a右}^b\boldsymbol{E}\cdot\boldsymbol{t}dl+\int_{b左}^a\boldsymbol{E}\cdot\boldsymbol{t}dl \tag*{$(5-16)$}
\end{equation}
ただし右辺第1項の積分は右側の経路をとり、第2項の積分は左側の経路をとることを示すために積分記号の下に右と左の文字をかいています。したがって、
\begin{equation}
\int_{a右}^b\boldsymbol{E}\cdot\boldsymbol{t}dl+\int_{b左}^a\boldsymbol{E}\cdot\boldsymbol{t}dl=0 \notag
\end{equation}
です。ここで第2項の積分方向を逆にすれば積分の符号も逆になるので次のようになります。
\begin{equation}
\int_{a右}^b\boldsymbol{E}\cdot\boldsymbol{t}dl-\int_{a左}^b\boldsymbol{E}\cdot\boldsymbol{t}dl=0 \notag
\end{equation}
かきかえると、
\begin{equation}
\int_{a右}^b\boldsymbol{E}\cdot\boldsymbol{t}dl=\int_{a左}^b\boldsymbol{E}\cdot\boldsymbol{t}dl \tag*{$(5-17)$}
\end{equation}
です。右の図はこれを示したものです。このように点 $a$ から点 $b$ への線積分は二つの経路によらず同じであることが分かります。ここでの積分路は特別なものでなく、この二つの点を結ぶ経路であればどれをとっても積分値は同じになるということです。ここでベクトル $\boldsymbol{E}$ を電場とすればこの積分は点 $a$ と点 $b$ の間の電位差となります。これより例えば点 $a$ の電位を定義すれば点 $b$ の電位が一通りに決まります。静電場の場合電位という量が意味を持つのはこのような事情からです。実際(5-14)式より、
\begin{equation}
\int_a^b\boldsymbol{E}\cdot\boldsymbol{t}dl=-\int_a^b\mathrm{grad}\phi\cdot\boldsymbol{t}dl
=-\int_a^b\bigl(\frac{\partial\phi}{\partial x}t_xdl+\frac{\partial\phi}{\partial y}t_ydl
+\frac{\partial\phi}{\partial z}t_zdl\bigr) \notag
\end{equation}
ですが、
\begin{equation}
(t_xdl,t_ydl,tzdl)=(dx,dy,dz) \notag
\end{equation}
とかけるので上の式の右辺の積分は次のようになります。
\begin{equation}
\int_a^b\bigl(\frac{\partial\phi}{\partial x}dx+\frac{\partial\phi}{\partial x}dy+\frac{\partial\phi}{\partial x}dy\bigr)
=\int_a^bd\phi=\phi(b)-\phi(a) \notag
\end{equation}
したがってこの積分は積分路の両端での値だけで決まってしまい途中の積分路によらないことが分かります。逆に(5-13)式をみたさないベクトル場の場合、図の左のような積分路で周回積分を行ってもゼロとならず、右側の図のような積分が経路によって異なることになります。この場合は(5-14)式をみたすようなポテンシャルは存在しません。
次に発散がゼロとなるベクトル場を考えます。具体的には磁束密度 $\boldsymbol{B}$ がこのような場です。
\begin{equation}
\mathrm{div}\boldsymbol{B}=0 \tag*{$(5-18)$}
\end{equation}
このような場は次のように表すことができます。
\begin{equation}
\boldsymbol{B}=\mathrm{rot}\boldsymbol{A} \tag*{$(5-19)$}
\end{equation}
ここに $\boldsymbol{A}$ もベクトル場で、$\boldsymbol{B}$ が磁束密度の場合ベクトルポテンシャルとよばれています。まずベクトル $\boldsymbol{B}$ がこのようにベクトル場 $\boldsymbol{A}$ の回転で表されるとすれば、(5-9)式より回転の発散はゼロなので(5-18)式は自動的に成り立ちます。逆に(5-18)式をみたすベクトル場が必ず(5-19)式で表されるかということですが、これに関してはヘルムホルツの定理というのがあり、任意のベクトル場 $\boldsymbol{V}$ はスカラー場 $\phi$ の勾配とベクトル場 $\boldsymbol{A}$ の回転の和で表されます。
\begin{equation}
\boldsymbol{V}=\mathrm{grad}\phi+\mathrm{rot}\boldsymbol{A} \tag*{$(5-20)$}
\end{equation}
(5-18)式をみたすベクトル場 $\boldsymbol{B}$ にこの定理を適用すると次のようにかけます。
\begin{equation}
\boldsymbol{B}=\mathrm{grad}\phi+\mathrm{rot}\boldsymbol{A} \notag
\end{equation}
この式の両辺の発散をとると左辺は(5-18)式からゼロになり、右辺第2項も回転の発散なのでゼロになり、
\begin{equation}
\mathrm{div}\mathrm{grad}\phi=\Delta\phi=0 \notag
\end{equation}
となります。この式はラプラスの方程式ですが、無限遠点でスカラー場がゼロである場合は全空間で、
\begin{equation}
\phi=0 \notag
\end{equation}
となり、結局(5-19)式が成り立つということになります。
技術情報 Techinicalinfo
- ホーム
- 技術情報
- 【技術情報】ベクトル解析入門
- 5. 勾配、発散、回転の性質
【技術情報】ベクトル解析入門
