第6回 実行と結果
この段階まで来ますと後は計算を実行するのみとなります。
有限要素法では最終的に連立方程式に帰着され、その連立方程式を解くことにより、結果が得られます。
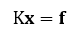
Kは係数マトリクス、xは解ベクトル、fは右辺ベクトルです。係数マトリクスKは、未知数の数をNとしますとN×Nの大規模な行列になります。
連立方程式を解く方法は大きく分けて、直接法と反復法があります。直接法は所定の回数で解くことができる方法です。
一方の反復法は言葉の通り反復計算により、近似解が得られる方法で、少ない反復回数で解が得られ、メモリも節約できます。
反復法で良く使われる手法として、ICCG法があります。
ICCG法はIncomplete Cholesky Conjugate Gradient methodの略です。
CG法(共役勾配法:Conjugate Gradient method)の前処理に不完全コレスキー分解(Incomplete Cholesky decomposition)を行う方法です。
前処理を施すことで、CG法の反復回数を減らして、早く解が得られます。
具体的なICCG法のアルゴリズムにご興味のある方は文献[1]などをご参照ください。
特に有限要素法の場合の係数マトリクスはゼロの要素が多くを占めています。このようなマトリクスを疎行列といいます。
実際に図6−1の有限要素法モデルで計算された係数マトリクスの非ゼロ要素分布を図6−2に示します。
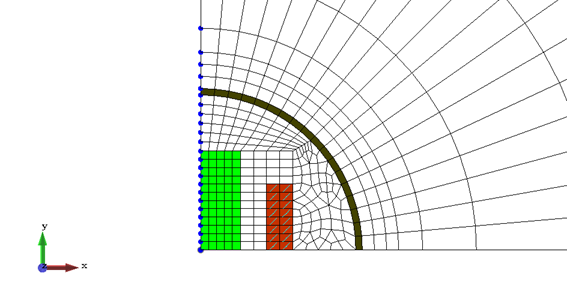
図6−1.有限要素法モデル(図4−9を再掲)
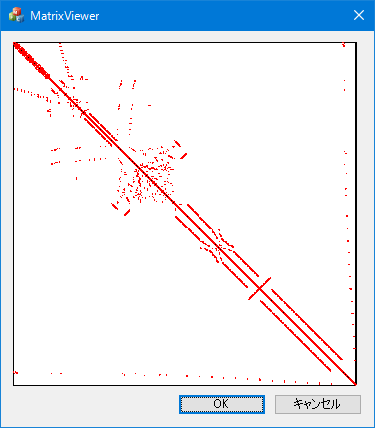
図6−2.非ゼロ要素分布
赤点が非ゼロ要素で、白い領域がゼロ要素を示しています。赤点が占める割合が小さく疎行列になっていることが確認できます。
このように疎行列であることから、行列全体に占める非ゼロ要素が少ないため、非ゼロ要素のみをメモリに保持することで、メモリが節約できます。
ある解析モデルを実行した際に表示される解析進行状況を図6−3に示します。
赤い線が横軸を横切ったとき、デフォルトのトレランスを満たし、収束したとします。場合によっては、厳しくすることもあります。
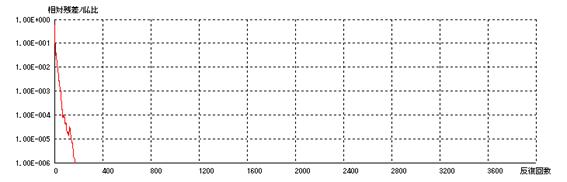
図6−3.解析進行状況
計算が途中で終了していないか、発散していないか解析進行状況で確認しておく必要があります。
収束していない場合などはベンダサポートや経験者に相談し、対処する必要があります。
非線形過渡解析の場合、実行を開始しますと、以下のような計算過程を進みます。
大雑把になりますが、計算過程を図6−4に示します。荷重条件や境界条件などは省略しています。
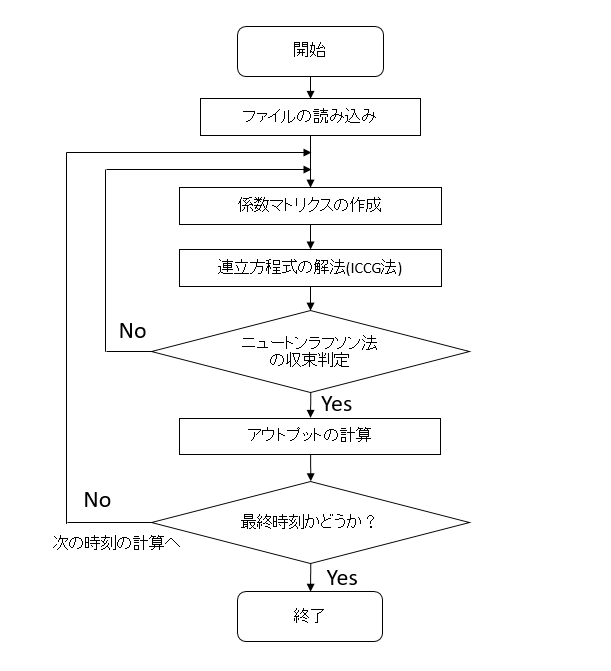
図6−4.計算過程
ある時刻の計算時のニュートンラフソン法(非線形計算の手法)のループごとにICCG法が動きますので、過渡解析、非線形解析では、解析のボリュームは大きくなります。
この計算過程を知っていますと、解析進行状況が把握しやすくなります。
これらの過程を経て、計算が収束すれば、解ベクトルxが計算されたことになります。
磁場解析の場合はこの解ベクトルは磁気ベクトルポテンシャル(A)です。磁束密度BとベクトルポテンシャルAは
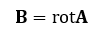
の関係があり、また、渦電流Jは電気伝導率をσとしますと、
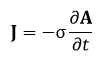
と表すことができますので、ベクトルポテンシャルがわかれば、磁束密度や渦電流が計算できます。
磁場解析で得られる結果としては、
磁束密度
磁場の強さ
磁化
渦電流密度
発熱密度
などがあり、これらはコンター図やベクトル図で分布を確認することができます。
また、
インダクタンス(磁気エネルギー)
電磁力
などは数値として出力されます。
磁束密度分布や渦電流密度分布についてはコンター図だけでなく、ベクトル図を表示させて、リーズナブルな結果になっているか確認が必要です。
磁束密度の流れを確認することで、メッシュや境界条件などの解析条件の不備を見つけることにつながります。
値の大きさも確認が必要です。磁束密度は常識的な大きさがありますので、あまりに大きい値の場合は条件やデータの見直しが必要になります。
●ポイント
解析進行状況から収束しているかどうか確認する。
ベクトル図で磁束密度や渦電流の流れを確認し、結果を吟味する。
●参考文献
[1] 朝倉現代物理学講座7 数値解析法 森 正武著 朝倉書店
これまで、6回に分けてご紹介致しました磁場解析入門講座は今回で終了致します。ここまでお読み頂きありがとうございました。
基本的な磁場解析のチュートリアルを実施される際に、
これらの知識がソフトウェアの操作と結びつき、理解が深まりますと大変ありがたいです。
また、実際にソフトウェアを操作して、磁場解析を体験して頂ける無料セミナーを開催しています。
セミナーのページ->
ご意見・ご感想は
こちらから->
