一般的な時間変化する場合(4.1-8)式、
\begin{equation}
\sigma\frac{\partial\boldsymbol{A}}{\partial t}+\mathrm{rot}\boldsymbol{H}=\boldsymbol{J} \notag
\end{equation}
を時間積分する必要があります。ここで左辺第2項は磁束密度を通してベクトルポテンシャルに依存しますのでこのまま直接積分することはできません。そこで数値積分を行うのですがそのためにここで少しだけ一般的な議論を行っておきます。
次のような時間微分を含む方程式を考えます。
\begin{equation}
\frac{d}{dt}x(t)=f(x) \tag*{$(4.3-1)$}
\end{equation}
この方程式は右辺が $x$ に依存しているため先ほどの電磁場の方程式同様このまま積分できません。
まず初期条件として時間 $t_a$ において、
\begin{equation}
x_a=x(t_a) \tag*{$(4.3-2)$}
\end{equation}
が分かっている場合、それよりのちの時刻 $t_b$ における $x_b$ は、
\begin{equation}
x_b=x_a+\int_{t_a}^{t_b}f(x)dt \tag*{$(4.3-3)$}
\end{equation}
により求まりますがこの積分が直接計算できません。そこで時間領域 $[t_a,t_b]$ を小さな区間に分割します。これはちょうど1次元の有限要素法で解析区間を有限要素に分割したのと同じことで、この領域内での変化が小さい場合は何らかの補間をして近似することができます。
ここで、
\begin{equation}
\begin{split}
&t_0=t_a \\
&t_N=t_b
\end{split} \notag
\end{equation}
として時間領域を、$[t_0,t_1],[t_1,t_2],\cdots,[t_{N-1},t_N]$ と $N$ 個の小領域に分割します。
すると、(4.3-3)式の右辺の積分は次のように表すことができます。
\begin{equation}
\int_{t_a}^{t_b}f(x)dt=\sum_{n=0}^{N-1}\int_{t_n}^{t_{n+1}}f(x)dt \tag*{$(4.3-4)$}
\end{equation}
このように時間領域を細かく分割すれば例えば時刻 $t_n$ までの $x$ が求まっておれば次の時刻 $t_{n+1}$ における値は、
\begin{equation}
x_{n+1}=x_n+\int_{t_n}^{t_{n+1}}f(x)dt \tag*{$(4.3-5)$}
\end{equation}
を計算することによって求まります。この式は(4.3-3)式と同じ形をしていますが積分する領域が小さいので、この区間における変化は単純な関数で近似してもそれほど精度の悪化を招かないことが期待できます。
一番簡単なのは一定の値をとる関数ですから、この区間で $x$ は一定となります。この一定値として分かっている時刻 $t_n$ における値 $x_n$ を使うと、
(4.3-5)式は、
\begin{equation}
x_{n+1}=x_n+\int_{t_n}^{t_{n+1}}f(x_n)dt=x_n+f(x_n)\Delta t \tag*{$(4.3-6)$}
\end{equation}
となります。ただし、
\begin{equation}
\Delta t=t_{n+1}-t_n \tag*{$(4.3-7)$}
\end{equation}
です。この右辺は既知の値なので計算することができます。このように既知の量だけを使って次の時刻 $t_{n+1}$ の値を求めることを陽解法といいます。
一定値として $t_{n+1}$ における値 $x_{n+1}$ を使うと次のようになります。
\begin{equation}
x_{n+1}=x_n+f(x_{n+1})\Delta t \notag
\end{equation}
この右辺第2項はまだ求まっていない $x_{n+1}$ を使っているのでこの項を左辺に移項すると次のようになります。
\begin{equation}
x_{n+1}-f(x_{n+1})\Delta t=x_n \tag*{$(4.3-8)$}
\end{equation}
この方程式を解いて $x_{n+1}$ を求める方法を陰解法といいます。陽解法が関数 $f$ に既知の値 $x_n$ を代入するのに比べてこの関数の中に未知である $x_n$ が入っているのでこの関数を解く必要があります。
陽解法にはこのように簡単に解けるという利点がありますが、数値的に安定な解が得られるかという保証がない場合があります。
数値的に安定性とは例えば下の図の左に示したように一定の振幅で振動している対象を解く場合、本来振幅が一定であるにもかかわらず右の図のように振幅がだんだん大きくなり最終的に非現実的な大きさとなるような場合は数値的に安定ではありません。
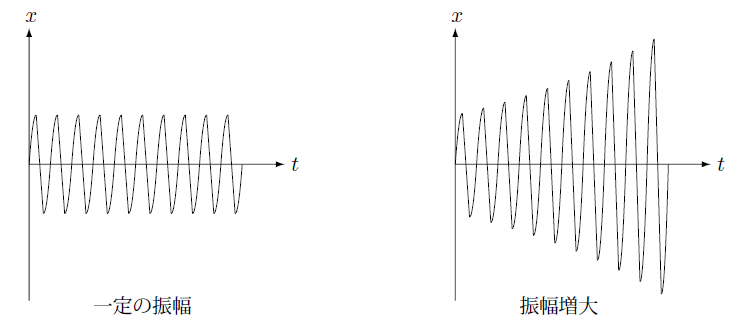
これに対して陰解法ではこのような問題を安定に解けることが分かっています。
積分する時間区間で関数を一定とするのは少し粗っぽい近似のようなので、次に関数が線形に変化する場合を考えます。
この場合時間区間 $[t_n,t_{n+1}]$ で関数は次のように近似できます。
\begin{equation}
f(t)=f_n+(f_{n+1}-f_n)\frac{t-t_n}{\Delta t} \tag*{$(4.3-9)$}
\end{equation}
ここで、
\begin{equation}
f_n=f(t_n) \notag
\end{equation}
としています。これを使うと(4.3-5)式は次のようになります。
\begin{equation}
\begin{split}
x_{n+1}&=x_n+\int_{t_n}^{t_{n+1}}\bigl\{f_n+(f_{n+1}-f_n)\frac{t-t_n}{\Delta t}\bigr\}dt \\
&=x_n+f_n\Delta t+\frac{f_{n+1}-f_n}{\Delta t}\bigl[\frac{t^2}{2}-tt_n\bigr]_{t_n}^{t_{n+1}} \\
&=x_n+\frac{1}{2}(f_n+f_{n+1})\Delta t
\end{split} \notag
\end{equation}
この場合も右辺にまだ求まっていない $f_{n+1}$ があるので次のように変形する必要があります。
\begin{equation}
x_{n+1}-\frac{1}{2}f(x_{n+1})\Delta t=x_n+\frac{1}{2}f(x_n)\Delta t \tag*{$(4.3-10)$}
\end{equation}
このようにして次の時刻の $x_{n+1}$ を求める方法はクランク・ニコルソン法とよばれています。この方法でも関数の内部に未知数を含むので陰解法とよばれます。これに対して先の陰解法を完全陰解法とよんでいます。
ここで、(4.3-6)(4.3-8)式とこの式を少し変形して比較すると次のようになります。
\begin{equation}
\begin{split}
&\frac{x_{n+1}-x_n}{\Delta t}=f(x_n) \\
&\frac{x_{n+1}-x_n}{\Delta t}=f(x_{n+1}) \\
&\frac{x_{n+1}-x_n}{\Delta t}=\frac{1}{2}\bigl\{f(x_n)+f(x_{n+1})\bigr\}
\end{split} \notag
\end{equation}
これらの式の左辺は(4.3-1)式の左辺の時間微分を数値的に離散化したものですから、最初の陽解法はこの微分をこの区間の最初の時刻 $t_n$ で決めており、完全陰解法では最後の時刻 $t_{n+1}$ で決めています。
また最後のクランク・ニコルソン法では最初の時刻に置ける関数の値と最後の時刻における関数の値の平均となっています。
ここで、$0$ から $1$ までの値をとるパラメータ $\theta$ を導入してこの関数値を次のように表してみます。
\begin{equation}
f_\theta=(1-\theta)f_n+\theta f_{n+1} \tag*{$(4.3-11)$}
\end{equation}
このパラメータを使うと上の式はまとめて次のようにかけます。
\begin{equation}
\frac{x_{n+1}-x_n}{\Delta t}=f_\theta=(1-\theta)f_n+\theta f_{n+1} \tag*{$(4.3-12)$}
\end{equation}
これより $\theta$ がゼロの場合が陽解法、$1$ のときが完全陰解法、$1/2$ のときがクランク・ニコルソン法となります。
このようにパラメータ $\theta$ を導入するとこれ以外の値を持つ場合についても考えることが出来ます。
この値をゼロから $1$ までいろいろと変えて数値的な安定性と、精度について調べると、$\theta$ がゼロに近い場合は不安定であり、$1$ に近づくほど数値的に安定となることが分かっています。また精度は逆にこのパラメータの値が小さいほど向上するといわれています。
したがって、数値解析の安定性と精度とはトレードオフの関係にあり磁場解析では $2/3$ がよく使われています。
もちろん厳密な積分と比較して、
\begin{equation}
\int_{t_n}^{t_{n+1}}f(x)dt=\bigl\{(1-\theta)f_n+\theta f_{n+1}\bigr\}\Delta t \notag
\end{equation}
となる $\theta$ は関数によって異なり次の図のようになります。
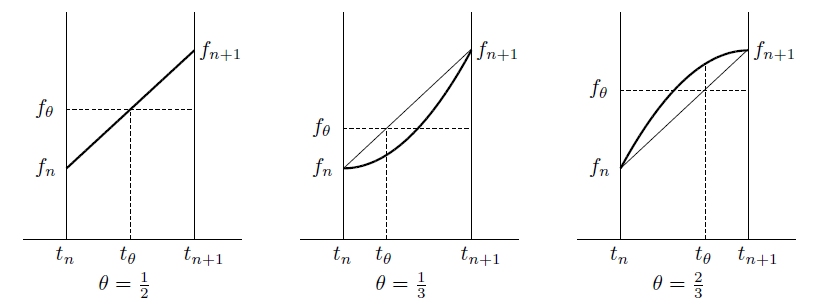
左は関数が直線的に変化する場合でこのときは $\theta$ が $1/2$ のとき厳密な積分と一致します。真ん中と右のグラフは関数が2次関数の場合で、中央のグラフでは $\theta$ が $1/3$、右のグラフでは $2/3$ のとき左辺の積分と一致します。
図から分かりますように $t_\theta$ での $f_\theta$ は関数値 $f(t_\theta)$ ではなく線形補関したときの値です。
準備が出来ましたのでここからは動的な磁場解析の話に戻します。この場合も今までやってきたことと同様に時間領域を短い時間区間に分割し、時刻 $t_n$ における電磁場が求まっており次の時刻 $t_{n+1}$ でどうなるかを調べることにします。
そこで基礎方程式である(4.1-8)式、
\begin{equation}
\sigma\frac{\partial\boldsymbol{A}}{\partial t}+\mathrm{rot}\boldsymbol{H}=\boldsymbol{J} \notag
\end{equation}
をこの時間区間 $[t_n,t_{n+1}]$ で解くことを考えます。そのために時刻 $t_\theta$ におけるベクトルポテンシャルや磁場、そして電流密度を次のように補間します。
\begin{equation}
\begin{split}
\boldsymbol{A}_\theta&=(1-\theta)\boldsymbol{A}_n+\theta\boldsymbol{A}_{n+1} \\
\boldsymbol{H}_\theta&=(1-\theta)\boldsymbol{H}_n+\theta\boldsymbol{H}_{n+1} \\
\boldsymbol{J}_\theta&=(1-\theta)\boldsymbol{J}_n+\theta\boldsymbol{J}_{n+1}
\end{split} \tag*{$(4.3-13)$}
\end{equation}
また時間を、
\begin{equation}
t=(1-\theta)t_n+\theta t_{n+1} \notag
\end{equation}
とすればベクトルポテンシャルの時間微分は次のようになります。
\begin{equation}
\frac{\partial\boldsymbol{A}}{\partial t}=\frac{\partial}{\partial\theta}\bigl\{(1-\theta)\boldsymbol{A}_n
+\theta\boldsymbol{A}_{n+1}\bigr\}\frac{\partial\theta}{\partial t}
=\frac{\boldsymbol{A}_{n+1}-\boldsymbol{A}_n}{\Delta t} \notag
\end{equation}
したがって基礎方程式はこの時間区間内で次のように表すことが出来ます。
\begin{equation}
\sigma\frac{\boldsymbol{A}_{n+1}-\boldsymbol{A}_n}{\Delta t}+\mathrm{rot}\bigl\{(1-\theta)\boldsymbol{H}_n+\theta\boldsymbol{H}_{n+1}\bigr\}
=(1-\theta)\boldsymbol{J}_n+\theta\boldsymbol{J}_{n+1} \notag
\end{equation}
ここで $\mathrm{rot}$ が線形演算子であることに注意して左辺に未知数が来るように変形すると、
\begin{equation}
\frac{\sigma}{\Delta t}\boldsymbol{A}_{n+1}+\theta\mathrm{rot}\boldsymbol{H}_{n+1}
=\boldsymbol{J}+\frac{\sigma}{\Delta t}\boldsymbol{A}_{n}-(1-\theta)\mathrm{rot}\boldsymbol{H}_{n} \tag*{$(4.3-14)$}
\end{equation}
となります。ただし電流密度は全て既知としていますのでまとめてかいています。
ちなみにこの方程式は導体の電気伝導率 $\sigma$ をゼロにすると、時間に依存しなくなり、
\begin{equation}
\boldsymbol{H}_{n+1}=\boldsymbol{H}_n \notag
\end{equation}
となるので静磁場の方程式
\begin{equation}
\mathrm{rot}\boldsymbol{H}_\theta=\boldsymbol{J}_\theta \notag
\end{equation}
となります。
次にこの方程式を空間を離散化して有限要素法を適用するのですが、異なっているのは導体の電気伝導率が入っている項です。
この項に関しては周波数応答解析の場合に定義した節点要素の要素行列、
\begin{equation}
C_{\alpha\beta}^{(n)}=\int_{V_n}N_\alpha\sigma N_\beta dV \notag
\end{equation}
または辺要素の要素行列、
\begin{equation}
C_{\alpha\beta}^{(n)}=\int_{V_n}\boldsymbol{N}_\alpha\cdot\sigma\boldsymbol{N}_\beta dV \notag
\end{equation}
を使うことが出来ます。
有限要素法では次に要素行列を解析領域の全ての要素に足し合わせた全体の行列方程式を作るのですが、まず線形磁性体から始めます。
線形磁性体では透磁率を $\mu$ とすれば、(4.3-14)式は次のようにかけます。
\begin{equation}
\frac{\sigma}{\Delta t}\boldsymbol{A}_{n+1}+\theta\mathrm{rot}\frac{1}{\mu}\mathrm{rot}\boldsymbol{A}_{n+1}
=\boldsymbol{J}_\theta+\frac{\sigma}{\Delta t}\boldsymbol{A}_{n}-(1-\theta)\mathrm{rot}\frac{1}{\mu}\mathrm{rot}\boldsymbol{A}_{n} \tag*{$(4.3-15)$}
\end{equation}
これより全体の行列方程式は次のようになります。
\begin{equation}
\bigl(\frac{1}{\Delta t}C+\theta K\bigr)A_{n+1}=F+\bigl\{\frac{1}{\Delta t}C-(1-\theta)K\bigr\}A_n \tag*{$(4.3-16)$}
\end{equation}
ここに $A_n$ と $A_{n+1}$ は時刻 $t_n$、$t_{n+1}$ におけるベクトルポテンシャルの列ベクトルです。
この方程式を解くと時刻 $t_{n+1}$ のベクトルポテンシャルが求まるので、これを繰り返すことによって離散化した時刻におけるベクトルポテンシャルを求めていくことが出来ます。
このように過渡応答解析では離散化された時刻、すなわち時間ステップにおいて電磁場を求めていくことが出来ます。
次に非線形磁性体の場合ですが等方性の場合について考えます。この場合、
\begin{equation}
\boldsymbol{H}=\frac{1}{\mu_0}\mathrm{rot}\boldsymbol{A}-\boldsymbol{M} \notag
\end{equation}
なので、(4.3-14)式は次のようにかけます。
\begin{equation}
\frac{\sigma}{\Delta t}\boldsymbol{A}_{n+1}+\theta\mathrm{rot}\bigl(\frac{1}{\mu_0}\mathrm{rot}\boldsymbol{A}_{n+1}-\boldsymbol{M}_{n+1}\bigr)
=\boldsymbol{J}_\theta+\frac{\sigma}{\Delta t}\boldsymbol{A}_{n}-(1-\theta)\mathrm{rot}\bigl(\frac{1}{\mu_0}\mathrm{rot}\boldsymbol{A}_n-\boldsymbol{M}_n\bigr) \notag
\end{equation}
非線形方程式を解くためにニュートン・ラプソン法を適用するためにベクトルポテンシャル $\boldsymbol{A}_{n+1}$ の修正分を $\Delta\boldsymbol{A}$ とおけば、上の式の $\boldsymbol{A}_{n+1}$ に $\boldsymbol{A}_{n+1}+\Delta\boldsymbol{A}$ を代入した式が成り立つことが要請されます。
\begin{equation}
\begin{split}
&\frac{\sigma}{\Delta t}(\boldsymbol{A}_{n+1}+\Delta\boldsymbol{A})
+\theta\mathrm{rot}\bigl\{\frac{1}{\mu_0}\mathrm{rot}(\boldsymbol{A}_{n+1}+\Delta\boldsymbol{A})-(\boldsymbol{M}_{n+1}+\Delta\boldsymbol{M})\bigr\} \\
&=\boldsymbol{J}_\theta+\frac{\sigma}{\Delta t}\boldsymbol{A}_{n}-(1-\theta)\mathrm{rot}\bigl(\frac{1}{\mu_0}\mathrm{rot}\boldsymbol{A}_n-\boldsymbol{M}_n\bigr)
\end{split} \notag
\end{equation}
ここに、
\begin{equation}
\Delta\boldsymbol{M}=\frac{\partial\boldsymbol{M}}{\partial\boldsymbol{B}}\mathrm{rot}\Delta\boldsymbol{A} \notag
\end{equation}
です。これを上の式に代入して左辺に $\Delta\boldsymbol{A}$ が来るように変形すると次のようになります。
\begin{equation}
\begin{split}
&\frac{\sigma}{\Delta t}\Delta\boldsymbol{A}
+\theta\mathrm{rot}\bigl(\frac{1}{\mu_0}-\frac{\partial\boldsymbol{M}}{\partial\boldsymbol{B}}\bigr)\mathrm{rot}\Delta\boldsymbol{A} \\
&=\boldsymbol{J}_\theta+\frac{\sigma}{\Delta t}\boldsymbol{A}_{n}-(1-\theta)\mathrm{rot}\bigl(\frac{1}{\mu_0}\mathrm{rot}\boldsymbol{A}_n-\boldsymbol{M}_n\bigr) \\
&-\frac{\sigma}{\Delta t}\boldsymbol{A}_{n+1}-\theta\mathrm{rot}\bigl(\frac{1}{\mu_0}\mathrm{rot}\boldsymbol{A}_{n+1}-\boldsymbol{M}_{n+1}\bigr)
\end{split} \notag
\end{equation}
これより全体の行列方程式は次のようになります。
\begin{equation}
\bigl(\frac{1}{\Delta t}C+\theta K^\ast\bigr)\Delta A=F+M+\bigl\{\frac{1}{\Delta t}C-(1-\theta)K\bigr\}A_n
-\bigl(\frac{1}{\Delta t}C+\theta K\bigr)A_{n+1} \tag*{$(4.3-17)$}
\end{equation}
ここに、
\begin{equation}
M=(1-\theta)M_n+\theta M_{n+1} \notag
\end{equation}
です。
過渡応答解析の場合時間ステップごとに次々と電磁場を求めていくのですが、各時間ステップでニュートン・ラプソン法による繰り返し計算が必要になります。
時刻 $t_n$ ステップに入るとまずベクトルポテンシャルの初期値を設定します。この初期値としてはゼロや前の時間ステップの結果が使われています。
非線形磁性体を含む過渡応答解析では、このように時間ステップごとにニュートン・ラプソン法の繰り返しが必要なので時間ステップの数が多いと多くの計算時間が必要になります。そこで精度を保ちつつできるだけ時間ステップの幅を大きくとることが必要になります。
ここまで述べてきたことから過渡応答解析の時間の離散化の近似では時間ステップ間でベクトルポテンシャルが線形変化をしているとしていましたので、この時間間隔の間に電磁場が直線的に変化しているとみなせる程度の大きさが望ましいと思われます。
例えば周期的な変化の場合1周期を何分割すればよいかですが、角周波数 $\omega$ として、
\begin{equation}
f(t)=\mathrm{sin}\omega t \notag
\end{equation}
で表される関数の1周期を8分割したのが下の図です。
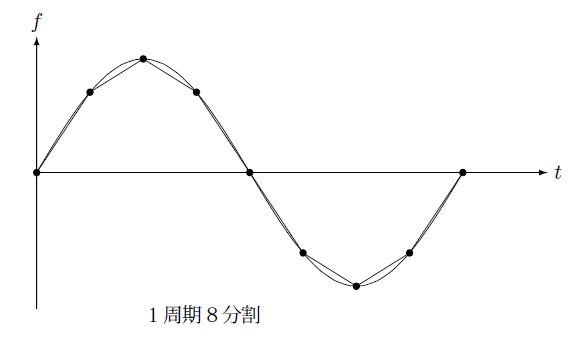
この図を見ると一周期 $[0,2\pi]$ として最初区間の $[0,\pi/4]$ は比較的直線的に変化していますが、次の区間 $[\pi/4,\pi/2]$ では関数の形は直線的な変化から少しずれています。もちろん何を問題とするかで必要とされる精度は異なりますので問題によって時間ステップの幅を決める必要があります。
技術情報 Techinicalinfo
- ホーム
- 技術情報
- 【技術情報】有限要素法入門
- 4.3 過渡応答解析
【技術情報】有限要素法入門
