2次元の場合(1.1-6)式は次のようになります。
\begin{equation}
\frac{\partial}{\partial x}\bigl(\epsilon\frac{\partial\phi}{\partial x}\bigr)
+\frac{\partial}{\partial y}\bigl(\epsilon\frac{\partial\phi}{\partial y}\bigr)=-\rho \tag*{$(1.3-1)$}
\end{equation}
1次元の場合は解析領域は数直線上の区間でしたが、2次元の場合は平面上の閉じた領域となります。
1次元のときと同様にこの方程式に任意関数 $w(x,y)$ を両辺にかけて解析領域 $S$ で積分します。
\begin{equation}
\int_Sw(x,y)\bigl[\frac{\partial}{\partial x}\bigl(\epsilon\frac{\partial\phi}{\partial x}\bigr)
+\frac{\partial}{\partial y}\bigl(\epsilon\frac{\partial\phi}{\partial y}\bigr)\bigr]dS=-\int_Sw(x,y)\rho dS \tag*{$(1.3-2)$}
\end{equation}
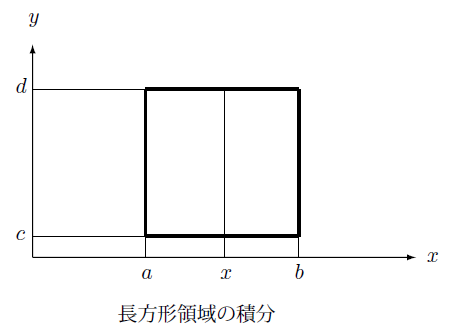
ここで2次元の解析領域 $S$ での積分について説明します。下の図のようにこの領域 $S$ が長方形の場合は、被積分関数を $f(x,y)$ としたとき次のように積分できます。
\begin{equation}
\int_Sf(x,y)dS=\int_c^d\int_a^bf(x,y)dxdy \notag
\end{equation}
ところが一般の2次元の解析領域は長方形と限らず下の図のように曲線で囲まれている場合があります。
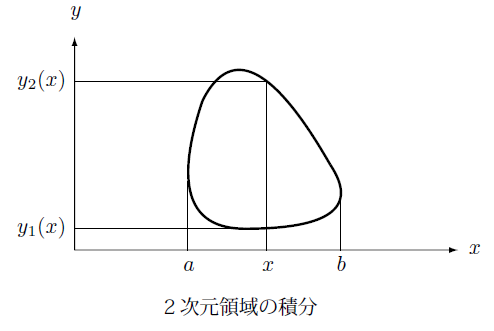
この場合は長方形の場合と違って積分範囲は積分変数によって変化します。上の図では $x$ を定めて $y$ 方向に積分する場合、積分範囲は領域の下の曲線 $y_1(x)$ から上の曲線 $y_2(x)$ となり次のように積分します。
\begin{equation}
\int_{y_1(x)}^{y_2(x)}f(x,y)dy \notag
\end{equation}
これを $x$ について積分すればこの2次元領域 $S$ の積分となります。したがって、
\begin{equation}
\int_Sf(x,y)dS=\int_a^b\int_{y_1(x)}^{y_2(x)}f(x,y)dydx \notag
\end{equation}
となります。
さて、(1.3-2)式の左辺は部分積分とガウスの発散定理を使うと次のように変形できます。
\begin{equation}
\begin{split}
&\int_S\bigl[\frac{\partial}{\partial x}\bigl(w(x,y)\epsilon\frac{\partial\phi}{\partial x}\bigr)
+\frac{\partial}{\partial y}\bigl(w(x,y)\epsilon\frac{\partial\phi}{\partial y}\bigr)\bigr]dS
-\int_S\bigl[\frac{\partial w}{\partial x}\epsilon\frac{\partial \phi}{\partial x}
+\frac{\partial w}{\partial y}\epsilon\frac{\partial \phi}{\partial y}\bigr]dS \\
&=\oint\bigl[\bigl(w(x,y)\epsilon\frac{\partial\phi}{\partial x}\bigr)n_x
+\bigl(w(x,y)\epsilon\frac{\partial\phi}{\partial y}\bigr)n_y\bigr]dl
-\int_S\bigl[\frac{\partial w}{\partial x}\epsilon\frac{\partial \phi}{\partial x}
+\frac{\partial w}{\partial y}\epsilon\frac{\partial \phi}{\partial y}\bigr]dS \\
&=\oint w(x,y)\epsilon(\boldsymbol{\nabla}\phi\cdot\boldsymbol{n})dl
-\int_S\bigl(\frac{\partial w}{\partial x}\epsilon\frac{\partial \phi}{\partial x}
+\frac{\partial w}{\partial y}\epsilon\frac{\partial \phi}{\partial y}\bigr)dS
\end{split} \notag
\end{equation}
この右辺第1項は解析領域 $S$ の境界についての周回積分で $\boldsymbol{n}$ はこの境界線に外向きにとった単位法線ベクトルです。
境界上で電場の法線成分がゼロであったらこの積分は消えます。また、境界上でポテンシャルの値が定まっている場合もこの積分は考える必要がありません。今後これらの条件がみたされるとしてこの項は無視します。
これより(1.3-2)式は次のようになります。
\begin{equation}
\int_S\bigl(\frac{\partial w}{\partial x}\epsilon\frac{\partial \phi}{\partial x}
+\frac{\partial w}{\partial y}\epsilon\frac{\partial \phi}{\partial y}\bigr)dS
=\int_Sw(x,y)\rho dS \tag*{$(1.3-3)$}
\end{equation}
これを解くために解析領域を小領域つまり有限要素に分割し、要素内のポテンシャルは要素を構成する節点での値から内挿します。
このように領域を分割したとき上の積分も要素ごとの積分の和として表わすことが出来ます。
\begin{equation}
\sum_n\int_{S_n}\bigl(\frac{\partial w}{\partial x}\epsilon\frac{\partial \phi}{\partial x}
+\frac{\partial w}{\partial y}\epsilon\frac{\partial \phi}{\partial y}\bigr)dS
=\sum_n\int_{S_n}w(x,y)\rho dS \tag*{$(1.3-4)$}
\end{equation}
ここに $S_n$ は $n$ 番目の要素が占める領域です。
1次元の場合要素は数直線上の区間で表現していましたが、2次元の場合要素の形状としてはいくつか考えられます。
よく使われる要素としては三角形要素、四角形要素などがありますが、具体的な要素の表現は後で説明するとしてそれぞれの要素タイプにはそれに応じた補間関数があり要素内のポテンシャルや任意関数 $w(x,y)$ を次のように補間します。
\begin{equation}
\begin{split}
&\phi(x,y)=\sum_\alpha N_\alpha(x,y)\phi^\alpha \\
&w(x,y)=\sum_\alpha N_\alpha(x,y)w^\alpha
\end{split} \tag*{$(1.3-5)$}
\end{equation}
ここで $\alpha$ は要素を構成する要素ごとのローカルな節点番号で $N_\alpha$ はこの節点に対応する補間関数です。また和はこの節点の数だけについてとります。
これを上の式に代入すると左辺と右辺は次のようになります。
\begin{equation}
\begin{split}
&\sum_n\sum_{\alpha\beta}w^{n\alpha}\int_{S_n}\bigl(\frac{\partial N_\alpha}{\partial x}\epsilon\frac{\partial N_\beta}{\partial x}
+\frac{\partial N_\alpha}{\partial y}\epsilon\frac{\partial N_\beta}{\partial y}\bigr)dS\phi^{n\beta} \\
&\sum_n\sum_\alpha w^{n\alpha}\int_{S_n}N_\alpha\rho dS
\end{split} \notag
\end{equation}
ここでポテンシャルや関数 $w$ の肩についている添字 $n\alpha$ などは $n$ 番目の要素の $\alpha$ 番目の節点を表しています。
ここで次の要素行列と要素ベクトルを定義します。
\begin{equation}
\begin{split}
&K_{\alpha\beta}^{(n)}=\int_{S_n}\bigl(\frac{\partial N_\alpha}{\partial x}\epsilon\frac{\partial N_\beta}{\partial x}
+\frac{\partial N_\alpha}{\partial y}\epsilon\frac{\partial N_\beta}{\partial y}\bigr)dS \\
&F_\alpha^{(n)}=\int_{S_n}N_\alpha\rho dS
\end{split} \tag*{$(1.3-6)$}
\end{equation}
これより(1.3-4)式は、
\begin{equation}
\sum_n\sum_{\alpha\beta}w^{n\alpha}K_{\alpha\beta}^{(n)}\phi^{n\beta}=\sum_n\sum_\alpha w^{n\alpha}F_\alpha^{(n)} \notag
\end{equation}
となりますが関数 $w$ でまとめると次のようになります。
\begin{equation}
\sum_n\sum_{\alpha\beta}w^{n\alpha}\bigl(K_{\alpha\beta}^{(n)}\phi^{n\beta}-F_\alpha^{(n)}\bigr)=0 \tag*{$(1.3-7)$}
\end{equation}
先ほども言ったようにここで $w^{(n\alpha)}$ や $\phi^{(n\beta)}$ は $n$ 番目の要素のローカルな節点番号 $\alpha$、$\beta$ によって表現されているのですが、一つの節点が隣り合った要素で共有される場合この番号が異なっていても同じ節点である場合があります。
そこでここで付けられた(要素番号、ローカルな節点番号)をグローバルな節点番号 $I$、$J$ などに書き換えてまとめなおすと上の式は次のようにかけます。
\begin{equation}
\sum_Iw^I(\sum_JK_{IJ}\phi^J-F_I)=0 \notag
\end{equation}
ここで $w^I$ は任意関数を離散化したものなので、どのような値であってもこの式が成立するためにはその係数がゼロである必要があります。
これよりポテンシャルの節点値に対する次の連立方程式が得られます。
\begin{equation}
\sum_JK_{IJ}\phi^J=F_I \tag*{$(1.3-8)$}
\end{equation}
ここで出てきた行列やベクトルは節点数の数だけの次元を持っています。これらを要素行列、要素ベクトルに対して全体の係数行列、ベクトルとよぶことにします。
1次元の場合は、まず要素ごとに要素行列や要素ベクトルを求めてからこれらを足しこむことによって全体の係数行列やベクトルを求めることが出来ました。
2次元の場合もこのような方法で全体行列や全体ベクトルを求めることが出来ます。
三角形要素を例に説明します。三角形要素は下の図に示すように3個の節点からできており要素内のポテンシャルは(1.3-5)式のように補間されます。
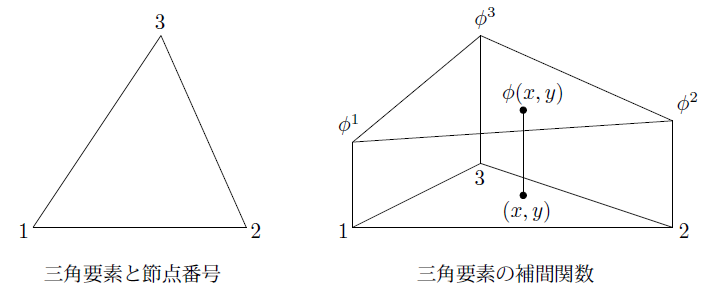
この場合補間関数は次のように求めることができます。まず3点の節点のポテンシャル値によって決まるので一次関数として表すことができます。
\begin{equation}
\phi(x,y)=ax+by+c \tag*{$(1.3-9)$}
\end{equation}
ここに、$a$、$b$、$c$ は定数であり、3点の節点 $(x_1,y_1)$、$(x_2,y_2)$、$(x_3,y_3)$ に対応するスカラーポテンシャルの値 $\phi^1$、$\phi^2$、$\phi^3$ から決めることができます。
\begin{equation}
\begin{split}
&ax_1+by_1+c=\phi^1 \\
&ax_2+by_2+c=\phi^2 \\
&ax_3+by_3+c=\phi^3
\end{split} \notag
\end{equation}
この連立方程式を解いて係数を求めると次のようになります。
\begin{equation}
\begin{bmatrix}
a \\
b \\
c
\end{bmatrix}
=\frac{1}{\Delta}
\begin{bmatrix}
y_2-y_3 & y_3-y_1 & y_1-y_2 \\
x_3-x_2 & x_1-x_3 & x_2-x_1 \\
x_2y_3-x_3y_2 & x_3y_1-x_1y_3 & x_1y_2-x_2y_1
\end{bmatrix}
\begin{bmatrix}
\phi^1 \\
\phi^2 \\
\phi^3
\end{bmatrix} \tag*{$(1.3-10)$}
\end{equation}
\begin{equation}
\Delta=(x_2y_3-x_3y_2)+(x_3y_1-x_1y_3)+(x_1y_2-x_2y_1) \tag*{$(1.3-11)$}
\end{equation}
ここで、$x_2y_3-x_3y_2$、$x_3y_1-x_1y_3$、$x_1y_2-x_2y_1$ はすこし複雑な形をしているように思われますが次のような幾何学的な意味を持っています。
各節点の位置ベクトル、
\begin{equation}
\begin{split}
&\boldsymbol{r}_1=(x_1,y_1) \\
&\boldsymbol{r}_2=(x_2,y_2) \\
&\boldsymbol{r}_3=(x_3,y_3)
\end{split} \notag
\end{equation}
とおけば、上に示したものはこれら位置ベクトルどうしの外積の $z$ 成分であることが分かります。
\begin{equation}
\begin{split}
&[\boldsymbol{r}_2\times\boldsymbol{r}_3]_z=x_2y_3-x_3y_2 \\
&[\boldsymbol{r}_3\times\boldsymbol{r}_1]_z=x_3y_1-x_1y_3 \\
&[\boldsymbol{r}_1\times\boldsymbol{r}_2]_z=x_1y_2-x_2y_1
\end{split} \tag*{$(1.3-12)$}
\end{equation}
これらの関係を下の図に示しました。
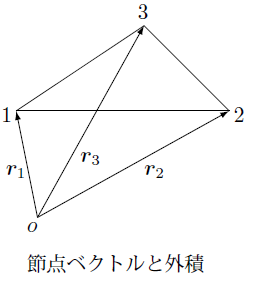
この図から $[\boldsymbol{r}_2\times\boldsymbol{r}_3]_z$ は原点 $o$ から作られる三角形 $o23$ の面積の2倍であることが分かります。
同様にして、$[\boldsymbol{r}_3\times\boldsymbol{r}_1]$ は三角形 $o31$ の面積の2倍、$[\boldsymbol{r}_1\times\boldsymbol{r}_2]_z$ は三角形$o12$の面積の2倍となります。
この図では、最初の二つの外積が正であるのに対して最後の $[\boldsymbol{r}_1\times\boldsymbol{r}_2]_z$ は負となります。
したがってこれらの和が結果的にこの要素である三角形 $123$ の面積 $S$ の2倍であることになります。
\begin{equation}
\Delta=2S \tag*{$(1.3-13)$}
\end{equation}
ここで求まった係数を使うと(1.3-9)式の要素内のポテンシャルは次のように補間されます。
\begin{equation}
\begin{split}
\phi(x,y)&=\frac{1}{\Delta}\bigl((y_2-y_3)x+(x_3-x_2)y+x_2y_3-x_3y_2\bigr)\phi^1 \\
&+\frac{1}{\Delta}\bigl((y_3-y_1)x+(x_1-x_3)y+x_3y_1-x_1y_3\bigr)\phi^2 \\
&+\frac{1}{\Delta}\bigl((y_1-y_2)x+(x_2-x_1)y+x_1y_2-x_2y_1\bigr)\phi^3 \\
&=\frac{1}{\Delta}\bigl((x_2-x)(y_3-y)-(x_3-x)(y_2-y)\bigr)\phi^1 \\
&+\frac{1}{\Delta}\bigl((x_3-x)(y_1-y)-(x_1-x)(y_3-y)\bigr)\phi^2 \\
&+\frac{1}{\Delta}\bigl((x_1-x)(y_2-y)-(x_2-x)(y_1-y)\bigr)\phi^3
\end{split} \notag
\end{equation}
これより補間関数は次のようになります。
\begin{equation}
\begin{split}
&N_1(x,y)=\frac{1}{\Delta}\bigl((x_2-x)(y_3-y)-(x_3-x)(y_2-y)\bigr) \\
&N_2(x,y)=\frac{1}{\Delta}\bigl((x_3-x)(y_1-y)-(x_1-x)(y_3-y)\bigr) \\
&N_3(x,y)=\frac{1}{\Delta}\bigl((x_1-x)(y_2-y)-(x_2-x)(y_1-y)\bigr)
\end{split} \tag*{$(1.3-14)$}
\end{equation}
ここで点 $(x,y)$ の位置ベクトルを $\boldsymbol{p}$ とおくと、
\begin{equation}
\begin{split}
&[(\boldsymbol{r}_2-\boldsymbol{p})\times(\boldsymbol{r}_3-\boldsymbol{p})]_z=(x_2-x)(y_3-y)-(x_3-x)(y_2-y) \\
&[(\boldsymbol{r}_3-\boldsymbol{p})\times(\boldsymbol{r}_1-\boldsymbol{p})]_z=(x_3-x)(y_1-y)-(x_1-x)(y_3-y) \\
&[(\boldsymbol{r}_1-\boldsymbol{p})\times(\boldsymbol{r}_2-\boldsymbol{p})]_z=(x_1-x)(y_2-y)-(x_2-x)(y_1-y)
\end{split} \notag
\end{equation}
となりますが、これらは上の補間関数の右辺のカッコ内と同じ形をしています。
これは下の図から点 $\boldsymbol{p}$ と各節点から構成される三角形の面積の2倍であることがわかります。
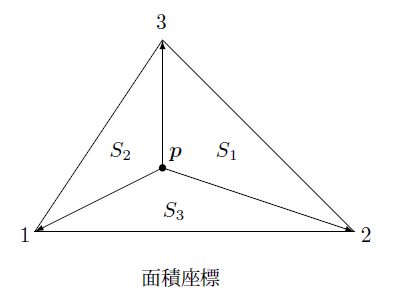
これより三角形要素の補間関数は次のようにかくことが出来ます。
\begin{equation}
\begin{split}
&N_1(x,y)=\frac{1}{2S}[(\boldsymbol{r}_2-\boldsymbol{p})\times(\boldsymbol{r}_3-\boldsymbol{p})]_z=\frac{S_1}{S} \\
&N_2(x,y)=\frac{1}{2S}[(\boldsymbol{r}_3-\boldsymbol{p})\times(\boldsymbol{r}_1-\boldsymbol{p})]_z=\frac{S_2}{S} \\
&N_3(x,y)=\frac{1}{2S}[(\boldsymbol{r}_1-\boldsymbol{p})\times(\boldsymbol{r}_2-\boldsymbol{p})]_z=\frac{S_3}{S}
\end{split} \tag*{$(1.3-15)$}
\end{equation}
ここで三角形の面積 $S_1$、$S_2$、$S_3$ を変数とみて面積座標とよぶことがあります。
例えば、点 $\boldsymbol{p}$ が節点 $1$ に一致した場合は $N_1=1$ となり他はゼロとなります。
三角形要素の補間関数が求まったので(1.3-6)式の要素行列と要素ベクトルを計算することが出来ます。
まず補間関数の微分は、
\begin{equation}
\begin{split}
&\frac{\partial N_1}{\partial x}=\frac{1}{2S}(y_2-y_3) \hspace{10mm}
\frac{\partial N_2}{\partial x}=\frac{1}{2S}(y_3-y_1) \hspace{10mm}
\frac{\partial N_3}{\partial x}=\frac{1}{2S}(y_1-y_2) \\
&\frac{\partial N_1}{\partial y}=-\frac{1}{2S}(x_2-x_3) \hspace{7mm}
\frac{\partial N_2}{\partial y}=-\frac{1}{2S}(x_3-x_1) \hspace{7mm}
\frac{\partial N_3}{\partial y}=-\frac{1}{2S}(x_1-x_2)
\end{split} \tag*{$(1.3-16)$}
\end{equation}
となります。これを使うと要素内で誘電率が一定とすれば要素行列は次のようになります。
\begin{equation}
\begin{split}
&K_{11}=\frac{\epsilon}{4S}\bigl[(y_2-y_3)^2+(x_2-x_3)^2\bigr] \\
&K_{12}=K_{21}=\frac{\epsilon}{4S}\bigl[(y_2-y_3)(y_3-y_1)+(x_2-x_3)(x_3-x_1)\bigr] \\
&K_{13}=K_{31}=\frac{\epsilon}{4S}\bigl[(y_2-y_3)(y_1-y_2)+(x_2-x_3)(x_1-x_2)\bigr] \\
&K_{22}=\frac{\epsilon}{4S}\bigl[(y_3-y_1)^2+(x_3-x_1)^2\bigr] \\
&K_{23}=K_{32}=\frac{\epsilon}{4S}\bigl[(y_3-y_1)(y_1-y_2)+(x_3-x_1)(x_1-x_2)\bigr] \\
&K_{33}=\frac{\epsilon}{4S}\bigl[(y_1-y_2)^2+(x_1-x_2)^2\bigr]
\end{split} \tag*{$(1.3-17)$}
\end{equation}
次に行列ベクトルですが、(1.3-6)式より要素内で電荷密度が一定とすれば、
\begin{equation}
F_\alpha=\rho\int N_\alpha dS=\rho\int\frac{S_\alpha(x,y)}{S}dS \notag
\end{equation}
となります。ここで要素の面積 $S$ は一定なのでこれを計算するには次の積分を行う必要があります。
\begin{equation}
\int S_\alpha(x,y)dS \notag
\end{equation}
具体的な計算を行うためにここでは $S_1$ の積分を行います。積分を行うとき、座標系はどのようにとってもよいので、ここでは節点1の対辺と垂直になる方向を $x$ 軸にとります。そうすると上の積分は、
\begin{equation}
\int_{x_1}^{x_2}\Bigl(\int_{y_a(x)}^{y_b(x)}S_1(x,y)dy\Bigr)dx \notag
\end{equation}
となります。
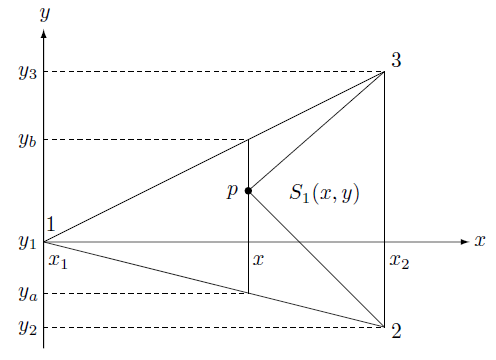
$y$ での積分は図の点 $p$ を $x$ を固定して $y_a$ から $y_b$ まで動かせて行います。このとき $S_1(x,y)$ は高さが一定の三角形の面積なので一定の値となり次のようにかけます。
\begin{equation}
S_1(x,y)=\frac{1}{2}(y_3-y_2)(x_2-x) \notag
\end{equation}
したがってこの $y$ での積分はこれに、
\begin{equation}
y_b-y_a=(y_3-y_2)\frac{x-x_1}{x_2-x_1} \notag
\end{equation}
をかけたものとなります。
\begin{equation}
\begin{split}
\int_{y_a(x)}^{y_b(x)}S_1(x,y)dy&=\frac{1}{2}(y_3-y_2)(x2-x)\times(y_3-y_2)\frac{x-x_1}{x_2-x_1} \\
&=-\frac{1}{2}\frac{(y_3-y_2)^2}{x_2-x_1}(x-x_1)(x-x_2)
\end{split} \notag
\end{equation}
したがって、
\begin{equation}
\begin{split}
\int S_1dS&=-\frac{1}{2}\frac{(y_3-y_2)^2}{x_2-x_1}\int_{x_1}^{x_2}(x-x_1)(x-x_2)dx \\
&=-\frac{1}{2}\frac{(y_3-y_2)^2}{x_2-x_1}\Bigl[\frac{1}{3}x^3-\frac{1}{2}(x_1+x_2)x^2+x_1x_2x\Bigr]_{x_1}^{x_2} \\
&=-\frac{1}{2}(y_3-y_2)^2\bigl\{\frac{1}{3}({x_1}^2+x_1x_2+{x_2}^2)-\frac{1}{2}(x_1+x_2)^2+x_1x_2\bigr\} \\
&=\frac{1}{12}(y_3-y_2)^2(x_2-x_1)^2
\end{split} \notag
\end{equation}
ですが、
\begin{equation}
S=\frac{1}{2}(y_3-y_2)(x_2-x_1) \notag
\end{equation}
なので次のようになります。
\begin{equation}
\int S_1dS=\frac{1}{3}S^2 \notag
\end{equation}
これより、
\begin{equation}
F_1=\rho\frac{1}{3}S \notag
\end{equation}
となります。他の2節点に対しても同じようにしてこれと同じ結果が得られます。
したがって要素ベクトルは次のようになります。
\begin{equation}
\begin{split}
&F_1=\frac{\rho}{3}S \\
&F_2=\frac{\rho}{3}S \\
&F_3=\frac{\rho}{3}S
\end{split} \tag*{$(1.3-18)$}
\end{equation}
簡単な例として一片の長さが $a$ の正方形領域に一定の電荷密度 $\rho$ が分布している場合を考えます。
境界条件としては図のように座標軸上でポテンシャル $\phi$ がゼロであり他の境界では電場の法線成分がゼロとします。

この領域を下の図のように18個の要素に分割します。節点数は16になります。
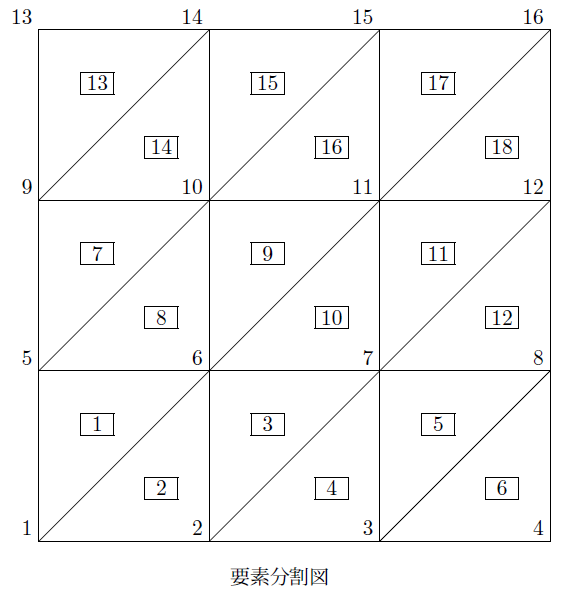
図を見てわかるように要素番号が奇数の要素はすべて同じ形状であり、偶数の要素もすべて同じ形をしています。
要素行列は(1.3-17)式からわかるように座標の差だけによって決まるので同じ形状の要素の要素行列は同じになります。
これらのローカルな節点番号を下の図のようにつけます。
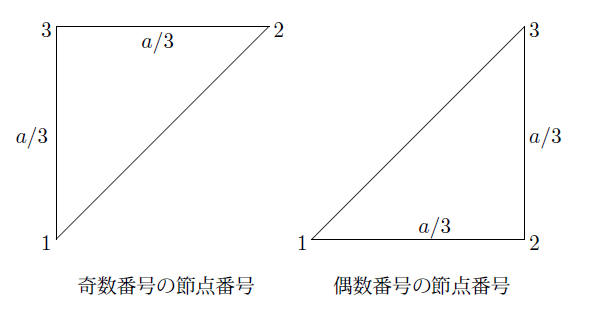
これに基づいて要素行列を計算すると、まず奇数番号の要素の場合は、$S=(a/3)^2/2$ なので、
\begin{equation}
\begin{split}
&K_{11}=\frac{\epsilon}{4S}\bigl(\frac{a}{3})^2=\frac{\epsilon}{2} \\
&K_{12}=K_{21}=0 \\
&K_{13}=K_{31}=\frac{\epsilon}{4S}\bigl(\frac{a}{3})^2=-\frac{\epsilon}{2} \\
&K_{22}=\frac{\epsilon}{4S}\bigl(\frac{a}{3})^2=\frac{\epsilon}{2} \\
&K_{23}=\frac{\epsilon}{4S}\bigl(\frac{a}{3})^2=-\frac{\epsilon}{2} \\
&K_{33}=2\frac{\epsilon}{4S}\bigl(\frac{a}{3})^2=2\frac{\epsilon}{2}
\end{split} \notag
\end{equation}
となるので、まとめてかくと次のようになります。
\begin{equation}
K=\frac{\epsilon}{2}
\begin{bmatrix}
1 & 0 & -1 \\
0 & 1 & -1 \\
-1 & -1 & 2
\end{bmatrix} \tag*{$(1.3-19)$}
\end{equation}
偶数番号の要素については、
\begin{equation}
\begin{split}
&K_{11}=\frac{\epsilon}{4S}\bigl(\frac{a}{3})^2=\frac{\epsilon}{2} \\
&K_{12}=K_{21}=-\frac{\epsilon}{4S}\bigl(\frac{a}{3})^2=-\frac{\epsilon}{2} \\
&K_{13}=K_{31}=0 \\
&K_{22}=2\frac{\epsilon}{4S}\bigl(\frac{a}{3})^2=2\frac{\epsilon}{2} \\
&K_{23}=-\frac{\epsilon}{4S}\bigl(\frac{a}{3})^2=-\frac{\epsilon}{2} \\
&K_{33}=\frac{\epsilon}{4S}\bigl(\frac{a}{3})^2=\frac{\epsilon}{2}
\end{split} \notag
\end{equation}
なので、
\begin{equation}
K=\frac{\epsilon}{2}
\begin{bmatrix}
1 & -1 & 0 \\
-1 & 2 & -1 \\
0 & -1 & 1
\end{bmatrix} \tag*{$(1.3-20)$}
\end{equation}
となります。
要素行列は(1.3-18)式より次のようになります。
\begin{equation}
F=\frac{\rho a^2}{54}
\begin{bmatrix}
1 \\
1 \\
1
\end{bmatrix} \tag*{$(1.3-21)$}
\end{equation}
要素行列と要素ベクトルが求まったのでつぎはこれから全体の係数行列とベクトルを求めます。
要素番号 $1$ の場合ローカルな節点番号と節点番号とは次の関係にあります。
\begin{equation}
1\rightarrow 1 \hspace{10mm} 2\rightarrow 6 \hspace{10mm} 3\rightarrow 5 \notag
\end{equation}
これよりこの要素行列を $K^{(1)}_{ij}$ とかくと、全体の係数行列に対して次のように代入します。
\begin{equation}
\begin{split}
&K_{11}=K^{(1)}_{11} \hspace{10mm} K_{16}=K^{(1)}_{12} \hspace{10mm} K_{15}=K^{(1)}_{13} \\
&K_{61}=K^{(1)}_{21} \hspace{10mm} K_{66}=K^{(1)}_{22} \hspace{10mm} K_{65}=K^{(1)}_{23} \\
&K_{56}=K^{(1)}_{31} \hspace{10mm} K_{56}=K^{(1)}_{32} \hspace{10mm} K_{55}=K^{(1)}_{33}
\end{split} \notag
\end{equation}
同様に、要素番号 $2$ の場合ローカルな節点番号と節点番号の関係は、
\begin{equation}
1\rightarrow 1 \hspace{10mm} 2\rightarrow 2 \hspace{10mm} 3\rightarrow 6 \notag
\end{equation}
となり、この要素行列と全体の係数行列に対して次のように代入します。
\begin{equation}
\begin{split}
&K_{11}=K^{(2)}_{11} \hspace{10mm} K_{12}=K^{(2)}_{12} \hspace{10mm} K_{16}=K^{(2)}_{13} \\
&K_{21}=K^{(2)}_{21} \hspace{10mm} K_{22}=K^{(2)}_{22} \hspace{10mm} K_{26}=K^{(2)}_{23} \\
&K_{61}=K^{(2)}_{31} \hspace{10mm} K_{62}=K^{(2)}_{32} \hspace{10mm} K_{66}=K^{(2)}_{33}
\end{split} \notag
\end{equation}
全ての要素についての要素行列を求めて下の図のように全体の係数行列の対応する番号に足しこみます。
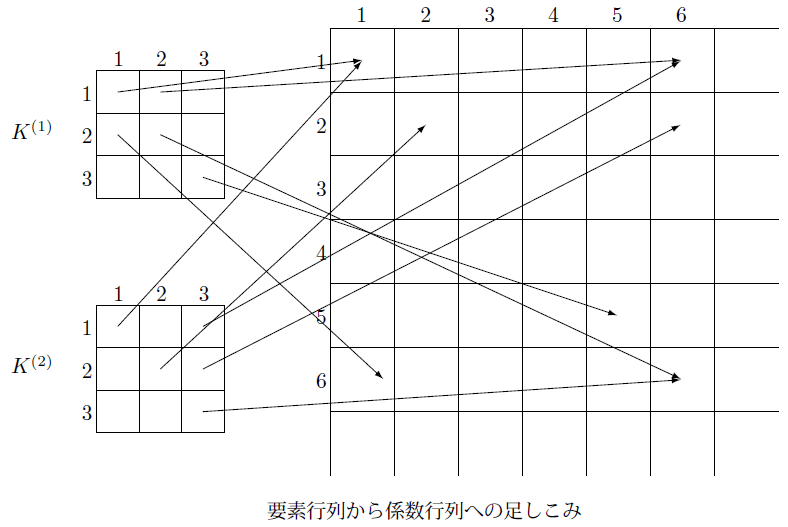
この図では見やすくするため一部だけ表示しています。
その結果次の係数行列が得られます。
\begin{equation}
K=\frac{\epsilon}{2}
\begin{bmatrix}
2 & -1 & 0 & 0 & -1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\
-1 & 4 & -1 & 0 & 0 & -2 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\
0 & -1 & 4 & -1 & 0 & 0 & -2 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\
0 & 0 & -1 & 2 & 0 & 0 & 0 & -1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\
-1 & 0 & 0 & 0 & 4 & -2 & 0 & 0 & -1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\
0 & -2 & 0 & 0 & -2 & 8 & -2 & 0 & 0 & -2 & 0 & 0 & 0 & 0 & 0 & 0 \\
0 & 0 & -2 & 0 & 0 & -2 & 8 & -2 & 0 & 0 & -2 & 0 & 0 & 0 & 0 & 0 \\
0 & 0 & 0 & -1 & 0 & 0 & -2 & 4 & 0 & 0 & 0 & -1 & 0 & 0 & 0 & 0 \\
0 & 0 & 0 & 0 & -1 & 0 & 0 & 0 & 4 & -2 & 0 & 0 & -1 & 0 & 0 & 0 \\
0 & 0 & 0 & 0 & 0 & -2 & 0 & 0 & -2 & 8 & -2 & 0 & 0 & -2 & 0 & 0 \\
0 & 0 & 0 & 0 & 0 & 0 & -2 & 0 & 0 & -2 & 8 & -2 & 0 & 0 & -2 & 0 \\
0 & 0 & 0 & 0 & 0 & 0 & 0 & -1 & 0 & 0 & -2 & 4 & 0 & 0 & 0 & -1 \\
0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & -1 & 0 & 0 & 0 & 2 & -1 & 0 & 0 \\
0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & -2 & 0 & 0 & -1 & 4 & -1 & 0 \\
0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & -2 & 0 & 0 & -1 & 4 & -1 \\
0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & -1 & 0 & 0 & -1 & 2
\end{bmatrix}
\hspace{2mm} F=\frac{\rho a^2}{54}
\begin{bmatrix}
2 \\
3 \\
3 \\
1 \\
3 \\
6 \\
6 \\
3 \\
3 \\
6 \\
6 \\
3 \\
1 \\
3 \\
3 \\
2
\end{bmatrix} \tag*{$(1.3-22)$}
\end{equation}
この係数行列を見るとまず対称行列、すなわち行番号と列番号を入れ替えても同じであることが分かります。
\begin{equation}
K_{ij}=K_{ji} \notag
\end{equation}
またゼロでない行列要素が対角項の付近に帯状に分布しておりゼロが結構多いことが分かります。
次に境界条件を考える必要があります。
この問題では、ポテンシャルがゼロである境界と電場も法線成分がゼロである境界があります。
ポテンシャルが指定されている境界条件はディレクレ境界条件または第1種境界条件とよばれます。
また、電場の法線成分つまりポテンシャルの法線方向の勾配が指定される境界条件はノイマン境界条件または第2種境界条件とよんでいます。
ノイマン境界条件は基礎方程式である(1.3-3)式を導く際、境界積分をゼロにしましたのでこの場合自動的に満たされています。
ポテンシャルがゼロの節点番号は、$1$、$2$、$3$、$4$、$5$、$9$、$13$ ですから、
\begin{equation}
\phi_1=\phi_2=\phi_3=\phi_4=\phi_5=\phi_9=\phi_{13}=0 \notag
\end{equation}
です。この条件を考慮するためには連立方程式のこの番号に対する行と列を除いてやればよいことが分かっています。
これに関しては連立方程式の拘束条件として改めて議論します。
この番号の行と列を除いた連立方程式は次のようになります。
\begin{equation}
\frac{\epsilon}{2}
\begin{bmatrix}
8 & -2 & 0 & -2 & 0 & 0 & 0 & 0 & 0 \\
-2 & 8 & -2 & 0 & -2 & 0 & 0 & 0 & 0 \\
0 & -2 & 4 & 0 & 0 & -1 & 0 & 0 & 0 \\
-2 & 0 & 0 & 8 & -2 & 0 & -2 & 0 & 0 \\
0 & -2 & 0 & -2 & 8 & -2 & 0 & -2 & 0 \\
0 & 0 & -1 & 0 & -2 & 4 & 0 & 0 & -1 \\
0 & 0 & 0 & -2 & 0 & 0 & 4 & -1 & 0 \\
0 & 0 & 0 & 0 & -2 & 0 & -1 & 4 & -1 \\
0 & 0 & 0 & 0 & 0 & -1 & 0 & -1 & 2
\end{bmatrix}
\begin{bmatrix}
\phi_6 \\
\phi_7 \\
\phi_8 \\
\phi_{10} \\
\phi_{11} \\
\phi_{12} \\
\phi_{14} \\
\phi_{15} \\
\phi_{16}
\end{bmatrix}
=\frac{\rho a^2}{54}
\begin{bmatrix}
6 \\
6 \\
3 \\
6 \\
6 \\
3 \\
3 \\
3 \\
2
\end{bmatrix} \tag*{$(1.3-23)$}
\end{equation}
ここで、
\begin{equation}
\frac{\rho a^2}{27\epsilon}=1 \tag*{$(1.3-24)$}
\end{equation}
としてこれを解くと結果は次のようになります。
\begin{equation}
\begin{split}
&\phi_{13}=0 \hspace{5mm} \phi_{14}=4.692308 \hspace{6mm} \phi_{15}=7.230769 \hspace{5mm} \phi_{16}=8.230769 \\
&\phi_{09}=0 \hspace{5mm} \phi_{10}=4.269231 \hspace{6mm} \phi_{11}=6.5 \hspace{19mm} \phi_{12}=7.230769 \\
&\phi_{05}=0 \hspace{5mm} \phi_{06}=2.884615 \hspace{6mm} \phi_{07}=4.269231 \hspace{5mm} \phi_{08}=4.692308 \\
&\phi_{01}=0 \hspace{5mm} \phi_{02}=0 \hspace{24mm} \phi_{03}=0 \hspace{24mm} \phi_{04}=0
\end{split} \tag*{$(1.3-25)$}
\end{equation}
要素分割図と対応できるように表示しています。
(1.3-24)式をみたさない場合は、これに(1.3-24)式の左辺をかけたものがポテンシャルの値となります。
これまで電場の2次元において三角形要素を使った有限要素法をかなり詳しく説明してきました。これによって電場の基礎方程式をどのように有限要素に分割し、ポテンシャルを節点の持つ有限個のポテンシャル値から要素内のポテンシャルを内挿し、そのポテンシャルが基礎方程式をみたすようにこれら節点におけるポテンシャルの値を求める連立方程式をどのように作成するのかということがかなり具体的にわかっていただけたと思います。
2次元の要素分割に使う要素としては三角形要素だけではなく四角形要素もよく使われますので次にその話をします。
有限要素法では場の方程式を解析する領域で有限要素に分割し、要素内で場を内挿して表現します。このとき電場のポテンシャルなどの場は連続に分布していると考えていますので、有限要素に分割したとき要素境界で不連続になることは避けなければなりません。
したがって隣り合う要素が共有する境界で補間関数が連続となるようなものを使う必要があります。一次元の場合は境界は点となるのでそこで連続にすることは簡単でした。また今まで述べてきた三角形要素は一次の補間関数を使っていたので要素境界で不連続になることはありません。
ところが四角形要素の場合一次より高次の補間関数となるので要素境界で連続となるとは限りません。
まず境界で連続となる補間関数を持つ正方形要素から出発します。
下の図のように四つの頂点に節点を置き番号を付けます。
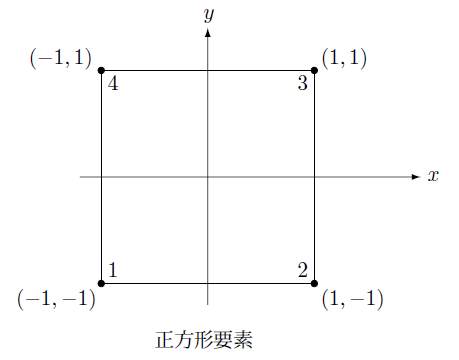
この正方形要素内の補間関数として次のようなものを考えます。
\begin{equation}
\begin{split}
&N_1(x,y)=\frac{1}{4}(1-x)(1-y) \\
&N_2(x,y)=\frac{1}{4}(1+x)(1-y) \\
&N_3(x,y)=\frac{1}{4}(1+x)(1+y) \\
&N_4(x,y)=\frac{1}{4}(1-x)(1+y) \\
\end{split} \tag*{$(1.3-26)$}
\end{equation}
この補間関数を使って要素内の点におけるポテンシャル $\phi$ などを次のように補間します。
\begin{equation}
\phi(x,y)=\sum_{\alpha=1}^4N_\alpha(x,y)\phi^\alpha \tag*{$(1.3-27)$}
\end{equation}
この補間関数から補間する点が節点と一致したときはポテンシャルの値がその節点値となることが分かります。
この要素は一片の長さが $2$ で中心が原点に位置しています。したがって要素がこれ以外の大きさや位置の場合はこの補間関数を使うことが出来ません。
ただしこの正方形を平行移動したときの補間関数はすこしの修正で補間関数を作ることが出来ます。
例えば $x$ 方向に $2$ だけ平行移動した場合は次のようになります。
\begin{equation}
\begin{split}
&N_5(x,y)=\frac{1}{4}(3-x)(1-y) \\
&N_6(x,y)=\frac{1}{4}(-1+x)(1-y) \\
&N_7(x,y)=\frac{1}{4}(-1+x)(1+y) \\
&N_8(x,y)=\frac{1}{4}(3-x)(1+y) \\
\end{split} \notag
\end{equation}
ただし節点番号は変えています。この要素と元の要素とは節点番号 $2$ と $5$、$3$ と $8$ を共有しておりこの節点の乗る境界が接しています。
したがってこの辺に乗る点 $(1,y)$ のポテンシャルは両要素で次のように補間されます。
まず最初の要素では、
\begin{equation}
\phi(1,y)=\frac{1}{2}(1-y)\phi^2+\frac{1}{2}(1+y)\phi^3 \notag
\end{equation}
となり、次に平行移動した位置にある要素では次のようになります。
\begin{equation}
\phi(1,y)=\frac{1}{2}(1-y)\phi^5+\frac{1}{2}(1+y)\phi^8 \notag
\end{equation}
ここで $\phi^2$ と $\phi^5$、$\phi^3$ と $\phi^8$ は同じ節点でありそれぞれ同じ値なのでこれらの関数は全く等しくなり、要素境界での関数の連続性が成り立っていることが分かります。
このように正方形要素は関数の連続性は満たされますが場所ごとに補間関数を変える必要があります。
ところが補間をする場合問題なのは要素の節点と補間する点の相対的な位置関係であり、節点の座標自体はどこにあってもよいはずです。
そこで、最初の要素から平行移動で移せる要素については、原点まで平行移動して補間すれば(1.3-26)式の補間関数が使えることになります。
ただし実際の節点の座標と区別するために要素中心を原点とする新しい座標系 $(r,s)$ を導入します。
すると補間関数はこの座標を使って次のように表されます。
\begin{equation}
\begin{split}
&N_1(r,s)=\frac{1}{4}(1-r)(1-s) \\
&N_2(r,s)=\frac{1}{4}(1+r)(1-s) \\
&N_3(r,s)=\frac{1}{4}(1+r)(1+s) \\
&N_4(r,s)=\frac{1}{4}(1-r)(1+s) \\
\end{split} \tag*{$(1.3-28)$}
\end{equation}
この要素の中心座標を $(x_c,y_c)$ とすれば、
\begin{equation}
\begin{split}
&r=x-x_c \\
&s=y-y_c
\end{split} \notag
\end{equation}
の関係があります。これは座標変換ですのでもっと一般的に平行移動ばかりでなく回転を考えることが出来ます。
回転を行っても最初の座標と変換した座標の関係が分かっていれば回転移動した要素に対しても同じ補間関数が使えます。
回転角を $\theta$ とすれば変換は次のようになります。
\begin{equation}
\begin{bmatrix}
r \\
s
\end{bmatrix}
=
\begin{bmatrix}
\mathrm{cos}\theta & \mathrm{sin}\theta \\
-\mathrm{sin}\theta & \mathrm{cos}\theta
\end{bmatrix}
\begin{bmatrix}
x-x_c \\
y-y_c
\end{bmatrix} \notag
\end{equation}
ここまでは一辺の長さが $2$ の正方形の形は変えないような変換を考えましたが、大きさを変えるような変換も可能です。
たとえば、
\begin{equation}
\begin{bmatrix}
r \\
s
\end{bmatrix}
=
\begin{bmatrix}
\alpha & 0 \\
0 & \beta
\end{bmatrix}
\begin{bmatrix}
x-x_c \\
y-y_c
\end{bmatrix} \notag
\end{equation}
です。もちろんこれらを組み合わせたことも考えられますのでいろんな方向を向いた大きさの異なる要素を扱うことが出来ます。
ただしこれらの変換で移行する要素は長方形ということになります。
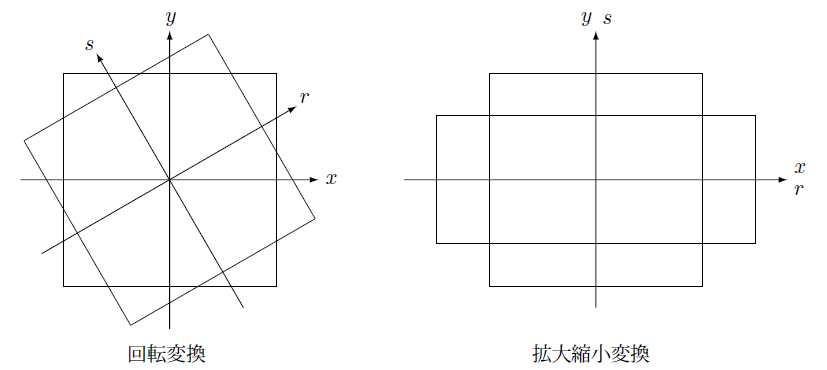
このように原点を中心とした一辺の長さが $2$ の正方形に座標変換できれば(1.3-26)式の補間関数が使えることが分かりました。
それでは一般の四角形の要素に対してはどうでしょうか。例えば下の図の左の四角形要素を右の図のように正方形になるような変換が出来れば同じ補間関数が使えます。
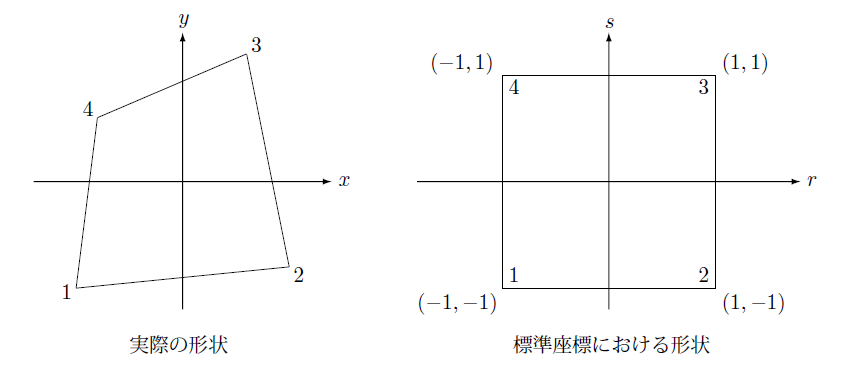
そこで考えられるのが要素内の座標を同じ補間関数を使って節点の座標から補間することです。
\begin{equation}
\begin{split}
&x=\sum_\alpha N_\alpha(r,s)x^\alpha \\
&y=\sum_\alpha N_\alpha(r,s)y^\alpha
\end{split} \tag*{$(1.3-29)$}
\end{equation}
ここで $(x^\alpha,y^\alpha)$ は節点 $\alpha$ の座標です。この補間式を、現在使っている座標 $(x.y)$ と右の図のあるような $(r,s)$ 座標との変換式と考えているのです。このような場合これらの補間関数は、要素の形状を表現するので形状関数とよばれます。
実際にはこのように形状関数が必ずしも補間関数と一致する必要はないのですが、一致した形状関数を使うことが多いので今後これを使用します。
このような要素、すなわち形状関数と補間関数が同じものを使用する場合をアイソパラメトリック要素とよんでいます。
また、この形状関数で表される要素は座標を $(r,s)$ で表した場合、要素は右の図にあるように頂点が座標 $(\pm1,\pm1)$ を持つことになりますが、この座標系を標準座標とよんでいます。
標準座標系を使って話をする場合、元の変数と異なるため微分や積分をするさい注意が必要です。要素行列や要素ベクトルを作成する場合は(1.3-6)式、
\begin{equation}
\begin{split}
&K_{\alpha\beta}^{(n)}=\int_{S_n}\bigl(\frac{\partial N_\alpha(r,s)}{\partial x}\epsilon\frac{\partial N_\beta(r,s)}{\partial x}
+\frac{\partial N_\alpha(r,s)}{\partial y}\epsilon\frac{\partial N_\beta(r,s)}{\partial y}\bigr)dS \\
&F_\alpha^{(n)}=\int_{S_n}N_\alpha(r,s)\rho dS
\end{split} \notag
\end{equation}
を計算する必要があります。ここでの表現は元の座標におけるものですが、補間関数は標準座標でかかれているので微分をとるときは次のように
変数変換を行います。
\begin{equation}
\begin{split}
&\frac{\partial N_\alpha(r,s)}{\partial x}=\frac{\partial N_\alpha(r,s)}{\partial r}\frac{\partial r}{\partial x}
+\frac{\partial N_\alpha(r,s)}{\partial s}\frac{\partial s}{\partial x} \\
&\frac{\partial N_\alpha(r,s)}{\partial y}=\frac{\partial N_\alpha(r,s)}{\partial r}\frac{\partial r}{\partial y}
+\frac{\partial N_\alpha(r,s)}{\partial s}\frac{\partial s}{\partial y}
\end{split} \tag*{$(1,3-30)$}
\end{equation}
補間関数の標準座標 $(r,s)$ での微分は(1.3-28)式から次のように計算することが出来ます。
\begin{equation}
\begin{split}
&\frac{\partial N_1}{\partial r}=-\frac{1}{4}(1-s) \hspace{10mm} \frac{\partial N_1}{\partial s}=-\frac{1}{4}(1-r) \\
&\frac{\partial N_2}{\partial r}=+\frac{1}{4}(1-s) \hspace{10mm} \frac{\partial N_2}{\partial s}=-\frac{1}{4}(1+r) \\
&\frac{\partial N_3}{\partial r}=+\frac{1}{4}(1+s) \hspace{10mm} \frac{\partial N_3}{\partial s}=+\frac{1}{4}(1+r) \\
&\frac{\partial N_4}{\partial r}=-\frac{1}{4}(1+s) \hspace{10mm} \frac{\partial N_4}{\partial s}=+\frac{1}{4}(1-r)
\end{split} \tag*{$(1.3-31)$}
\end{equation}
標準座標の微分、例えば $\partial r/\partial x$ を行うには次のようにします。まず(1.3-29)式の両辺を標準座標で微分します。
\begin{equation}
\begin{split}
&\frac{\partial x}{\partial r}=\sum_\alpha\frac{\partial N_\alpha}{\partial r}x^\alpha \hspace{10mm}
\frac{\partial x}{\partial s}=\sum_\alpha\frac{\partial N_\alpha}{\partial s}x^\alpha \\
&\frac{\partial y}{\partial r}=\sum_\alpha\frac{\partial N_\alpha}{\partial r}y^\alpha \hspace{10mm}
\frac{\partial y}{\partial s}=\sum_\alpha\frac{\partial N_\alpha}{\partial s}y^\alpha \\
\end{split} \notag
\end{equation}
ところで、
\begin{equation}
\begin{split}
&\frac{\partial x}{\partial x}=\frac{\partial x}{\partial r}\frac{\partial r}{\partial x}
+ \frac{\partial x}{\partial s}\frac{\partial s}{\partial x} = 1 \hspace{10mm}
\frac{\partial x}{\partial y}=\frac{\partial x}{\partial r}\frac{\partial r}{\partial y}
+ \frac{\partial x}{\partial s}\frac{\partial s}{\partial y} = 0 \\
&\frac{\partial y}{\partial x}=\frac{\partial y}{\partial r}\frac{\partial r}{\partial x}
+ \frac{\partial y}{\partial s}\frac{\partial s}{\partial x} = 0 \hspace{10mm}
\frac{\partial y}{\partial y}=\frac{\partial y}{\partial r}\frac{\partial r}{\partial y}
+ \frac{\partial y}{\partial s}\frac{\partial s}{\partial y} = 1
\end{split} \notag
\end{equation}
です。この関係を行列でかくと次のようになります。
\begin{equation}
\begin{bmatrix}
{\partial x}/{\partial r} & {\partial x}/{\partial s} \\
{\partial y}/{\partial r} & {\partial y}/{\partial s}
\end{bmatrix}
\begin{bmatrix}
{\partial r}/{\partial x} & {\partial r}/{\partial y} \\
{\partial s}/{\partial x} & {\partial s}/{\partial y}
\end{bmatrix}
=
\begin{bmatrix}
1 & 0 \\
0 & 1
\end{bmatrix} \tag*{$(1.3-32)$}
\end{equation}
これより、標準座標 $(r,s)$ の座標 $(x,y)$ による微係数で作った行列は、座標 $(x,y)$ を標準座標で微分した行列の逆行列であることが分かります。
そこで、
\begin{equation}
D=\frac{\partial x}{\partial r}\frac{\partial y}{\partial s}-\frac{\partial x}{\partial s}\frac{\partial y}{\partial r} \tag*{$(1.3-33)$}
\end{equation}
とおけば、クラーメルの公式より、
\begin{equation}
\begin{bmatrix}
{\partial x}/{\partial r} & {\partial x}/{\partial s} \\
{\partial y}/{\partial r} & {\partial y}/{\partial s}
\end{bmatrix}^{-1}
=\frac{1}{D}
\begin{bmatrix}
{\partial y}/{\partial s} & -{\partial x}/{\partial s} \\
-{\partial y}/{\partial r} & {\partial x}/{\partial r}
\end{bmatrix} \notag
\end{equation}
となるので、標準座標の微分は次のようにかけます。
\begin{equation}
\begin{split}
&\frac{\partial r}{\partial x}=\frac{1}{D}\frac{\partial y}{\partial s}=\frac{1}{D}\sum_\alpha\frac{\partial N_\alpha}{\partial s}y^\alpha \\
&\frac{\partial r}{\partial y}=-\frac{1}{D}\frac{\partial x}{\partial s}=-\frac{1}{D}\sum_\alpha\frac{\partial N_\alpha}{\partial s}x^\alpha \\
&\frac{\partial s}{\partial x}=-\frac{1}{D}\frac{\partial y}{\partial r}=-\frac{1}{D}\sum_\alpha\frac{\partial N_\alpha}{\partial r}y^\alpha \\
&\frac{\partial s}{\partial y}=\frac{1}{D}\frac{\partial x}{\partial r}=\frac{1}{D}\sum_\alpha\frac{\partial N_\alpha}{\partial r}x^\alpha
\end{split} \tag*{$(1.3-34)$}
\end{equation}
これによって要素行列を求めるための(1.3-6)式の被積分関数を標準座標でかきかえることが出来ました。
次に標準座標での積分ですが、一般に積分は座標変換によって次のようになります。被積分関数はどちらの座標でも同じなので同じ位置で、
\begin{equation}
f(x,y)=F(r,s) \notag
\end{equation}
としたとき、
\begin{equation}
\int_Sf(x,y)dS=\int_{-1}^1\int_{-1}^1F(r,s)\Bigl|\frac{\partial(x,y)}{\partial(r,s)}\Bigr|drds \tag*{$(1.3-35)$}
\end{equation}
となります。ここに、
\begin{equation}
\frac{\partial(x,y)}{\partial(r,s)}=det
\begin{bmatrix}
{\partial x}/{\partial r} & {\partial x}/{\partial s} \\
{\partial y}/{\partial r} & {\partial y}/{\partial s}
\end{bmatrix} \tag*{$(1.3-36)$}
\end{equation}
は前に出てきた変換行列の行列式で、ヤコビアンといいます。
さて次に必要なことは(1.3-6)式の積分を実行することですが、被積分関数を標準座標にかきなおしたとはいえかなり複雑な形をしています。
また、誘電率などが要素内部で変化しているような場合この積分を計算することは難しくなります。
そこで、数値積分を行うことになるのですが、ここで少し数値積分について簡単に説明しておきます。
まず1次元積分として次の積分を考えます。
\begin{equation}
I=\int_a^bf(x)dx \tag*{$(1.3-37)$}
\end{equation}
まずこの積分を近似的に解くために積分領域である区間 $[a,b]$ をいくつかの小区間に等分割します。分割された区間長を $h$ とします。
分割された $i$ 番目の区間 $[x_i,x_{i+1}]$ で関数値が一定値 $f(x_i)$ で近似する場合この積分は次のようにかけます。
\begin{equation}
\int_a^bf(x)dx\simeq\sum_{i=1}^nf(x_i)h \tag*{$(1.3-38)$}
\end{equation}
ここに $n$ は領域の分割数です。下の図の左にはこの近似の図を示しています。
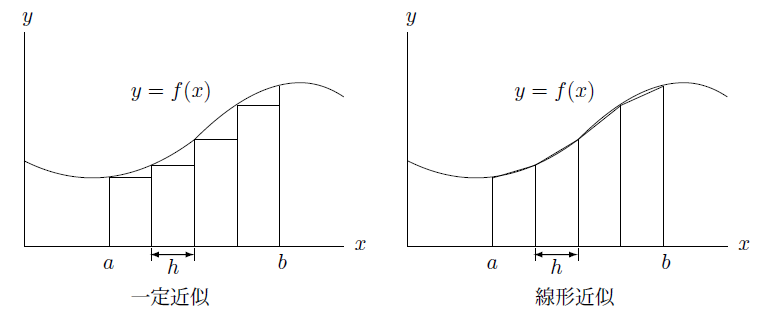
図から分かるように分割数が粗いとこの方法では誤差が大きくなります。
そこで図の右側に示したように分割された区間 $[x_i,x_{i+1}]$ で関数を線形補間して積分を近似します。
\begin{equation}
\int_{x_i}^{x_{i+1}}f(x)dx\simeq\frac{f(x_i)+f(x_{i+1})}{2}h \notag
\end{equation}
この場合積分は次のようにかけます。
\begin{equation}
\int_a^bf(x)dx\simeq \frac{1}{2}f(x_1)h+\sum_{i=2}^{n-1}f(x_i)h+\frac{1}{2}f(x_n)h \tag*{$(1.3-39)$}
\end{equation}
図を見るとこの近似の方がずいぶん精度が良くなるように思われますがこの式と(1.3-38)式を比べると区間両端の関数値の扱いだけが異なっているだけです。
この二つの場合分割された区間の両端の関数値を使ってこの区間の積分を表現しています。
もっと精度を上げるために関数をもっと高次の関数で近似するために複数個の区間の節点数値を使うという方法があります。
ここでは一つの区間内の複数の点を使ってできるだけ精度を上げる方法を考えます。
区間 $[x_i,x_{i+1}]$ における積分を次のように近似します。
\begin{equation}
\int_{x_i}^{x_{i+1}}f(x)dx\simeq\sum_gf(x_g)w_g \notag
\end{equation}
ここで $x_g$ は区間の中でいくつかの点を選び、誤差を最小にするように決まる$g$番目の座標であり、$w_g$ はその時の関数値にかける重みです。
ただこのままでは、これらの点の座標は区間の取り方によって変わるので、積分する区間が $[-1,1]$ になるように変数変換をします。
この場合は次のようになります。
\begin{equation}
\int_{-1}^1f(x)dx\simeq\sum_gf(x_g)w_g \tag*{$(1.3-40)$}
\end{equation}
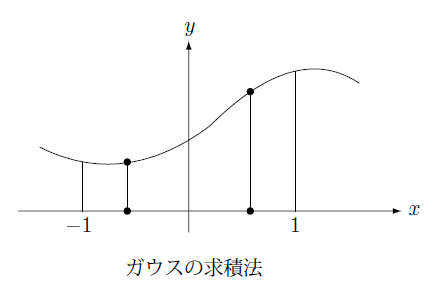
この近似法はガウスの求積法として知られており、点の数と数値積分は次のようになります。
\begin{equation}
\begin{split}
&I_1=f(0)\times 2 \\
&I_2=f(-\sqrt{\frac{1}{3}})\times 1+f(+\sqrt{\frac{1}{3}})\times 1 \\
&I_3=f(-\sqrt{\frac{3}{5}})\times\frac{5}{9}+f(0)\times\frac{8}{9}+f(+\sqrt{\frac{3}{5}})\times\frac{5}{9}
\end{split} \tag*{$(1.3-41)$}
\end{equation}
この近似は2点でもかなりの精度が出ます。ちなみに関数が3次式以下であれば誤差無しで計算できます。
それを示すために積分する関数を、
\begin{equation}
f(x)=ax^3+bx^2+cx+d \notag
\end{equation}
この積分は、
\begin{equation}
\int_{-1}^1(ax^3+bx^2+cx+d)dx=\bigl[\frac{1}{4}ax^4+\frac{1}{3}bx^3+\frac{1}{2}cx^2+dx\bigr]_{-1}^1=\frac{2}{3}b+2d \notag
\end{equation}
となりますが、ガウスの求積法では、
\begin{equation}
a\bigl(-\sqrt{\frac{1}{3}}\bigr)^3+b\bigl(-\sqrt{\frac{1}{3}}\bigr)^2+c\bigl(-\sqrt{\frac{1}{3}}\bigr)+d
+a\bigl(\sqrt{\frac{1}{3}}\bigr)^3+b\bigl(\sqrt{\frac{1}{3}}\bigr)^2+c\bigl(\sqrt{\frac{1}{3}}\bigr)+d
=\frac{2}{3}b+2d \notag
\end{equation}
となり、両者は一致します。
この方法を多重積分に拡張することは簡単です。2次元の場合は次のようになります。
\begin{equation}
\begin{split}
\int_{-1}^1\int_{-1}^1f(x,y)dxdy&=\int_{-1}^1\bigl\{\int_{-1}^1f(x,y)dx\bigr\}dy \\
&\simeq\int_{-1}^1\bigl\{\sum_if(x_i,y)w_i\bigr\}dy \\
&\simeq\sum_j\sum_if(x_i,y_j)w_iw_j
\end{split} \tag*{$(1.3-42)$}
\end{equation}
同様にして3次元の場合は、
\begin{equation}
\int_{-1}^1\int_{-1}^1\int_{-1}^1f(x,y,z)dxdydz\simeq\sum_k\sum_j\sum_if(x_i,y_j,z_k)w_iw_jw_k \tag*{$(1.3-43)$}
\end{equation}
となります。
さて、数値積分の方法が分かったのでこれで要素行列を求めることが出来ます。
要素を標準座標で表現すると(1.3-6)式の要素行列と要素ベクトルは次のようになります。
\begin{equation}
\begin{split}
&K_{\alpha\beta}^{(n)}=\int_{-1}^1\int_{-1}^1\bigl(\frac{\partial N_\alpha(r,s)}{\partial x}\epsilon\frac{\partial N_\beta(r,s)}{\partial x}
+\frac{\partial N_\alpha(r,s)}{\partial y}\epsilon\frac{\partial N_\beta(r,s)}{\partial y}\bigr)\Bigl|\frac{\partial(x,y)}{\partial(r,s)}\Bigr|drds \\
&F_\alpha^{(n)}=\int_{-1}^1\int_{-1}^1N_\alpha(r,s)\rho\Bigl|\frac{\partial(x,y)}{\partial(r,s)}\Bigr|drds
\end{split} \tag*{$(1.3-44)$}
\end{equation}
ただしこの被積分関数は(1.3-30)式以降述べたようにすべて標準座標で表現することが出来ます。したがって今後、補間関数の微分 $\partial N_\alpha/\partial x$ や、
ヤコビアンはこのようにかきますが標準座標で表現されているものとします。
また、この積分領域は数値積分のところで説明したガウスの求積法の積分範囲と同じなのでそのまま適用することが出来ます。
まず、要素行列は次のようになります。
\begin{equation}
K_{\alpha\beta}^{(n)}=\sum_i\sum_j\bigl(\frac{\partial N_\alpha(r_i,s_j)}{\partial x}\epsilon\frac{\partial N_\beta(r_i,s_j)}{\partial x}
+\frac{\partial N_\alpha(r_i,s_j)}{\partial y}\epsilon\frac{\partial N_\beta(r_i,s_j)}{\partial y}\bigr)
\Bigl|\frac{\partial(x,y)}{\partial(r,s)}\Bigr|_{(r_i,s_j)}w_{ij} \tag*{$(1.3-45)$}
\end{equation}
ここでヤコビアンと重み $w_{ij}$ は積分点での値です。
三角形要素の要素行列のときには誘電率 $\epsilon$ は要素内で一定としていましたが、数値積分を行う場合は積分点ごとに変えることもできます。
これは誘電率が電場などによって変化する非線形誘電体を扱う場合必要になってきます。
次に要素ベクトルは次のようになります。
\begin{equation}
F_\alpha^{(n)}=\sum_i\sum_jN_\alpha(r_i,s_j)\rho\Bigl|\frac{\partial(x,y)}{\partial(r,s)}\Bigr|_{(r_i,s_j)}w_{ij} \tag*{$(1.3-46)$}
\end{equation}
ここでは電荷密度も誘電率と同じように要素内で場所ごとに変化してもかまいません。
このようにしてすべての要素について要素行列と要素ベクトルができると、これから全体の係数行列とベクトルを構成することが出来ます。
要素内部では節点についてローカルな番号 $\alpha$、$\beta$ を付けて表現してきたのですが、例えば要素番号 $n$ の $\alpha$ 番目の節点を $(n\alpha)$ などと表した節点はグローバルな節点番号を持っています。この対応が次のようになっているとします。
\begin{equation}
\begin{split}
&ローカルな番号 \hspace{20mm} 節点番号 \\
&\hspace{10mm} (n\alpha) \hspace{10mm} \Longleftrightarrow \hspace{10mm} I \\
&\hspace{10mm} (n\beta) \hspace{10mm} \Longleftrightarrow \hspace{10mm} J
\end{split} \notag
\end{equation}
この場合要素番号 $n$ の要素行列と要素ベクトルは、全体の係数行列 $K_{IJ}$、ベクトルと次のように対応します。
\begin{equation}
\begin{split}
&\hspace{5mm} 要素行列 \hspace{25mm} 係数行列 \\
&\hspace{10mm} K_{\alpha\beta}^{(n)} \hspace{10mm} \Longleftrightarrow \hspace{10mm} K_{IJ} \\
&\hspace{10mm} F_\alpha^{(n)} \hspace{10mm} \Longleftrightarrow \hspace{10mm} F_I
\end{split} \notag
\end{equation}
三角形要素のときの例としてあげた分割でも一つの節点が複数個の要素に共有されていることがあります。この場合上の対応は一対一ではなく多対一となり、係数行列の一つの行列要素 $K_{IJ}$ に対して複数個の要素行列が対応します。ですから係数行列の行列要素は対応する要素行列の行列要素の和となります。
\begin{equation}
K_{IJ}=K_{\alpha\beta}^{(n)}+K_{\gamma\delta}^{(m)}+\cdots \tag*{$(1.3-47)$}
\end{equation}
ここで、$I$ に対して $(n\alpha)$、$(m\gamma)$ などが対応し、$J$ に対して $(n\beta)$、$(m\delta)$ などが対応しています。
先の三角形要素の例を示したときはこのような要素行列から全体行列の作成を実際に行いましたが、要素数が多くなると大変な作業となります。
このような作業はコンピュータプログラムにかけばずっと効率的に行うことが出来ます。
手順をまとめると次のようになります。
まず、要素の積分点 $(r_i,s_i)$ ごとの補間関数とその微分を求めます。
\begin{equation}
\begin{split}
&N_\alpha(r_i,s_i) \\
&\frac{\partial}{\partial r}N_\alpha(r_i,s_i) \hspace{5mm} \frac{\partial}{\partial s}N_\alpha(r_i,s_i)
\end{split} \notag
\end{equation}
これより、
\begin{equation}
x=\sum_\alpha N_\alpha(r_i,s_i)x^\alpha \hspace{5mm} y=\sum_\alpha N_\alpha(r_i,s_i)y^\alpha \notag
\end{equation}
を使い変換行列、
\begin{equation}
\begin{bmatrix}
{\partial x}/{\partial r} & {\partial x}/{\partial s} \\
{\partial y}/{\partial r} & {\partial y}/{\partial s}
\end{bmatrix} \notag
\end{equation}
を求めます。これより(1.3-36)式のヤコビアン、
\begin{equation}
\frac{\partial(x,y)}{\partial(r,s)}=det
\begin{bmatrix}
{\partial x}/{\partial r} & {\partial x}/{\partial s} \\
{\partial y}/{\partial r} & {\partial y}/{\partial s}
\end{bmatrix} \notag
\end{equation}
と、次の逆行列を求めます。
\begin{equation}
\begin{bmatrix}
{\partial r}/{\partial x} & {\partial r}/{\partial y} \\
{\partial s}/{\partial x} & {\partial s}/{\partial y}
\end{bmatrix} \notag
\end{equation}
次にこれを使って補間関数の勾配を(1.3-30)式にしたがって計算します。
\begin{equation}
\begin{split}
&\frac{\partial}{\partial x}N_\alpha(r_i,s_i)=\frac{\partial}{\partial r}N_\alpha(r_i,s_i)\frac{\partial r}{\partial x}
+\frac{\partial}{\partial s}N_\alpha(r_i,s_i)\frac{\partial s}{\partial x} \\
&\frac{\partial}{\partial y}N_\alpha(r_i,s_i)=\frac{\partial}{\partial r}N_\alpha(r_i,s_i)\frac{\partial r}{\partial y}
+\frac{\partial}{\partial s}N_\alpha(r_i,s_i)\frac{\partial s}{\partial y}
\end{split} \notag
\end{equation}
これより要素行列の積分内の値、
\begin{equation}
\frac{\partial}{\partial x}N_\alpha(r_i,s_i)\epsilon\frac{\partial}{\partial x}N_\beta(r_i,s_i)
+\frac{\partial}{\partial y}N_\alpha(r_i,s_i)\epsilon\frac{\partial}{\partial y}N_\beta(r_i,s_i) \notag
\end{equation}
を計算し $k_{\alpha\beta}$ とします。
これに先ほど求めたヤコビアンと数値積分のための重み $w_i$ をかけます。
\begin{equation}
k_{\alpha\beta}\frac{\partial(x,y)}{\partial(r,s)}w_i \notag
\end{equation}
この値をすべての積分点で足しこみます。これでこの要素における要素行列 $K_{\alpha\beta}^{(n)}$ が求まりました。
最後に $(n\alpha)$、$(n\beta)$ に対応する節点番号 $I$、$J$ の係数行列の行列要素にここで求まった要素行列の値を足しこみます。
要素ベクトルも同様の方法で全体ベクトルの対応する成分に足しこみます。
以上で全体の係数行列とベクトルが求まりましたので、次にこの連立方程式が境界条件をみたすように修正してやる必要があります。
前にも言いましたように、ポテンシャルの法線方向の勾配つまり電場の法線成分がゼロの場合は自然境界条件となり何もしなくても自動的にこの条件が満たされます。またポテンシャルの値が決められているディレクレ境界では、対応する節点番号の行と列を縮小します。
特にポテンシャルの値がゼロの場合は、対応する行と列を除くだけで境界条件が満たされます。
ここで3角形要素のときと同じ例を使ってこの手順で計算を行ってみます。問題の図を下に再掲します。

この領域を下の図のように9個の四角形要素に分割します。節点数は三角形要素のときと同じく16になります。

計算結果を以下に示します。
\begin{equation}
\begin{split}
&\phi_{13}=0 \hspace{5mm} \phi_{14}=4.81585 \hspace{6mm} \phi_{15}=7.35435 \hspace{5mm} \phi_{16}=8.13784 \\
&\phi_{09}=0 \hspace{5mm} \phi_{10}=4.41488 \hspace{6mm} \phi_{11}=6.67133 \hspace{5mm} \phi_{12}=7.35435 \\
&\phi_{05}=0 \hspace{5mm} \phi_{06}=3.06264 \hspace{6mm} \phi_{07}=4.41488 \hspace{5mm} \phi_{08}=4.81585 \\
&\phi_{01}=0 \hspace{5mm} \phi_{02}=0 \hspace{22mm} \phi_{03}=0 \hspace{21mm} \phi_{04}=0
\end{split} \tag*{$(1.3-48)$}
\end{equation}
三角形要素の場合の結果(1.3-25)式との比較を下の図に示します。
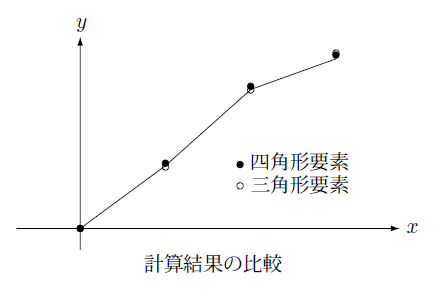
ここに実線で示したものはこの領域を $30\times 30=900$ 要素の四角形要素に分割した場合の値です。この結果を見ると、一辺3分割という粗い分割にもかかわらずより精度の高い解析の結果に近い値が得られていることが分かります。
