第4回 解析領域と対称性
有限要素法による磁場解析は有限の領域でモデル化します。
“有限”のモデルの境界には境界条件が必要になります。
境界は今見たいところ(評価点)が、境界条件によって、影響を受けないところに設定しなくてはなりません。
あまり、狭すぎると結果に影響があり、広すぎるとモデル規模が大きくなり計算時間が長くなる傾向になります。
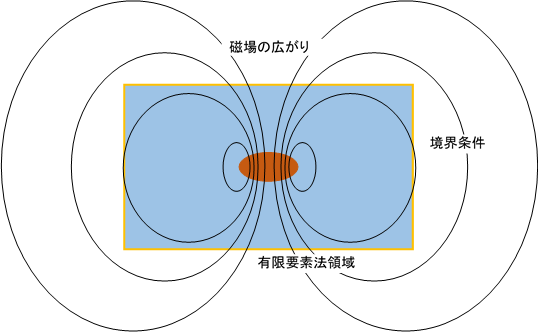
図4−1.磁場の広がりと有限要素法の解析領域
すべての解析対象について3次元解析を実施するのは得策とは言えません。
そこで、対称性を利用して、モデルを簡略化することを考え、効率的に解析を進めることが肝要です。
まず、考えたいのは、
2次元解析
軸対称解析
3次元解析
にするかどうかです。
計算時間は「3次元解析 > 2次元、軸対称」の傾向になります。
3次元解析は文字通り、解析対象をそのまま3次元でモデル化します。
2次元解析は無限に長い物の断面を取り出して、モデル化します。
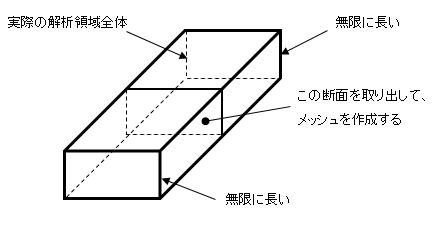
図4−2.2次元解析
とは言っても、実物は有限の長さなので、3次元的な影響がないか判断が必要です。
この判断ができれば、かなりの効率化が期待できます。
モーターの場合、長手方向(軸方向)はそれほど長くないですが、2次元解析でも、良い結果が得られます。
軸対称は円筒の解析領域の断面を取り出します。回転対称でなければなりません。
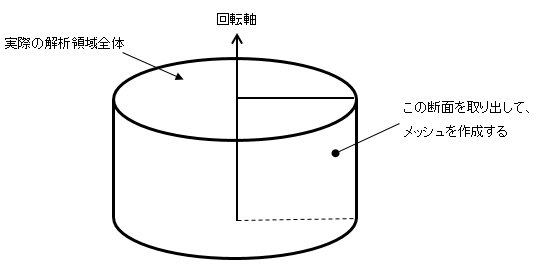
図4−3.軸対称解析
軸対称の磁場解析の場合、注意しなくてはならないのは、軸対称形状であっても、軸対称解析に適用できないケースがあります。
図4−4の(a)、(b)は共に形状が軸対称ですが、電流の向きが異なります。
図4−4(a)の電流の向きは軸方向、図4−4(b)の電流の向きは周方向です。軸対称解析で使用できる電流は周方向に限られます。
また、軸方向に流れる場合は3次元解析になります。
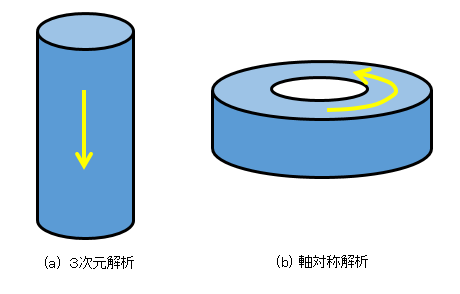
図4−4.軸対称解析に適さない場合
さらに、空間の対称性を利用すれば、さらに簡略化できます。
例として、四角い磁石と空気領域を考えます。ここでは、便宜的に2次元で考えます。
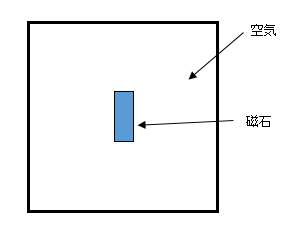
図4−5.概要図
対称性から4分の1モデルで十分となります。対称性を利用することで、新たな境界が出現しますが、適切な境界条件を設定すれば、問題ありません。
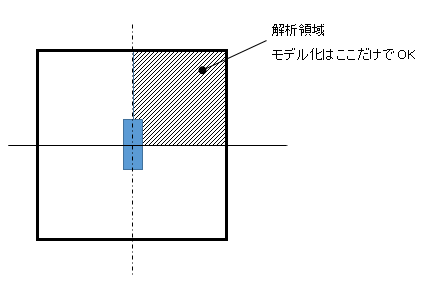
図4−6.4分の1モデル
上記の場合、解析規模は4分の1になり、その結果、計算時間も4分の1以下になります。
このように対称性を利用することで、かなりの効率化が期待できます。
●数値実験
この回の最初に有限要素法では有限の領域でモデル化を行うことを述べました。
コイルや磁性体などで構成された解析対象の周囲には空気領域を設けますが、空気領域の広さと解析結果がどの程度影響があるか数値実験によって、確認してみます。
解析の概要を下図に示します。形状は「第3回 メッシュ分割」の数値実験のモデルと同じですが、今回は静解析としました。
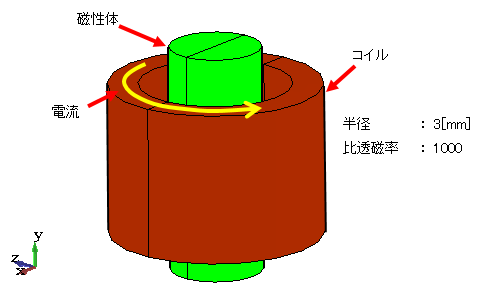
図4−7.数値実験用解析モデルの概要図
図4−8にメッシュ分割図を示します。境界位置が150mmの場合のものです。
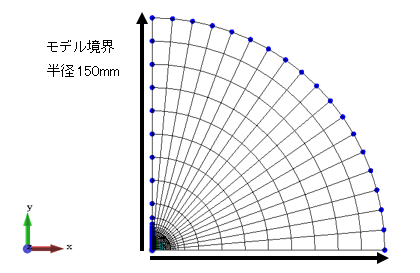
図4−8.メッシュ図(モデル境界150mm)
図4−9は中心付近の拡大図です。
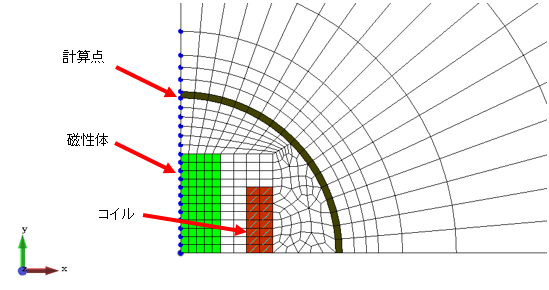
図4−9.メッシュ図の拡大図
計算点の要素中心は半径12mmとしています。
磁性体とコイルを囲むように計算点を配置しています。(5度おき)
図4−10に境界位置が150mmのときの磁束密度のベクトルを示します。
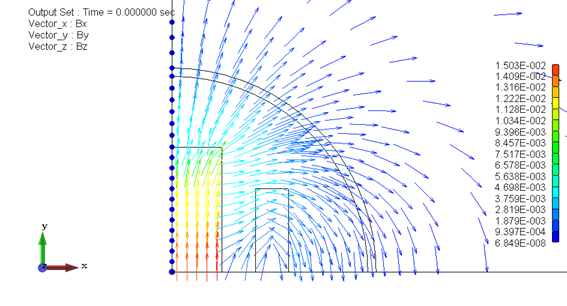
図4−10.磁束密度のベクトル図
同様にして、空気領域の広さを変更して、解析しました。計算点における磁束密度の径方向成分と空気領域の広さとの関係のグラフを図4−11に示します。
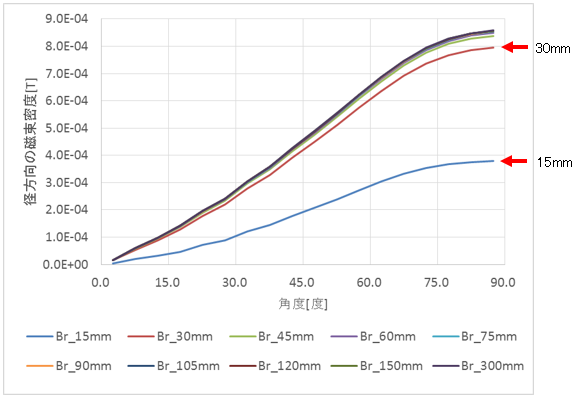
図4−11.空気領域の広さと磁束密度(径方向成分)
境界が60mm以降ではグラフが重なり、見づらいため、87.5度の要素(図4−12)に着目したグラフを図4−13に示します。
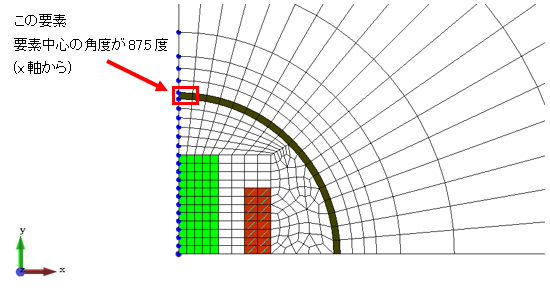
図4−12.着目する要素
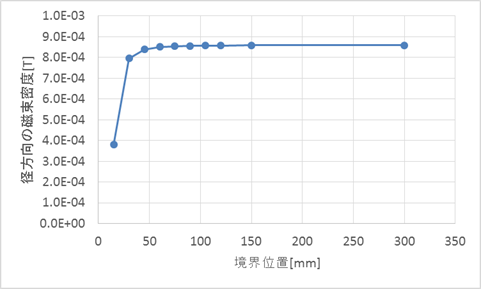
図4−13.87.5度の計算要素に着目した境界位置と磁束密度
下表は図4−13の数値データです。誤差は300mmを基準として、算出しています。
表4−1.数値データ
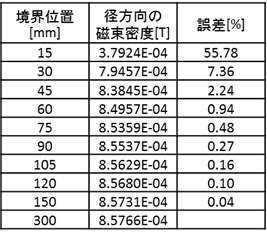
評価点の位置は12mmです。
このように空気領域が極端に狭いと影響を受けやすいことがわかります。
今回示しましたのは一例ですので、解析対象、評価点の位置や評価項目等によって、適切な空気領域が異なります。あまり狭くならないように注意が必要です。
●ポイント
対称性を利用すれば、効率良く解析ができる。
空気領域の広さが解析結果に影響を及ぼす。
ご意見・ご感想は
こちらから->
