一定の周波数 $f$ で振動する電磁場は一般の時間変化をする場合に比べて簡単に扱うことが出来ます。
角周波数、
\begin{equation}
\omega=2\pi f \tag*{$(4.2-1)$}
\end{equation}
をつかうとベクトルポテンシャル $\boldsymbol{A}$ の時間変化は三角関数で次のように表すことができます。
\begin{equation}
\boldsymbol{A}(\boldsymbol{x},t)=\boldsymbol{A}_1(\boldsymbol{x})\mathrm{sin}\omega t+\boldsymbol{A}_2(\boldsymbol{x})\mathrm{cos}\omega t \tag*{$(4.2-2)$}
\end{equation}
ここに $\boldsymbol{x}$ はベクトルポテンシャルの座標で $\boldsymbol{A}_1(\boldsymbol{x})$、$\boldsymbol{A}_2(\boldsymbol{x})$ は時間によらない位置だけに依存するベクトルです。
これより磁束密度は次のようにかけます。
\begin{equation}
\boldsymbol{B}(\boldsymbol{x},t)=\mathrm{rot}\boldsymbol{A}(\boldsymbol{x},t)=\mathrm{rot}\boldsymbol{A}_1(\boldsymbol{x})\mathrm{sin}\omega t+\mathrm{rot}\boldsymbol{A}_2(\boldsymbol{x})\mathrm{cos}\omega t \notag
\end{equation}
これより磁束密度も角周波数 $\omega$ で振動していることが分かります。
ところがベクトルポテンシャルの二乗を計算すると次のようになります。
\begin{equation}
(\boldsymbol{A}\cdot\boldsymbol{A})=|\boldsymbol{A}_1|^2\mathrm{sin}^2\omega t+2(\boldsymbol{A}_1\cdot\boldsymbol{A}_2)\mathrm{sin}\omega t\mathrm{cos}\omega t
+|\boldsymbol{A}_2|^2\mathrm{cos}^2\omega t \notag
\end{equation}
ここで、
\begin{equation}
\begin{split}
&\mathrm{sin}^2\omega t=\frac{1}{2}(1-\mathrm{cos}2\omega t) \hspace{10mm} \mathrm{cos}^2\omega t=\frac{1}{2}(1+\mathrm{cos}2\omega t) \\
&2\mathrm{sin}\omega t\mathrm{cos}\omega t=\mathrm{sin}2\omega t
\end{split} \notag
\end{equation}
なので2倍の角周波数の振動が現れ、もはや角周波数 $\omega$ の時間変化ではなくなってしまいます。したがって角周波数 $\omega$ で時間変化をする量はベクトルポテンシャルの一次式で表される必要があります。
それではベクトルポテンシャルを時間微分すればどうなるでしょうか。(4.2-2)式を時間微分すれば次のようになります。
\begin{equation}
\frac{\partial}{\partial t}\boldsymbol{A}(\boldsymbol{x},t)=\omega\boldsymbol{A}_1(\boldsymbol{x})\mathrm{cos}\omega t-\omega\boldsymbol{A}_2(\boldsymbol{x})\mathrm{sin}\omega t \notag
\end{equation}
これより時間微分しても角周波数が変化しないことが分かります。
ここで記号を簡略化するために次のオイラーの公式を使います。オイラーの公式は虚数単位を $j$ とかけば、
\begin{equation}
e^{j\theta}=\mathrm{cos}\theta+j\mathrm{sin}\theta \tag*{$(4.2-3)$}
\end{equation}
です。この微分をとると次のようになります。
\begin{equation}
\frac{d}{d\theta}e^{j\theta}=-\mathrm{sin}\theta+j\mathrm{cos}\theta=j(\mathrm{cos}\theta+j\mathrm{sin}\theta)=je^{j\theta} \notag
\end{equation}
このように虚数の指数関数は三角関数で表すことができ、微分をとっても指数関数の形は変わりません。
そこでベクトルポテンシャルを次のように表してみます。
\begin{equation}
\boldsymbol{A}(\boldsymbol{x},t)=\boldsymbol{A}_c(\boldsymbol{x})e^{j\omega t} \tag*{$(4.2-4)$}
\end{equation}
ここに $\boldsymbol{A}_c$ は複素数で実部と虚部に分けると次のようにかけます。
\begin{equation}
\boldsymbol{A}_c=\boldsymbol{A}_R+j\boldsymbol{A}_I \tag*{$(4.2-5)$}
\end{equation}
これよりベクトルポテンシャルは次のようになります。
\begin{equation}
\begin{split}
\boldsymbol{A}(\boldsymbol{x},t)&=(\boldsymbol{A}_R+j\boldsymbol{A}_I)(\mathrm{cos}\omega t+j\mathrm{sin}\omega t) \\
&=(\boldsymbol{A}_R\mathrm{cos}\omega t-\boldsymbol{A}_I\mathrm{sin}\omega t)+j(\boldsymbol{A}_R\mathrm{sin}\omega t+\boldsymbol{A}_I\mathrm{cos}\omega t)
\end{split} \tag*{$(4.2-6)$}
\end{equation}
ここではベクトルポテンシャルを複素数で表しましたが、実際は実数です。
この式の右辺の実部と虚部を見ればそれぞれ(4.2-2)式と同じく三角関数 $\mathrm{cos}\omega t$ と $\mathrm{sin}\omega t$ の和となっています。
したがって、複素数で表したベクトルポテンシャルの実部や虚部が実際のベクトルポテンシャルを表していると考えることが出来ます。
ただこのように表現しても、この複素数で表したベクトルポテンシャルを電磁場の方程式のような微分方程式に代入したときに、実部が虚部に影響したり、逆に虚部の影響が実部にあるようでは困ります。
結論から言いますと空間微分 $\mathrm{rot}$、$\mathrm{div}$ や時間微分のような線形演算の場合実部と虚部が混ざることはありません。
\begin{equation}
\begin{split}
&\mathrm{rot}\boldsymbol{A}=\mathrm{rot}(\boldsymbol{A}_R\mathrm{cos}\omega t-\boldsymbol{A}_I\mathrm{sin}\omega t)
+j\mathrm{rot}(\boldsymbol{A}_R\mathrm{sin}\omega t+\boldsymbol{A}_I\mathrm{cos}\omega t) \\
&\frac{\partial\boldsymbol{A}}{\partial t}=\frac{\partial}{\partial t}(\boldsymbol{A}_R\mathrm{cos}\omega t-\boldsymbol{A}_I\mathrm{sin}\omega t)
+j\frac{\partial}{\partial t}(\boldsymbol{A}_R\mathrm{sin}\omega t+\boldsymbol{A}_I\mathrm{cos}\omega t)
\end{split} \notag
\end{equation}
ここでもう少し具体的に説明するために、複素数から実部を取り出す記号を $\mathrm{Re}$、虚部を取り出す記号を $\mathrm{Im}$ として導入します。
\begin{equation}
\begin{split}
&\mathrm{Re}(\boldsymbol{A})=\boldsymbol{A}_R\mathrm{cos}\omega t-\boldsymbol{A}_I\mathrm{sin}\omega t \\
&\mathrm{Im}(\boldsymbol{A})=\boldsymbol{A}_R\mathrm{sin}\omega t+\boldsymbol{A}_I\mathrm{cos}\omega t
\end{split} \tag*{$(4.2-7)$}
\end{equation}
これらを時間微分すると、
\begin{equation}
\begin{split}
&\frac{\partial}{\partial t}\mathrm{Re}(\boldsymbol{A})=-\omega(\boldsymbol{A}_R\mathrm{sin}\omega t+\boldsymbol{A}_I\mathrm{cos}\omega t) \\
&\frac{\partial}{\partial t}\mathrm{Im}(\boldsymbol{A})=\omega(\boldsymbol{A}_R\mathrm{cos}\omega t-\boldsymbol{A}_I\mathrm{sin}\omega t)
\end{split} \tag*{$(4.2-8)$}
\end{equation}
となります。
一方、複素数で表現したベクトルポテンシャル(4.2-6)式を時間で微分すると次のようになります。
\begin{equation}
\frac{\partial}{\partial t}\boldsymbol{A}(\boldsymbol{x},t)
=-\omega(\boldsymbol{A}_R\mathrm{sin}\omega t+\boldsymbol{A}_I\mathrm{cos}\omega t)+j\omega(\boldsymbol{A}_R\mathrm{cos}\omega t-\boldsymbol{A}_I\mathrm{sin}\omega t)
=j\omega\boldsymbol{A}(\boldsymbol{x},t) \tag*{$(4.2-9)$}
\end{equation}
これと(4.2-6)式を比較すると次の関係が得られます。
\begin{equation}
\frac{\partial}{\partial t}\mathrm{Re}(\boldsymbol{A})+j\frac{\partial}{\partial t}\mathrm{Im}(\boldsymbol{A})
=\mathrm{Re}\bigl(\frac{\partial\boldsymbol{A}}{\partial t}\bigr)+\mathrm{Im}\bigl(\frac{\partial\boldsymbol{A}}{\partial t}\bigr) \tag*{$(4.2-10)$}
\end{equation}
これより時間微分と、実部虚部をとる操作 $\mathrm{Re}$、$\mathrm{Im}$ をどちらを先に行っても同じであることが分かります。
このように物理量を複素数で表すことをフェザー表示といいます。
さてこのようにベクトルポテンシャルを複素数で表すと方程式(4.1-8)式は次のようになります。
\begin{equation}
j\omega\sigma\boldsymbol{A}+\mathrm{rot}\boldsymbol{H}=\boldsymbol{J} \tag*{$(4.2-11)$}
\end{equation}
ここに磁場 $\boldsymbol{H}$ も電流密度 $\boldsymbol{J}$ も角周波数 $\omega$ で振動しています。
\begin{equation}
\begin{split}
&\boldsymbol{H}(\boldsymbol{x},t)=\boldsymbol{H}_c(\boldsymbol{x})e^{j\omega t} \\
&\boldsymbol{J}(\boldsymbol{x},t)=\boldsymbol{J}_c(\boldsymbol{x})e^{j\omega t}
\end{split} \notag
\end{equation}
このようになるには磁性体の透磁率が時間的に一定でなければなりません。
\begin{equation}
\boldsymbol{H}=\frac{1}{\mu}\boldsymbol{B}=\frac{1}{\mu}\mathrm{rot}\boldsymbol{A}=\frac{1}{\mu}\mathrm{rot}\boldsymbol{A}_ce^{j\omega t} \notag
\end{equation}
これより(4.2-11)式は次のようになります。
\begin{equation}
j\omega\sigma\boldsymbol{A}_ce^{j\omega t}+\mathrm{rot}\frac{1}{\mu}\mathrm{rot}\boldsymbol{A}_ce^{j\omega t}=\boldsymbol{J}_ce^{j\omega t} \notag
\end{equation}
時間依存項は共通なので省き $\boldsymbol{A}_c$ と $\boldsymbol{J}_c$ を改めて $\boldsymbol{A}$、$\boldsymbol{J}$ とかくと次の式が得られます。
\begin{equation}
j\omega\sigma\boldsymbol{A}+\mathrm{rot}\frac{1}{\mu}\mathrm{rot}\boldsymbol{A}=\boldsymbol{J} \tag*{$(4.2-12)$}
\end{equation}
これが周波数応答による磁場解析の基礎となる方程式です。
この方程式は時間依存を含む項が省かれているので右辺第1項を除いては、線形の静磁場の基礎方程式(2.1-5)式と同じ形をしています。
ただし、変数 $\boldsymbol{A}$、$\boldsymbol{J}$ は複素数として扱う必要があります。
ここで静磁場解析と同様に任意のベクトル関数 $\boldsymbol{w}$ と両辺の内積をとり、解析しようとしている領域すなわち解析領域 $V$ で体積積分すると次のようになります。
\begin{equation}
\int_V\boldsymbol{w}\cdot\bigl(j\omega\sigma\boldsymbol{A}+\mathrm{rot}\frac{1}{\mu}\mathrm{rot}\boldsymbol{A}\bigr)dV=\int_V\boldsymbol{w}\cdot\boldsymbol{J}dV \notag
\end{equation}
ここに $\boldsymbol{w}$ も複素数で、2次元問題の場合は $z$ 成分、軸対称問題の場合は円筒座標の $\theta$ 成分のみを持ちます。
左辺のカッコ内第2項は(2.4-4)式の上で変形したようにして次のように変形できます。
\begin{equation}
\int_V\mathrm{rot}\boldsymbol{w}\cdot\frac{1}{\mu}\mathrm{rot}\boldsymbol{A}dV-\int_S\boldsymbol{w}\cdot[\boldsymbol{H}\times\boldsymbol{n}]dS \notag
\end{equation}
したがって上の式は次のようになります。
\begin{equation}
j\omega\int_V\sigma\boldsymbol{w}\cdot\boldsymbol{A}dV+\int_V\mathrm{rot}\boldsymbol{w}\cdot\frac{1}{\mu}\mathrm{rot}\boldsymbol{A}dV=\int_V\boldsymbol{w}\cdot\boldsymbol{J}dV
+\int_S\boldsymbol{w}\cdot[\boldsymbol{H}\times\boldsymbol{n}]dS \tag*{$(4.2-13)$}
\end{equation}
空間の離散化を行うために有限要素法では解析領域を要素分割し上の積分を要素ごとの積分の和として表わし、要素内部でベクトルポテンシャルやベクトル関数を次のように補間します。
まず2次元や軸対称問題では節点要素を使うので $\alpha$ を要素内の節点番号として、
\begin{equation}
\begin{split}
&\boldsymbol{A}(\boldsymbol{x})=\sum_\alpha N_\alpha(\boldsymbol{x})\boldsymbol{A}^\alpha \\
&\boldsymbol{w}(\boldsymbol{x})=\sum_\alpha N_\alpha(\boldsymbol{x})\boldsymbol{w}^\alpha
\end{split} \tag*{$(4.2-14)$}
\end{equation}
と補間します。ここでベクトルポテンシャルやベクトル関数は複素数ですが、補間関数は三角形要素の場合は(1.3-15)式、四角形要素の場合は(1.3-28)式と同じになります。
3次元の場合は $\alpha$ を要素内の辺番号として、(2.6-1)式と同様に次のように補間されます。
\begin{equation}
\begin{split}
&\boldsymbol{A}(\boldsymbol{x})=\sum_\alpha\boldsymbol{N}_\alpha(\boldsymbol{x})A^\alpha \\
&\boldsymbol{w}(\boldsymbol{x})=\sum_\alpha\boldsymbol{N}_\alpha(\boldsymbol{x})w^\alpha
\end{split} \tag*{$(4.2-15)$}
\end{equation}
これらを使うと要素行列と要素ベクトル $K_{\alpha\beta}$ と$ F_\alpha$ は2次元問題では(2.2-6)式、軸対称問題では(2.3-8)式で表され、3次元問題では(2.6-2)式となります。
これに加えて(4.2-13)式の左辺第1項に対応して次の要素行列を定義します。
2次元や軸対称問題の場合、すなわち節点要素の場合は要素番号が $n$ の要素に対して、
\begin{equation}
C_{\alpha\beta}^{(n)}=\int_{V_n}N_\alpha\sigma N_\beta dV \tag*{$(4.2-16)$}
\end{equation}
とします。
また3次元の場合は、辺要素なので要素番号が $n$ の要素に対して次のようになります。
\begin{equation}
C_{\alpha\beta}^{(n)}=\int_{V_n}\boldsymbol{N}_\alpha\cdot\sigma\boldsymbol{N}_\beta dV \tag*{$(4.2-17)$}
\end{equation}
これらの要素行列と要素ベクトルを足しこんで作る全体行列と全体ベクトルを $C$、$K$、$F$ とかき未知数であるベクトルポテンシャルの全体ベクトルを $A$ とすれば、(4.2-13)式は離散化された次の行列方程式となります。
\begin{equation}
(j\omega C+K)A=F \tag*{$(4.2-18)$}
\end{equation}
要素行列(4.2-16)式や(4.2-17)式を見ると対称行列であることが分かりますので全体行列 $C$ も対称行列になります。
前に示したように $K$ は対称行列なのでこれよりこの連立方程式の係数行列は対称となります。
この連立方程式は複素数を係数とする方程式なので解いた結果得られるベクトルポテンシャルの節点値や辺の値は複素数になります。
したがってこれをもとに(4.2-14)式や(4.2-15)式を使って求めた要素内のベクトルポテンシャルも複素数となります。
ただしここで求まったものは時間依存を除いたものなのでこれに時間因子をかけたものがベクトルポテンシャルとなります。
この因子をかけたベクトルポテンシャルの実部をとると、(4.2-6)式より、
\begin{equation}
\boldsymbol{A}(\boldsymbol{x},t)=\mathrm{Re}\bigl(\boldsymbol{A}(\boldsymbol{x})e^{j\omega t}\bigr)
=\boldsymbol{A}_R(\boldsymbol{x})\mathrm{cos}\omega t-\boldsymbol{A}_I(\boldsymbol{x})\mathrm{sin}\omega t \tag*{$(4.2-19)$}
\end{equation}
となります。これより磁束密度は次のようになります。
\begin{equation}
\boldsymbol{B}=\boldsymbol{B}_R(\boldsymbol{x})\mathrm{cos}\omega t-\boldsymbol{B}_I(\boldsymbol{x})\mathrm{sin}\omega t \tag*{$(4.2-20)$}
\end{equation}
ここに、
\begin{equation}
\begin{split}
&\boldsymbol{B}_R=\mathrm{rot}\boldsymbol{A}_R \\
&\boldsymbol{B}_I=\mathrm{rot}\boldsymbol{A}_I
\end{split} \tag*{$(4.2-21)$}
\end{equation}
です。また電場は、
\begin{equation}
\boldsymbol{E}(\boldsymbol{x},t)=-\frac{\partial}{\partial t}\boldsymbol{A}(\boldsymbol{x},t)
=\omega\bigl(\boldsymbol{A}_R(\boldsymbol{x})\mathrm{sin}\omega t+\boldsymbol{A}_I(\boldsymbol{x})\mathrm{cos}\omega t\bigr) \tag*{$(4.2-22)$}
\end{equation}
となります。オームの法則よりこれに電気伝導率 $\sigma$ をかけると電流密度となります。
\begin{equation}
\boldsymbol{J}(\boldsymbol{x},t)=\sigma\omega\bigl(\boldsymbol{A}_R(\boldsymbol{x})\mathrm{sin}\omega t+\boldsymbol{A}_I(\boldsymbol{x})\mathrm{cos}\omega t\bigr) \tag*{$(4.2-23)$}
\end{equation}
これより導体内部での単位体積当たりのジュール損は周期 $T=1/f$ で平均して単位時間当たり次のようになります。
\begin{equation}
\begin{split}
W&=\frac{1}{T}\int_0^T\boldsymbol{J}\cdot\boldsymbol{E}dt \\
&=\frac{1}{T}\int_0^T\sigma\omega^2\bigl(\boldsymbol{A}_R(\boldsymbol{x})\mathrm{sin}\omega t+\boldsymbol{A}_I(\boldsymbol{x})\mathrm{cos}\omega t\bigr)^2dt \\
&=\sigma\omega^2\bigl\{|\boldsymbol{A}_R|^2\frac{1}{T}\int_0^T\mathrm{sin}^2\omega tdt
+(\boldsymbol{A}_R\cdot\boldsymbol{A}_I)\frac{1}{T}\int_0^T\mathrm{sin}2\omega tdt
+|\boldsymbol{A}_I|^2\frac{1}{T}\int_0^T\mathrm{cos}^2\omega tdt\bigr\} \\
&=\frac{1}{2}\sigma\omega^2(|\boldsymbol{A}_R|^2+|\boldsymbol{A}_I|^2)
\end{split} \tag*{$(4.2-24)$}
\end{equation}
前に言いましたようにこのような電場の二乗を含んだ計算をする場合は複素表現を使って計算することはできません。
ちなみに、
\begin{equation}
\boldsymbol{J}(\boldsymbol{x})\cdot\boldsymbol{E}(\boldsymbol{x})=\{-\sigma\omega(\boldsymbol{A}_R+j\boldsymbol{A}_I)\}\{-\omega(\boldsymbol{A}_R+j\boldsymbol{A}_I)\}
=\sigma\omega^2\bigl\{|\boldsymbol{A}_R|^2-|\boldsymbol{A}_I|^2+2j(\boldsymbol{A}_R\cdot\boldsymbol{A}_I)\bigr\} \notag
\end{equation}
となりこの実部をとっても(4.2-24)式と一致しません。このように時間変化がベクトルポテンシャルの線形和として表わすことが出来ないときは(4.2-19)式のように時間を含んだ表現で計算する必要があります。
これまで述べてきましたが周波数応答による解析では非線形の磁性体を扱うことが出来ません。ただし強磁性体を扱う場合透磁率が線形であるのは、かなり磁場が小さな時であり一般には非線形領域になる場合が多くあります。
磁性体が非線形になると磁場が一定の周波数で振動しても磁束密度は一定の周波数とはならずひずんだ波形となります。また磁場がゼロのときの初期透磁率のままですと、磁場が大きくなるにつれて実際の磁束密度より大きな磁束密度となってしまいます。
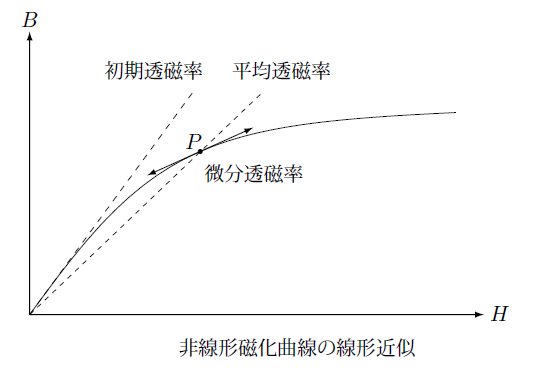
磁場が大きくなり上の図の点 $P$ になると初期透磁率を使った場合より磁束密度はかなり小さくなります。
バイアス磁場がありこの点を中心に小さく振動しているような場合は、磁化曲線の接線上を点 $P$ を中心に振動しているとして近似できます。
したがって透磁率は初期透磁率を使うのではなく微分透磁率、
\begin{equation}
\mu_d=\frac{dB}{dH} \tag*{$(4.2-25)$}
\end{equation}
を使うことでより実際の現象に近い線形解析ができます。
原点を中心に点 $P$ を最大磁場となるような振動の場合は、その点における磁場と磁束密度から計算される平均透磁率、
\begin{equation}
\mu_a=\frac{B}{H} \tag*{$(4.2-26)$}
\end{equation}
を使ったほうが初期透磁率より磁束密度の最大値を再現できることが分かります。
このように周波数応答解析を行う場合、磁性体の非線形性をどのように考慮するかは現実的な解析を行う上で非常に重要なことです。
技術情報 Techinicalinfo
- ホーム
- 技術情報
- 【技術情報】有限要素法入門
- 4.2 周波数応答解析
【技術情報】有限要素法入門
