A1.積分公式
電磁場解析でよく使う積分公式をまとめておきます。
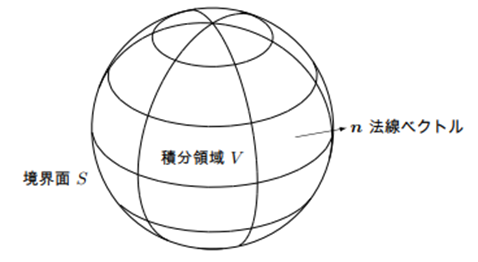
ガウスの発散定理
ベクトル場の発散の体積積分を表面積分で表すことができます。
\begin{equation}
\int_V\mathrm{div}\boldsymbol{v}dV=\int_S\boldsymbol{v}\cdot\boldsymbol{n}dS \tag*{$(A1-1)$}
\end{equation}
ここに $V$ は体積領域、$S$ はその領域の境界面、$\boldsymbol{n}$ は境界面に外向きにとった単位法線ベクトルです。
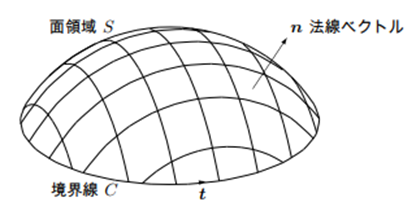
ストークスの定理
ベクトル場の回転の面積積分を境界積分で表すことができます。
\begin{equation}
\int_S\mathrm{rot}\boldsymbol{v}\cdot\boldsymbol{n}dV=\int_C\boldsymbol{v}\cdot\boldsymbol{t}dl \tag*{$(A1-2)$}
\end{equation}
ここに $S$ は面領域、$C$ はその領域の境界線、$\boldsymbol{n}$ は境界面に外向きにとった単位法線ベクトルです。
A2.ベクトルの成分計算
例えば(5-12)式、
\begin{equation}
\mathrm{rot}(\mathrm{rot})=\mathrm{grad}(\mathrm{div})-\Delta \notag
\end{equation}
などを確認する計算を行うときはベクトルを成分になおし丹念に計算する必要があります。このような計算を効率よく行うための方法を述べます。まず二つのベクトルの内積は次のように成分でかくことができます。
\begin{equation}
\boldsymbol{A}\cdot\boldsymbol{B}=A_xB_x+A_yB_y+A_zC_z=\sum_{i=1}^3A_iB_i \tag*{$(A2-1)$}
\end{equation}
この式の右辺のように一つの項に同じ添字が2度現れる場合はこの添字について1から3までの和をとる場合が多くあります。また和をとる添字がいくつもある場合など頻繁に和の記号をかく必要があります。そこでこのような場合、つまり一つの項に同じ添字が2度現れた場合はこの添え字に関して1から3までの和をとるものとして
和の記号を省略することにします。
\begin{equation}
\sum_{i=1}^3A_iB_i=A_iB_i \tag*{$(A2-2)$}
\end{equation}
この決まりのことをアインシュタインの規約といいます。これよりベクトルの内積は次のようにかけます。
\begin{equation}
\boldsymbol{A}\cdot\boldsymbol{B}=A_iB_i \tag*{$(A2-3)$}
\end{equation}
ここで計算に便利な二つの記号を導入します。一つはクロネッカのデルタとよばれるもので次のように定義されています。
\begin{equation}
\begin{split}
\delta_{ij}&=1 \hspace{15mm} (i=j) \\
&=0 \hspace{15mm} (i\ne j)
\end{split} \tag*{$(A2-4)$}
\end{equation}
この記号を使うと基底ベクトルの内積を次のように表すことができます。
\begin{equation}
\boldsymbol{e}_i\cdot\boldsymbol{e}_j=\delta_{ij} \notag
\end{equation}
もう一つの記号はレビ・チビタの記号とよばれるもので、
\begin{equation}
\begin{split}
e_{ijk}&=+1 \hspace{15mm} (i,j,k が 1,2,3の偶置換の場合) \\
&=-1 \hspace{15mm} (i,j,k が 1,2,3の奇置換の場合) \\
&= \hspace{3mm}0 \hspace{15mm} (それ以外の場合)
\end{split} \tag*{$(A2-5)$}
\end{equation}
例えば、
\begin{equation}
\begin{split}
&e_{123}=e_{231}=e_{312}=1 \\
&e_{321}=e_{213}=e_{132}=-1 \\
&e_{111}=e_{112}=e_{122}=0
\end{split} \notag
\end{equation}
などです。これを使うとベクトルどうしの外積は次のようにかくことができます。
\begin{equation}
[\boldsymbol{A}\times\boldsymbol{B}]_i=e_{ijk}A_jB_k \tag*{$(A2-6)$}
\end{equation}
このようになることは実際に計算して確かめることができます。
\begin{equation}
[\boldsymbol{A}\times\boldsymbol{B}]_1=e_{1jk}A_jB_k=e_{123}A_2B_3+e_{132}A_3B_2=A_2B_3-A_3B_2 \notag
\end{equation}
他の成分も同じように確かめることができます。
これより、勾配、発散、回転などは次のように表すことができます。
まず勾配は、
\begin{equation}
(\mathrm{grad}f)_i=\frac{\partial f}{\partial x_i} \tag*{$(A2-7)$}
\end{equation}
発散は、
\begin{equation}
\mathrm{div}\boldsymbol{V}=\frac{\partial V_i}{\partial x_i} \tag*{$(A2-8)$}
\end{equation}
回転は、
\begin{equation}
(\mathrm{rot}\boldsymbol{V})_i=e_{ijk}\frac{\partial V_k}{\partial x_j} \tag*{$(A2-9)$}
\end{equation}
とかけます。これを使って二つのベクトルの外積の発散を計算してみます。
\begin{equation}
\begin{split}
\mathrm{div}[\boldsymbol{A}\times\boldsymbol{B}]&=\frac{\partial}{\partial x_i}(e_{ijk}A_jB_k) \\
&=e_{ijk}\frac{\partial A_j}{\partial x_i}B_k+e_{ijk}A_j\frac{\partial B_k}{\partial x_i} \\
&=\mathrm{rot}\boldsymbol{A}\cdot\boldsymbol{B}-\boldsymbol{A}\cdot\mathrm{rot}\boldsymbol{B}
\end{split} \notag
\end{equation}
このようにベクトルの成分ごとに式をかき出さなくてもこのような計算ができてしまいます。さらに便利な公式があります。レビ・チビタの縮約公式とよばれているもので次のものです。
\begin{equation}
e_{ijk}e_{ilm}=\delta_{jl}\delta_{km}-\delta_{jm}\delta_{kl} \tag*{$(A2-10)$}
\end{equation}
左辺はレビ・チビタの記号どうしの積ですが同じ添字 $i$ が2度現れていますのでこれについて1から3までの和をとっています。この関係を示すにはそれぞれの添字の組み合わせについてひとつづつ確かめる必要がありますので少し面倒です。しかしこの公式を使うと複雑な成分計算を簡単に行えるので非常に重宝します。
縮約公式を使った例として次の外積に関する式を確認します。
\begin{equation}
[\boldsymbol{A}\times[\boldsymbol{B}\times\boldsymbol{C}]]=(\boldsymbol{A}\cdot\boldsymbol{C})\boldsymbol{B}-(\boldsymbol{A}\cdot\boldsymbol{B})\boldsymbol{C} \notag
\end{equation}
左辺の $i$ 成分を計算すると次のようになります。
\begin{equation}
\begin{split}
[\boldsymbol{A}\times[\boldsymbol{B}\times\boldsymbol{C}]]_i&=e_{ijk}A_j(e_{klm}B_lC_m) \\
&=e_{ijk}e_{klm}A_jB_lC_m \\
&=(\delta_{il}\delta_{jm}-\delta_{im}\delta_{jl})A_jB_lC_m \\
&=A_jB_iC_j-A_jB_jC_i \\
&=\bigl((\boldsymbol{A}\cdot\boldsymbol{C})\boldsymbol{B}-(\boldsymbol{A}\cdot\boldsymbol{B})\boldsymbol{C}\bigr)_i
\end{split} \notag
\end{equation}
このように簡単に求まりますが成分ごとに計算すると結構大変です。
最後に、前に例として出した回転演算子を2回作用させた場合の計算をしておきます。
\begin{equation}
\begin{split}
\bigl(\mathrm{rot}(\mathrm{rot}\boldsymbol{V})\bigr)_i&=e_{ijk}\frac{\partial}{\partial x_j}\Bigl(e_{klm}\frac{\partial V_m}{\partial x_l}\Bigr) \\
&=e_{kij}e_{klm}\frac{\partial}{\partial x_j}\frac{\partial V_m}{\partial x_l} \\
&=(\delta_{il}\delta_{jm}-\delta_{im}\delta_{jl})\frac{\partial}{\partial x_j}\frac{\partial V_m}{\partial x_l} \\
&=\frac{\partial}{\partial x_j}\frac{\partial V_j}{\partial x_i}-\frac{\partial}{\partial x_j}\frac{\partial V_i}{\partial x_j} \\
&=\bigl(\mathrm{grad}(\mathrm{div}\boldsymbol{V})-\Delta\boldsymbol{V}\bigr)_i
\end{split} \notag
\end{equation}
技術情報 Techinicalinfo
【技術情報】ベクトル解析入門
