ここで、自由エネルギーによる磁性体の表現についてもう少し議論します。磁場解析はアンペールの法則をもとにしていますので電流が既知として磁束密度を求めます。
このことは磁場を決めて磁束密度を求めることと同等なので自由エネルギーの変数も磁束密度よりも磁場にした方が都合がよいことになります。
そこで次のような熱力学ポテンシャル $G$ を定義します。
\begin{equation}
G(T,\boldsymbol{H})=F(T,\boldsymbol{B})-\boldsymbol{H}\cdot\boldsymbol{B} \tag*{$(3.4-1)$}
\end{equation}
この微分は(3.3-17)式より次のようになります。
\begin{equation}
dG(T,\boldsymbol{H})=-SdT-\boldsymbol{B}\cdot d\boldsymbol{H} \tag*{$(3.4-2)$}
\end{equation}
これより次の関係が得られます。\begin{equation}
S=-\frac{\partial G}{\partial T} \hspace{10mm} B_i=-\frac{\partial G}{\partial H_i} \tag*{$(3.4-3)$}
\end{equation}
熱力学によりますと温度と磁場が定まっている場合この熱力学ポテンシャルが最小になります。
これは考えている領域 $V$ において積分、
\begin{equation}
I=\int_VG(T,\boldsymbol{H})dV \tag*{$(3.4-4)$}
\end{equation}
が最小になることです。熱力学ポテンシャル $G$ は温度と磁場の関数なのでこの積分 $I$ もこれらの関数です。
しかし今これらを固定したうえで最小値を求めるのですからどう考えればよいのでしょうか。
実は磁性体の状態変数は温度と磁場だけでなく磁化や磁束密度もあります。
熱平衡状態では温度と磁場が決まればこれらの状態変数が決まるのでこの二つの変数の関数としてかけるのですが、
熱平衡状態を求めようとしているのですから磁化や磁束密度も自由に動かすことができるのです。
したがって、この積分 $I$ を最小にすることによって熱平衡状態を求め磁化特性が決まります。
ここでは、この積分が最小値になるように磁束密度を求めることを考えます。
この場合 $I$ を磁束密度 $\boldsymbol{B}$ の関数としてこの最小値を求めます。
一般に関数の最小値を求める場合変数を動かしても関数が変化しない極値を求めるという方法がとられます。
この場合積分の変化 $\delta I$ は磁束密度の無限小の変化 $\delta\boldsymbol{B}$ に対して次のようになります。
\begin{equation}
\delta I(\boldsymbol{B})=I(\boldsymbol{B}+\delta\boldsymbol{B})-I(\boldsymbol{B})=\frac{\partial I}{\partial\boldsymbol{B}}\cdot\delta\boldsymbol{B} \notag
\end{equation}
これを積分 $I$ の磁束密度 $\boldsymbol{B}$ による変分といいます。ここに、
\begin{equation}
\frac{\partial I}{\partial\boldsymbol{B}}\cdot\delta\boldsymbol{B}=\sum_i\frac{\partial I}{\partial B_i}\delta B_i \notag
\end{equation}
です。
極値ではこれがゼロとなるので、
\begin{equation}
\delta I(\boldsymbol{B})=0 \tag*{$(3.4-5)$}
\end{equation}
です。この式は(3.4-1)式より次のようにかけます。
\begin{equation}
\delta\int_V\bigl\{F(T,\boldsymbol{B})-\boldsymbol{H}\cdot\boldsymbol{B}\bigr\}dV=0 \tag*{$(3.4-6)$}
\end{equation}
左辺は、
\begin{equation}
\begin{split}
\int_V\bigl\{\frac{\partial}{\partial\boldsymbol{B}}F(T,\boldsymbol{B})\cdot\delta\boldsymbol{B}-\boldsymbol{H}\cdot\delta\boldsymbol{B}\bigr\}dV
=\int_V\delta\boldsymbol{B}\cdot\bigl\{\frac{\partial}{\partial\boldsymbol{B}}F(T,\boldsymbol{B})-\boldsymbol{H}\bigr\}dV
\end{split} \notag
\end{equation}
となりますが、変分をベクトルポテンシャル $\boldsymbol{A}$ であらわすと次のようになります。
\begin{equation}
\int_V\delta(\mathrm{rot}\boldsymbol{A})\cdot\bigl(\frac{\partial F}{\partial\boldsymbol{B}}-\boldsymbol{H}\bigr)dV
=\int_V\mathrm{rot}(\delta\boldsymbol{A})\cdot\bigl(\frac{\partial F}{\partial\boldsymbol{B}}-\boldsymbol{H}\bigr)dV \notag
\end{equation}
さらに部分積分によって変形すると次のようになります。
\begin{equation}
\int_V\delta\boldsymbol{A}\cdot\mathrm{rot}\bigl(\frac{\partial F}{\partial\boldsymbol{B}}-\boldsymbol{H}\bigr)dV
+\int_S\delta\boldsymbol{A}\cdot\bigl[\bigl(\frac{\partial F}{\partial\boldsymbol{B}}\bigr)\times\boldsymbol{n}\bigr]dS \notag
\end{equation}
第2項は体積領域 $V$ の表面 $S$ における表面積分で $\boldsymbol{n}$ はこの表面に外向きにとった単位法線ベクトルです。
境界面において変分をゼロにとればこの表面積分は消えるので、(3.4-6)式は次のようになります。
\begin{equation}
\int_V\delta\boldsymbol{A}\cdot\mathrm{rot}\bigl(\frac{\partial F}{\partial\boldsymbol{B}}-\boldsymbol{H}\bigr)dV=0 \tag*{$(3.4-7)$}
\end{equation}
ここで磁場は固定して変分をとったのですが、磁性体内部の磁場 $\boldsymbol{H}$ の分布はわかっていません。ところが、
\begin{equation}
\mathrm{rot}\boldsymbol{H}=\boldsymbol{J} \tag*{$(3.4-8)$}
\end{equation}
であり、電流密度は既知の量なので(3.4-7)式は、
\begin{equation}
\int_V\delta\boldsymbol{A}\cdot\bigl(\mathrm{rot}\frac{\partial F}{\partial\boldsymbol{B}}-\boldsymbol{J}\bigr)dV=0 \tag*{$(3.4-9)$}
\end{equation}
となります。これが熱力学ポテンシャル $G$ を温度と磁場を固定して磁束密度で変分をとりそれをゼロとすることによって得られた方程式です。
このように熱力学ポテンシャルなどの体積積分を最小にするために変分をとって極値を求めることを変分法とよび、今回のように変分をとることによって物理法則が得られることを変分原理といいます。
ここで少し補足説明をしておきます。この変分原理を導出するのにあたり(3.4-8)式を使っているので、変分原理だけでこの方程式は導出されたのではないというと思われるかもしれません。しかしここではこの式を電流密度から磁場を求める関係として使っている
わけではありません。磁場 $\boldsymbol{H}$ は制御変数なのでこれを固定して考えているので磁場を求めるために使っているのではなく、この式を使って制御変数を電流密度にかきかえているということです。
今まで磁場解析の基礎方程式であるアンペールの法則に対して任意のベクトル関数 $\boldsymbol{w}$ をかけて積分することによって有限要素法の基礎方程式を求めてきました。
\begin{equation}
\int_V\boldsymbol{w}\cdot\bigl(\mathrm{rot}\boldsymbol{H}-\boldsymbol{J}\bigr)dV=0 \tag*{$(3.4-10)$}
\end{equation}
この式と今回求まった(3.4-9)式を比較すると、ベクトルポテンシャルの変分 $\delta\boldsymbol{A}$ は任意にとれるので任意のベクトル関数 $\boldsymbol{w}$ と見做せます。したがて両者の違いは(3.4-10)式では磁場 $\boldsymbol{H}$ を磁束密度の関数として与えなけらばならないのに対して、今回変分法から導かれた(3.4-9)式では自由エネルギーの磁束密度依存性が分かればよいことになります。
両者を比較すると次のようになります。
\begin{equation}
\begin{split}
&\boldsymbol{H}=\boldsymbol{H}(\boldsymbol{B}) \\
&F=F(\boldsymbol{B})
\end{split} \notag
\end{equation}
ただし温度依存性はこの議論では省いています。この式を比較すると前者はベクトルどうしの関係なので非常に自由度があり、物理的に許されない関係も含まれてしまいます。一方後者は自由エネルギーというスカラー関数の関係であり、磁束密度の成分の二乗に依存することが分かっているので測定によって決定することは十分可能です。
さらに決定的な違いは、一般の強磁性体の磁化特性は磁化過程の履歴に依存するヒステリシスを持っています。磁場を磁束密度の関数と考えると磁束密度が決まれば磁場が決まってしまいこのヒステリシスを表現することはできません。一方自由エネルギーを使う場合この磁束密度と磁場の関係が、
\begin{equation}
\boldsymbol{H}=\frac{\partial F}{\partial\boldsymbol{B}} \tag*{$(3.4-11)$}
\end{equation}
なので磁束密度が決まっても異なった磁場となることが可能です。
この様子を一次元の場合について示します。磁束密度の成分は一つしかないのでそれを $B$ とかけば自由エネルギーはこれの二乗の関数として表現されます。
これを $B^2$ の2次まで展開し定数項を無視すると次のようになります。
\begin{equation}
F(B^2)=C_1B^2+C_2B^4 \tag*{$(3.4-12)$}
\end{equation}
これより、
\begin{equation}
H=\frac{\partial F}{\partial B}=2C_1B+4C_2B^3 \notag
\end{equation}
これより磁場 $H$ が決まると上の関係をみたす磁束密度$B$が求まりますが一つになるとは限りません。
例えば磁場がゼロになる場合、
\begin{equation}
2C_1B+4C_2B^3=0 \notag
\end{equation}
となりますがこの方程式の解は次のようになります。
\begin{equation}
B=0 \hspace{2mm} , \hspace{2mm} \pm\sqrt{\frac{-C_1}{2C_2}} \notag
\end{equation}
したがって(3.4-12)式の係数 $C_1$、$C_2$ がどちらも正の場合は磁束密度がゼロのときに限って磁場がゼロになりますが、
係数 $C_1$ が負の場合は磁束密度がゼロでない二つの場合にも磁場がゼロとなります。
この様子を下の図に示しました。
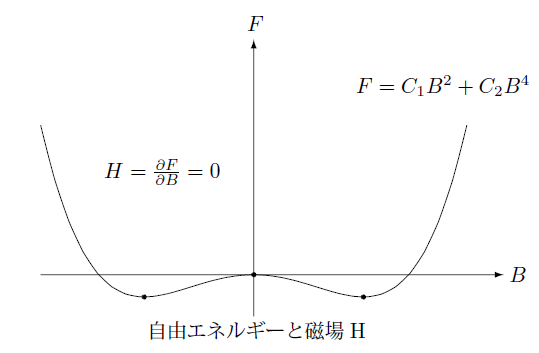
このとき $B=0$ は自由エネルギーが極大となるため不安定となり、磁束密度はゼロでない値を持ちます。
すなわち磁場がゼロでも磁束密度がゼロでない状態が実現します。このときは磁化もゼロなりません。
このような状態を自発磁化とよんでおりヒステリシスの一つの原因となています。
ここでは自由エネルギーを導入し、温度や、磁束密度という状態変数によって表される状態量であることを述べました。
熱力学によるとこの自由エネルギーはこの状態変数つまり温度と磁束密度を固定した場合、熱平衡状態では最小値をとります。
通常の磁性体は一定の電磁場の中に一定の温度でしばらく置かれているとこの状態になっていると思われます。
アンペールの法則では電流をコントロールすれば磁場 $\boldsymbol{H}$ が決まることになるので、制御変数としては磁場を使った方が便利です。
そこで自由エネルギーの変数である磁束密度を磁場に変えた状態量として熱力学ポテンシャル $G$ を導入しました。
これは温度と磁場を一定にした場合最小値をとりますので、考えている領域の熱力学ポテンシャルの極値を求める変分法を導入しました。
その結果自由エネルギーを磁束密度の関数として与えてやれば一般的な異方性非線形の磁性体が扱えることを示しました。
またこの方法では磁場を磁束密度の関数として扱わないのでヒステリシスの表現が可能です。
