微分方程式を解くには境界条件が必要になります。静電場の方程式も微分方程式ですから解くためには境界条件を考慮しなければなりません。
境界条件には、第一種境界条件、第二種境界条件などがあります。
境界で電位つまりポテンシャルが決まっている場合が第一種境界条件で、ポテンシャルの勾配すなわち電場の法線成分が定まっている場合を
第二種境界条件といいます。
まず第一種境界条件から考えます。この境界条件はディレクレ境界条件ともよばれており境界上でポテンシャルの値が決まっています。
この境界条件を有限要素法に適用するためには境界上の節点のポテンシャル値を与えられた境界条件のポテンシャル値とする必要があります。
有限要素法ではポテンシャルの節点値を未知数とした連立方程式を解くので、この条件を適用するためには境界上の節点に対応する未知数を方程式から除くことになります。
例えば次の連立方程式を考えます。
\begin{equation}
\begin{bmatrix}
k_{1,1} & \cdots & k_{1,i-1} & k_{1,i} & k_{1,i+1} & \cdots & k_{1,n} \\
\vdots & \ddots & \vdots & \vdots & \vdots & \ddots & \vdots \\
k_{i-1,1} & \cdots & k_{i-1,i-1} & k_{i-1,i} & k_{i-1,i+1} & \cdots & k_{i-1,n} \\
k_{i,1} & \cdots & k_{i,i-1} &k_{i,i} & k_{i,i+1} & \cdots & k_{i,n} \\
k_{i+1,1} & \cdots & k_{i+1,i-1} & k_{i+1,i} & k_{i+1,i+1} & \cdots & k_{i+1,n} \\
\vdots & \ddots & \vdots & \vdots & \vdots & \ddots & \vdots \\
k_{n,1} & \cdots & k_{n,i-1} & k_{n,i} & k_{n,i+1} & \cdots & k_{n,n}
\end{bmatrix}
\begin{bmatrix}
\phi_1 \\
\vdots \\
\phi_{i-1} \\
\phi_i \\
\phi_{i+1} \\
\vdots \\
\phi_n
\end{bmatrix}
=
\begin{bmatrix}
f_1 \\
\vdots \\
f_{i-1} \\
f_i \\
f_{i+1} \\
\vdots \\
f_n
\end{bmatrix} \notag
\end{equation}
ここで境界条件として $i$ 番目のポテンシャル $\phi_i$ が定まっているとします。するとこれは未知ではなく既知なので上の連立方程式を変形してこれに関連する項を右辺に移項します。すると下の方程式となります。
\begin{equation}
\begin{bmatrix}
k_{1,1} & \cdots & k_{1,i-1} & k_{1,i+1} & \cdots & k_{1,n} \\
\vdots & \ddots & \vdots & \vdots & \ddots & \vdots \\
k_{i-1,1} & \cdots & k_{i-1,i-1} & k_{i-1,i+1} & \cdots & k_{i-1,n} \\
k_{i,1} & \cdots & k_{i,i-1} & k_{i,i+1} & \cdots & k_{i,n} \\
k_{i+1,1} & \cdots & k_{i+1,i-1} & k_{i+1,i+1} & \cdots & k_{i+1,n} \\
\vdots & \ddots & \vdots & \vdots & \ddots & \vdots \\
k_{n,1} & \cdots & k_{n,i-1} & k_{n,i+1} & \cdots & k_{n,n}
\end{bmatrix}
\begin{bmatrix}
\phi_1 \\
\vdots \\
\phi_{i-1} \\
\\
\phi_{i+1} \\
\vdots \\
\phi_n
\end{bmatrix}
=
\begin{bmatrix}
f_1 \\
\vdots \\
f_{i-1} \\
f_i \\
f_{i+1} \\
\vdots \\
f_n
\end{bmatrix}
–
\begin{bmatrix}
k_{1,i}\phi_i \\
\vdots \\
k_{i-1,i}\phi_i \\
k_{i,i}\phi_i \\
k_{i+1,i}\phi_i \\
\vdots \\
k_{n,i}\phi_i
\end{bmatrix} \notag
\end{equation}
このように変形すると未知数の数は $n$ から $n-1$ となりますが方程式の数は $n$ のままであり、方程式の数が多くなってしまいます。
そこでこの方程式の $i$ 行目の方程式を取り除きます。
\begin{equation}
\begin{bmatrix}
k_{1,1} & \cdots & k_{1,i-1} & k_{1,i+1} & \cdots & k_{1,n} \\
\vdots & \ddots & \vdots & \vdots & \ddots & \vdots \\
k_{i-1,1} & \cdots & k_{i-1,i-1} & k_{i-1,i+1} & \cdots & k_{i-1,n} \\
k_{i+1,1} & \cdots & k_{i+1,i-1} & k_{i+1,i+1} & \cdots & k_{i+1,n} \\
\vdots & \ddots & \vdots & \vdots & \ddots & \vdots \\
k_{n,1} & \cdots & k_{n,i-1} & k_{n,i+1} & \cdots & k_{n,n}
\end{bmatrix}
\begin{bmatrix}
\phi_1 \\
\vdots \\
\phi_{i-1} \\
\phi_{i+1} \\
\vdots \\
\phi_n
\end{bmatrix}
=
\begin{bmatrix}
f_1 \\
\vdots \\
f_{i-1} \\
f_{i+1} \\
\vdots \\
f_n
\end{bmatrix}
–
\begin{bmatrix}
k_{1,i}\phi_i \\
\vdots \\
k_{i-1,i}\phi_i \\
k_{i+1,i}\phi_i \\
\vdots \\
k_{n,i}\phi_i
\end{bmatrix} \notag
\end{equation}
このようにして変形すると係数行列は $n-1$ 行 $n-1$ 列の行列となり最初の連立方程式より元数が一つ小さな方程式となります。
また、縮小後の係数行列も対称行列になることが分かります。
このようにしてこの境界条件の節点に対してこの操作を繰り返すと境界上の節点の数だけ縮小した係数行列を持つ方程式が得られます。
ポテンシャルの値が分かっているディレクレ境界条件はこのように有限要素法の係数行列を縮小して適用することができます。
次に第二種境界条件についてですが、静電場解析の場合この境界条件はポテンシャルの法線方向の勾配を指定する条件となります。
1.4節では、静電場の方程式(1.4-1)式を(1.4-3)式に変形するとき境界積分が出てきますが、この項は境界条件によって考慮されるので省略できるとして話を進めてきました。この境界積分は、
\begin{equation}
\int_V\sum_{i=1}^3\bigl(w\epsilon\frac{\partial\phi}{\partial x_i}\bigr)dV
=\int_Sw\epsilon(\boldsymbol{\nabla}\phi\cdot\boldsymbol{n})dS \notag
\end{equation}
ですが、ここで、
\begin{equation}
\boldsymbol{D}=-\epsilon\boldsymbol{\nabla}\phi \notag
\end{equation}
ですからポテンシャルの法線方向の勾配すなわち電束密度の法線成分がゼロの場合この積分はゼロとなり省略できたのです。
ところが一般的には電束密度の法線成分の値がゼロではなく決まった値を持つ境界条件を与える場合があります。
このような場合はこの積分は省略できず要素行列と要素ベクトルを作る段階で境界上の節点を持つ要素についてその補間関数から、
\begin{equation}
\int_{S_n}N_\alpha D_ndS \notag
\end{equation}
を計算して要素ベクトルに加える必要があります。ここに $D_n$ は指定された電束密度の値であり、面積分は境界面を含む要素番号 $n$ の境界面 $S_n$ で行います。
境界面での電束密度の法線成分が指定される境界条件とはどのようなものかといいますと、例えば金属の表面では表面電荷密度に対応します。
このような境界条件はノイマン境界条件ともいわれディレクレ境界条件と共によく使われます。
静電場の問題では周期的な構造を持った誘電体などを扱うことがありますが、このような場合はこの周期性を利用して解析する領域を小さくすることが出来ます。
下の図は2次元の周期的な構造物の例ですが、周期性を利用して右の図のように破線で囲まれた領域を取り出して解析領域とすることが出来ます。
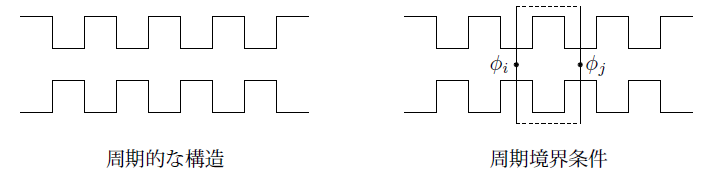
周期境界条件は領域の左右に実線で示している境界線に適用します。周期的に対応する節点のポテンシャルをすべて等しいとします。
図には例えとして節点 $i$ と $j$ のポテンシャルを示しています。
\begin{equation}
\phi_i=\phi_j \notag
\end{equation}
ディレクレ境界条件ではポテンシャルの値が分かっていたので対応する列を右辺に移項したのですが、この場合は二つの未知数が等しいので、これに対応する列を次のように足しこみます。
\begin{equation}
k_{k,i}\phi_i+k_{k,j}\phi_j=(K_{k,i}+K_{k,j})\phi_i \hspace{10mm} (k=1\cdots n) \notag
\end{equation}
ただし方程式の次数を $n$ とします。これによって係数行列は $n$ 行 $n-1$ 列になりますが、列に関しても、
\begin{equation}
k_{i,k}\phi_i+k_{j,k}\phi_k=(K_{i,k}+K_{j,k})\phi_k \hspace{10mm} (k=1\cdots n) \notag
\end{equation}
このように足しこみます。これにより係数行列とベクトルは次のようになります。
\begin{equation}
\begin{bmatrix}
k_{1,1} & \cdots & k_{1,i}+k_{1,j} & \cdots & k_{1,n} \\
\vdots & \ddots & \vdots & \ddots & \vdots \\
k_{i,1}+k_{j,1} & \cdots & k_{i,i}+k_{i,j}+k_{j,i}+k_{j,j} & \cdots & k_{i,n}+k_{j,n} \\
\vdots & \ddots & \vdots & \ddots & \vdots \\
k_{n,1} & \cdots & k_{n,i}+k_{n,j} & \cdots & k_{n,n}
\end{bmatrix}
\hspace{10mm}
\begin{bmatrix}
f_1 \\
\vdots \\
f_i+f_j \\
\vdots \\
f_n
\end{bmatrix} \notag
\end{equation}
このようにして周期境界上の全ての節点について対応する行と列を縮小することによって周期境界条件を適用することが出来ます。
技術情報 Techinicalinfo
- ホーム
- 技術情報
- 【技術情報】有限要素法入門
- 1.5 静電場の境界条件
【技術情報】有限要素法入門
