電荷の受ける力によって電場や磁場の存在を知ることができることと、これらの力によって電場や磁場を定量的に測定ができることを前回示しました。それではこのような電場や磁場はどのようにしてできるのでしょうか。今回は電場がどのように作られるかを見ていきます。
今、二つの電荷のみが存在する空間について考えます。実際の空間にはいろいろなものが存在しますのでこのような空間を想定できないというのであれば、着目している二つの電荷に影響を及ぼすものが十分遠くに離れていると考えてもかまいません。どちらの電荷も互いに静止しているとします。この時この二つの電荷は互いに力を及ぼすことが経験的にわかっています。一つの電荷に着目しますと、静止している状態で力を受けるわけですから、その電荷のある場所に電場が存在することが分かります。この空間には二つの電荷しかないわけですからこの電場はもう一つの電荷によって作られたものであると考えることができます。このことはどちらの電荷についても同じように言えますのでこの二つの電荷はどちらも電場を発生させていることが分かります。
電荷が電場を作ることは次のように考えても分かります。電荷が電場によって力を受けることは、作用反作用の法則より、この電荷が逆に電場の発生源に力を及ぼすことになります。この電場の発生源が受ける力とはどのような力でしょうか。接触力でないことは明らかです。なぜなら、電荷は他の物体と接触しなくても力を受けることができるので接触力によって反作用を与えることができないからです。また重力でもありません。この力は電場や磁場によるものと考えるのが妥当です。さらにこの力が磁場によるものでないことも簡単に示すことができます。ローレンツ力により、電場が電荷に及ぼす力は電荷の運動によらないわけですが、このことはこの電荷と電場の発生源との相対速度によっては電荷の受ける力も、その反作用である電場の発生源が受ける力も変化しないことになります。一方磁場による力は電荷の運動によって変化しますので電場の発生源の受ける力は電場によるものとなります。
それでは電荷の作る電場を定量的に表現することを考えます。これに関しては経験的な事実をまとめたクーロンの法則があります。もともとクーロンの法則は電荷どうしに働く力に関して得られたものですが、ここでは電荷の作る電場についての法則として表現します。1クーロンの電荷が1メートル離れた場所に作る電場の大きさは、
\begin{equation}
8.987551787\times10^9 \hspace{5mm} [\mathrm{N}/\mathrm{Q}] \notag
\end{equation}
となります。ここで、$[\mathrm{N}/\mathrm{Q}]$ つまり、ニュートン/クーロンはあまり使わない単位なので電場の単位としてボルト/メートル、$[\mathrm{V}/\mathrm{m}]$ を今後使います。この単位は $[\mathrm{N}/\mathrm{Q}]$ と同じで、
\begin{equation}
1\,[\mathrm{V}/\mathrm{m}]=1\,[\mathrm{N}/\mathrm{Q}] \notag
\end{equation}
となります。すなわち1クーロンの電荷が電場から受けたときその大きさが1ニュートンになる場合その電場の強さが $1\,\mathrm{V}/\mathrm{m}$ となるわけです。
クーロンの法則では電荷の作る電場の大きさは、電荷の大きさに比例し、電荷からの距離の平方に逆比例し、電場の方向は電荷からその電場の作られた点に向いた方向となります。したがって大きさ $Q$ の電荷が $r$ メートル離れた場所に作る電場は次のようになります。
\begin{equation}
\boldsymbol{E}=8.987551787\times 10^9\times\frac{Q}{r^2}\frac{\boldsymbol{r}}{r} \hspace{5mm} [\mathrm{V}/\mathrm{m}] \tag*{$(3-1)$}
\end{equation}
ここにベクトル $\boldsymbol{r}$ は電荷のある場所を原点としたときの電場の観測点までの位置ベクトルです。これより、電荷 $Q$ が正の値を持てば電荷から放射状に外向きの電場が作られ、電荷 $Q$ が負の値を持てば電荷の方向を向いた電場が作られることが分かります。この式を後から便利なように、次のようにかき換えておきます。
\begin{equation}
\boldsymbol{E}=\frac{1}{4\pi\epsilon_0}\frac{Q}{r^2}\frac{\boldsymbol{r}}{r} \hspace{5mm} [\mathrm{V}/\mathrm{m}] \tag*{$(3-2)$}
\end{equation}
ここで、
\begin{equation}
\epsilon_0=\frac{1}{4\pi\times 8.987551787\times 10^9}=8.854187818\times 10^{-12} \hspace{5mm} [\mathrm{Q/Vm}] \tag*{$(3-3)$}
\end{equation}
であり、真空の誘電率とよびます。ただしここで $\epsilon_0$ を導入したのはあくまで便宜的なことで、これがなぜ真空の誘電率であるかなど今のところ考える必要はありません。また、$\epsilon_0$ はコンデンサーの静電容量の単位であるファラッド、$[\mathrm{F}]$、
\begin{equation}
1[\mathrm{F}]=1[\mathrm{Q}/\mathrm{V}] \notag
\end{equation}
をつかうと、
\begin{equation}
\epsilon_0=8.854187818\times 10^{-12} \hspace{5mm} [\mathrm{F}/\mathrm{m}] \notag
\end{equation}
となります。
この法則によると1クーロンという電荷は非常に大きな電場を発生させることが分かります。例えば、1クーロンの電荷から1メートル離れた場所に1クーロンの電荷を置けば、この電荷に働く力は、
\begin{equation}
\begin{split}
F&=8.987551787\times 10^9 \hspace{5mm} [\mathrm{N}] \\
&=9.17097121\times 10^8 \hspace{5mm} [\mathrm{KgW}]
\end{split} \notag
\end{equation}
すなわち約90万トンとなります。このことから私たちの身近にある電荷は、1クーロンよりはるかに小さなものであることが分かります。また電流1アンペアは1秒間に1クーロンの電荷を運んでいるわけですが、こちらはそれほど大きな電流でなく身近に接することができます。
ここでこの法則をもう少し違った表現にかきかえます。いくつかの電荷を含んだ空間領域 $V$ を考えます。この空間の境界面を $S$ とすれば次の関係が成立します。
\begin{equation}
\int_S\boldsymbol{E}\cdot\boldsymbol{n}dS=\frac{\sum Q}{\epsilon_0} \tag*{$(3-4)$}
\end{equation}
ここに、$\boldsymbol{n}$ は曲面 $S$ の単位法線ベクトルで、領域 $V$ から外向きの方向にとっています。この関係が成立することは次のようにして示すことができます。領域内の一つの電荷 $Q$ が境界面 $S$ のある微小領域 $\Delta S$ に作る電場に着目します。$\Delta S$ 内では電場は一定であると考えることができますので、この面上での積分は次のようにかくことができます。
\begin{equation}
\int_{\Delta S}\boldsymbol{E}\cdot\boldsymbol{n}dS=\boldsymbol{E}\cdot\boldsymbol{n}\Delta S=E\mathrm{cos}\theta\Delta S \notag
\end{equation}
ここに、$E$ は電場 $\boldsymbol{E}$ の大きさ、$\theta$ は電場の方向と法線ベクトル $\boldsymbol{n}$ のなす角です。今電荷 $Q$ からこの微小面 $\Delta S$ を見たときの立体角を $\Delta\Omega$ とかけば、
\begin{equation}
\Delta\Omega=\frac{\Delta S\mathrm{cos}\theta}{r^2} \notag
\end{equation}
が成立するのが分かりますので、この関係と(3-2)式を使って上の積分をかきなおすと、
\begin{equation}
\begin{split}
\int_{\Delta S}\boldsymbol{E}\cdot\boldsymbol{n}dS=E\mathrm{cos}\theta\Delta S&=\frac{1}{4\pi\epsilon_0}\frac{Q}{r^2}\Delta\Omega r^2 \\
&=\frac{Q}{4\pi\epsilon_0}\Delta\Omega
\end{split} \notag
\end{equation}
となります。これはこの積分が面の向きや電荷からの距離とは関係なく立体角 $\Delta\Omega$ のみによって表すことができることを示しています。したがって、面積分を領域 $V$ を取り囲む面 $S$ について行えば、
\begin{equation}
\int_S\boldsymbol{E}\cdot\boldsymbol{n}dS=\frac{Q}{\epsilon_0} \notag
\end{equation}
が成立します。これは一つの電荷について成り立つ関係ですが、複数の電荷がある場合の電場は各電荷が独立に存在するときの電場を単純に足し合わせたものとなりますから、これより(3-4)式が成立することになります。ここでガウスの発散定理を使って(3-4)式の左辺を変形すると次のようになります。
\begin{equation}
\int_S\boldsymbol{E}\cdot\boldsymbol{n}dS=\int_V\mathrm{div}\boldsymbol{E}dV \notag
\end{equation}
一方この式の右辺は電荷密度を $\rho$ とおけば、
\begin{equation}
\frac{\sum Q}{\epsilon_0}=\int_V\frac{\rho}{\epsilon_0}dV \notag
\end{equation}
となるので、次の積分方程式が成立します。
\begin{equation}
\int_V\bigl(\mathrm{div}\boldsymbol{E}-\frac{\rho}{\epsilon_0}\bigr)dV=0 \notag
\end{equation}
この方程式は任意の領域 $V$ について成り立ちますので、次の微分方程式が得られます。
\begin{equation}
\mathrm{div}\boldsymbol{E}=\frac{\rho}{\epsilon_0} \tag*{$(3-5)$}
\end{equation}
今まで電場は電荷が作るといってきましたが、電場を作るのは電荷だけではありません。ファラデーの電磁誘導の法則によると、変化する磁場が電場を発生させることが分かります。この法則を説明するために磁束という量を導入します。ファラデーは電場や磁場を表すために電気力線や磁力線という概念を導入しました。これは電場や磁場を線で表し、その線の方向が電場や磁場の方向を示し、面を貫く線の密度で場の大きさを表現したものです。ここである閉曲面を考えます。この面を貫く磁力線の総数を磁束とよびます。
ファラデーの法則は、この磁束が時間的に変化すればその面を取り囲むように起電力が発生することを示しています。この法則をもう少し定量的に表現するために磁束 $\Phi$ を次のようにかきます。
\begin{equation}
\Phi=\int_S\boldsymbol{B}\cdot\boldsymbol{n}dS \tag*{$(3-6)$}
\end{equation}
ここに、$\boldsymbol{n}$ は曲面 $S$ の単位法線ベクトルです。
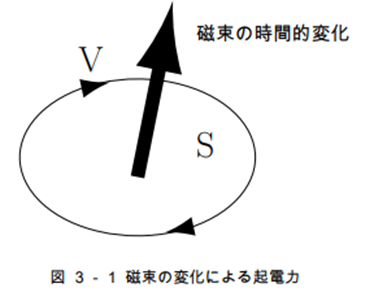
またこの面の周囲の起電力 $V$ は、この面の境界である閉曲線 $l$ についての電場の周回積分として次のように表すことができます。
\begin{equation}
V=\oint_l\boldsymbol{E}\cdot d\boldsymbol{l} \tag*{$(3-7)$}
\end{equation}
ただし、$d\boldsymbol{l}$ は曲線 $l$ の方向にとった線素です。
これらの量を使うとファラデーの法則は次のように表現されます。
\begin{equation}
V=-\frac{d\Phi}{dt} \tag*{$(3-8)$}
\end{equation}
これを電場と磁場の関係でかくと、(3-6)(3-7)式より、
\begin{equation}
\oint_l\boldsymbol{E}\cdot d\boldsymbol{l}=-\frac{\partial}{\partial t}\int_S\boldsymbol{B}\cdot{n}dS \tag*{$(3-9)$}
\end{equation}
となります。この式は、磁場の時間変化によって電場が発生することを示しています。ここでベクトル解析の関係を使ってこの式の左辺を次のようにかきなおします。
\begin{equation}
\oint_l\boldsymbol{E}\cdot d\boldsymbol{l}=\int_S\mathrm{rot}\boldsymbol{E}\cdot\boldsymbol{n}dS \notag
\end{equation}
これを使って(3-9)式を変形すれば、次のようになります。
\begin{equation}
\int_S\mathrm{rot}\boldsymbol{E}\cdot\boldsymbol{n}dS=-\frac{\partial}{\partial t}\int_S\boldsymbol{B}\cdot\boldsymbol{n}dS \notag
\end{equation}
閉曲面 $S$ は時間的に変化しないと考えているので、この式は次のように変形できます。
\begin{equation}
\int_S\bigl(\mathrm{rot}\boldsymbol{E}+\frac{\partial\boldsymbol{B}}{\partial t}\bigr)\cdot\boldsymbol{n}dS=0 \notag
\end{equation}
この式つまりファラデーの法則はどのような閉曲面に対しても成り立ちますので、結局次のような微分方程式が成立します。
\begin{equation}
\mathrm{rot}\boldsymbol{E}=-\frac{\partial\boldsymbol{B}}{\partial t} \tag*{$(3-10)$}
\end{equation}
この式は磁場が時間的に変化するとその周りに電場が発生することを示しています。
今回は電場が何によって生ずるかということについて考え、電荷によるもの、すなわち(3-5)式と、磁場の時間的な変化によるもの、すなわち(3-10)式があることが分かりました。電場の原因はこの二つの場合ですべて表すことができます。次回は磁場がどのように作られるかについて議論します。
技術情報 Techinicalinfo
- ホーム
- 技術情報
- 【技術情報】電磁気学入門
- 3. 電場の発生
【技術情報】電磁気学入門
