前回は、電荷や磁場の時間的変化によってどのように電場が発生するかを見てきましたが、今回は磁場がどのように作られるかを考えます。磁場の存在は磁石に働く力によって身近に知ることができます。したがって磁場の発生を磁石から考えていくこともできますが、磁石について議論するためには磁性体についての知識が必要になります。ところで磁場は電流によっても作られることが分かってますので、ここではまず電流による磁場の発生について考えていくことにして、磁石による磁場の発生については磁性体の話をした後で述べたいと思っています。実際、電流が磁場を作ることは、ファラデーが電磁誘導の法則を発見する前に、アンペールにより発見されアンペールの法則として定量的にまとめられています。
今ある曲面を $S$ としてこの面を通して流れる電流を $i$ とすれば、$S$ の周りに図4-1のような磁場が作られます。
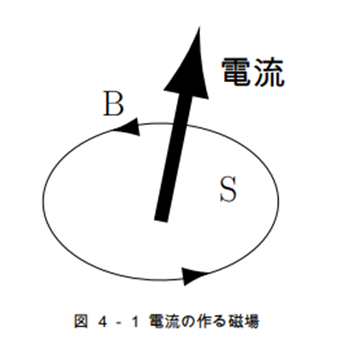
この法則はファラデーの法則と同じように磁場の周回積分として次のようにかくことができます。
\begin{equation}
\oint_l\boldsymbol{B}\cdot d\boldsymbol{l}=ki \tag*{$(4-1)$}
\end{equation}
ここで $l$ は閉曲面 $S$ を取り囲む境界線で電流の流れる向きに対して右ねじ方向に周回積分をとるものとします。また、$k$ は定数です。この法則から電流が分かっていればその電流の作る磁場を計算することができます。簡単な例として無限に長い線電流を考えます。また閉曲面 $S$ としてこの電流が中心を通る半径 $r$ の円に囲まれた面を考えますと、(4-1)式は次のようにかくことができます。
\begin{equation}
2\pi rB=ki \notag
\end{equation}
これより、この電流から $r$ メートル離れた位置の磁場の大きさは、
\begin{equation}
B=\frac{ki}{2\pi r} \tag*{$(4-2)$}
\end{equation}
となります。この式を使って定数 $k$ を知ることができます。ここで、次に示す電流の単位アンペアーの定義を思い出してください。まず1メートルの間隔で平行に置かれた2本の電線を考えます。どちらも同じ大きさの電流が同じ方向に流れているとき、互いに引き付けあう力が生じます。その力が電線1メートルあたり、
\begin{equation}
2\times10^{-7} \hspace{2mm} ニュートン \notag
\end{equation}
のとき、この電流の大きさを1アンペアと定義します。1アンペアの電流が1秒間に運ぶ電気量つまり電荷を1クーロンと定義します。
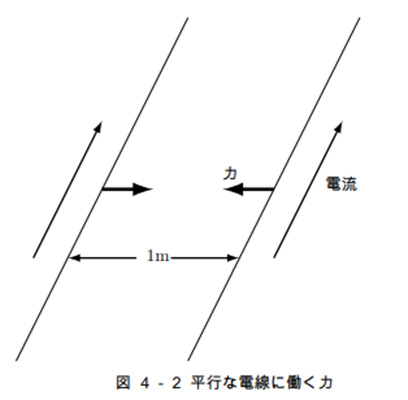
この定義とローレンツ力の計算から定数 $k$ を計算するのですが、一般に $r$ メートルの間隔で平行に置かれたどちらも $i$ アンペアの電流が同じ方向に流れる2本の電線を考えますと、一方の電線がもう一本の電線の位置に作る磁場は(4-2)式となりますので、ローレンツ力よりこの電線が受ける力は次のようになります。
\begin{equation}
f=\frac{ki^2}{2\pi r} \tag*{$(4-3)$}
\end{equation}
ここで電流1アンペアー、電線間の距離を1メートルとおいたときにこの力が $2\times 10^{-7}$ ニュートンとなりますので、次の式が成立します。
\begin{equation}
\frac{k}{2\pi}=2\times 10^{-7} \notag
\end{equation}
したがって、
\begin{equation}
k=4\pi\times 10^{-7} \hspace{2mm} [\mathrm{Nm/A^2}] \notag
\end{equation}
となります。これからこの定数のことを真空の透磁率とよび $\mu_0$ とかくことにします。このようにかくのはあくまで便宜的なことなので、なぜこれが真空の透磁率であるかということをここで考える必要はありません。
今単位面積を流れる電流密度をベクトルで $\boldsymbol{J}$ とかけば電流 $i$ は次のように表すことができます。
\begin{equation}
i=\int_S\boldsymbol{J}\cdot\boldsymbol{n}dS \tag*{$(4-4)$}
\end{equation}
ここに $\boldsymbol{n}$ は曲面 $S$ の単位法線ベクトルです。また(4-1)式の左辺はベクトル解析の関係を使って次のようにかきなおすことができます。
\begin{equation}
\oint_l\boldsymbol{B}\cdot d\boldsymbol{l}=\int_S\mathrm{rot}\boldsymbol{B}\cdot\boldsymbol{n}dS \notag
\end{equation}
これより(4-1)式は、
\begin{equation}
\int_S\mathrm{rot}\boldsymbol{B}\cdot\boldsymbol{n}dS=\mu_0\int_S\boldsymbol{J}\cdot\boldsymbol{n}dS \notag
\end{equation}
となります。この式を変形すれば次式が得られます。
\begin{equation}
\int_S\bigl(\mathrm{rot}\boldsymbol{B}-\mu_0\boldsymbol{J}\bigr)\cdot\boldsymbol{n}dS=0 \notag
\end{equation}
この式はどのような閉曲面についても成り立ちますので、結局次の微分方程式が成立します。
\begin{equation}
\mathrm{rot}\boldsymbol{B}=\mu_0\boldsymbol{J} \tag*{$(4-5)$}
\end{equation}
この式は電流があるとその周りに回転磁場が発生することを示しています。ただし、この式からだけでは電流密度が分かっていても磁場を決定することはできません。それを示すために、仮に異なった磁場が同時に(4-5)式を満たすことが可能であることを示します。今(4-5)式をみたす異なった二つの磁場を $\boldsymbol{B}_1$ と $\boldsymbol{B}_2$ とすれば次式が成立します。
\begin{equation}
\begin{split}
&\mathrm{rot}\boldsymbol{B}_1=\mu_0\boldsymbol{J} \\
&\mathrm{rot}\boldsymbol{B}_2=\mu_0\boldsymbol{J}
\end{split} \notag
\end{equation}
両者の差をとれば、
\begin{equation}
\mathrm{rot}(\boldsymbol{B}_1-\boldsymbol{B}_2)=0 \notag
\end{equation}
となりますが、ベクトル解析の関係から回転をとってゼロとなるベクトルは任意のスカラー関数の勾配として表されますので、次の関係が成り立ちます。
\begin{equation}
\boldsymbol{B}_1-\boldsymbol{B}_2=\mathrm{grad}f \notag
\end{equation}
ただし $f$ は任意のスカラー関数です。このように(4-5)式だけからでは磁場を一意に決定することはできません。そこで、この式の両辺の発散をとりますと、
\begin{equation}
\mathrm{div}\boldsymbol{B}_1-\mathrm{div}\boldsymbol{B}_2=\mathrm{div}\mathrm{grad}f \notag
\end{equation}
となり、ここで磁場の発散が決まっていればこの式の左辺はゼロとなります。すなわち、
\begin{equation}
\mathrm{div}\boldsymbol{B}_1=\mathrm{div}\boldsymbol{B}_2 \notag
\end{equation}
であれば、
\begin{equation}
\mathrm{div}\mathrm{grad}f=\Delta f=0 \notag
\end{equation}
となるので、例えば無限遠で両方の磁場が等しい場合、全領域でこのスカラー関数の値が一定となるので $\boldsymbol{B}_1$ と $\boldsymbol{B}_2$ は等しくなり磁場を決定することができます。磁場の発散を決定する法則をここで決定する必要があるわけですが、これについては経験的に次の簡単な関係が知られています。
\begin{equation}
\mathrm{div}\boldsymbol{B}=0 \tag*{$(4-6)$}
\end{equation}
(4-5)式と(4-6)式から磁場を決定することができます。ただし無限遠で磁場はゼロになるものとします。(4-6)式より、磁場はあるベクトル場 $\boldsymbol{A}$ の回転として、
\begin{equation}
\boldsymbol{B}=\mathrm{rot}\boldsymbol{A} \tag*{$(4-7)$}
\end{equation}
とかくことができます。この式を(4-5)式に代入すると次式が得られます。
\begin{equation}
\mathrm{rot}\mathrm{rot}\boldsymbol{A}=\mu_0\boldsymbol{J} \notag
\end{equation}
ベクトル解析の関係、
\begin{equation}
\mathrm{rot}\mathrm{rot}=\mathrm{grad}\mathrm{div}-\Delta \notag
\end{equation}
を使うとこの式は、
\begin{equation}
\mathrm{grad}\mathrm{div}\boldsymbol{A}-\Delta\boldsymbol{A}=\mu_0\boldsymbol{J} \notag
\end{equation}
と変形されます。(4-7)式の定義の任意性からベクトル場 $\boldsymbol{A}$ に次の条件を与えることができます。
\begin{equation}
\mathrm{div}\boldsymbol{A}=0 \tag*{$(4-8)$}
\end{equation}
これより次のポアソン方程式が得られます。
\begin{equation}
\Delta\boldsymbol{A}=-\mu_0\boldsymbol{J} \tag*{$(4-9)$}
\end{equation}
この式は無限遠で場がゼロとなる条件で解くことができて、
\begin{equation}
\boldsymbol{A}(\boldsymbol{x})=\int_V\frac{\mu_0}{4\pi}\frac{\boldsymbol{J}(\boldsymbol{x}^\prime)}{|\boldsymbol{x}-\boldsymbol{x}^\prime|}dV \tag*{$(4-10)$}
\end{equation}
となります。従って磁場は次のように表されます。
\begin{equation}
\begin{split}
\boldsymbol{B}(\boldsymbol{x})&=\mathrm{rot}\int_V\frac{\mu_0}{4\pi}\frac{\boldsymbol{J}(\boldsymbol{x}^\prime)}{|\boldsymbol{x}-\boldsymbol{x}^\prime|}dV \\
&=\int_V\frac{\mu_0}{4\pi}\frac{\boldsymbol{J}(\boldsymbol{x}^\prime)\times(\boldsymbol{x}-\boldsymbol{x}^\prime)}{|\boldsymbol{x}-\boldsymbol{x}^\prime|^3}dV
\end{split} \tag*{$(4-11)$}
\end{equation}
このように電流がすべて既知であれば磁場を計算することができることになります。ただしこれはあくまで磁性体が存在しない場合の話であり、磁性体が存在する場合には磁性体も磁場を作るため(4-11)式のように簡単には磁場の計算ができなくなります。
今までは、電荷と電流のみが存在する場合の電場や磁場を調べてきましたが、次回は誘電体や磁性体について議論していくつもりです。
技術情報 Techinicalinfo
- ホーム
- 技術情報
- 【技術情報】電磁気学入門
- 4. 磁場の発生
【技術情報】電磁気学入門
