電磁鋼板などの軟磁性体の磁気特性は、ヒステリシスを除けば自由エネルギーにより精度よく決定できます。
これはばねにつながれた物体の変位が物体にかかる力によって決まることと同様に考えることが出来ます。ばね定数を $k$ とし、自然長からの変位を $x$ とすればばねのポテンシャルエネルギー $E$ は、
\begin{equation}
E(x)=\frac{1}{2}kx^2 \notag
\end{equation}
ですからばねにかかる力 $f$ と変位の関係は次のようになります。
\begin{equation}
f=\frac{dE}{dx}=kx \tag*{$(3.5-1)$}
\end{equation}
これは磁性体の単位体積当たりの自由エネルギーと磁場の関係、
\begin{equation}
\boldsymbol{H}=\frac{\partial}{\partial\boldsymbol{B}}F(T,\boldsymbol{B}) \tag*{$(3.5-2)$}
\end{equation}
と対応させることが出来ます。
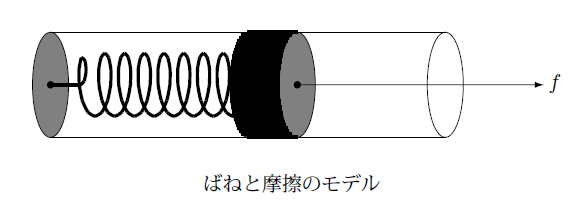
図のようにシリンダーの中に外形がこのシリンダーの内径と同じ円柱形の物を入れ、シリンダーの端部とばねで結びます。
この物体に図のように力をかけると、摩擦がなければ(3.5-1)式にしたがって変位します。
ところがシリンダーの内面と物体の側面の間に摩擦があると、ばねからの力以外に摩擦力 $f_h$ を受けるので(3.5-1)式は次のように修正する必要があります。
\begin{equation}
f-f_h=\frac{dE}{dx}=kx \tag*{$(3.5-3)$}
\end{equation}
この摩擦力は次のように決まります。今変位を $x$、最大摩擦力を $f_c$ とすれば、力の範囲が、
\begin{equation}
kx-f_c\le f \le kx+f_c \notag
\end{equation}
のとき変位は摩擦力のため変化せず、加わった力とばねの力の合計を摩擦力がキャンセルするように働きます。したがってこのときは、
\begin{equation}
f_h=f \notag
\end{equation}
です。またこの範囲以外の場合、最大摩擦力となるので次のようになります。
\begin{equation}
f_h=f_c \notag
\end{equation}
これを示したのが次の図の左のグラフです。
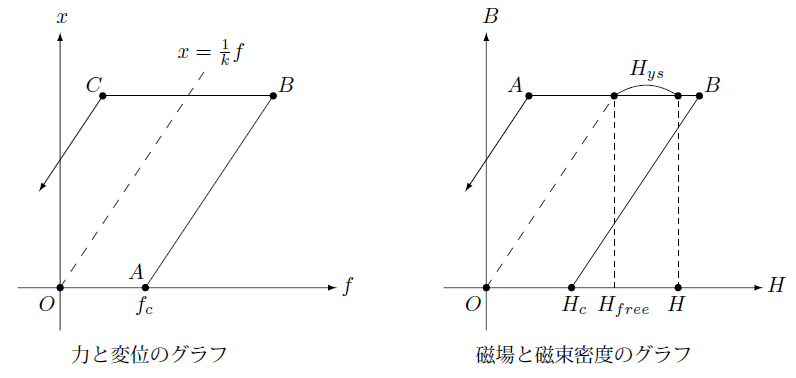
まず力がかかっていないとき物体の変位はゼロでそれを点 $O$ で示しました。力を少しずつ増やしていくと、力が最大摩擦力 $f_c$ より小さいとき変位はゼロを保ち横軸上を動きます。点 $A$ に達し、さらに $f_c$ より大きくなると変位は増加し、点 $B$ に達します。次に力を徐々に小さくしていくと、やはり摩擦力があるので点 $C$ までは変位は変化しないで横軸に平行に移動します。
さらに力を小さくすると図のように変位は減少していきます。このようにばねの力だけではなく摩擦力が働くと、力と変位の関係はヒステリシスを示すことが分かります。
磁性体の磁化特性の場合、力に対応するのが磁場で、変位に対応するのが磁束密度です。そこでこの摩擦力に対応するものとしてヒステリシス磁場 $\boldsymbol{H}_{ys}$ を導入すると、(3.5-3)式に対応して(3.5-2)式は次のように修正されます。
\begin{equation}
\boldsymbol{H}-\boldsymbol{H}_{ys}=\frac{\partial}{\partial\boldsymbol{B}}F(T,\boldsymbol{B}) \tag*{$(3.5-4)$}
\end{equation}
磁束密度を固定して考えると、自由エネルギーから定まる磁場、
\begin{equation}
\boldsymbol{H}_{free}=\frac{\partial F}{\partial\boldsymbol{B}} \tag*{$(3.5-5)$}
\end{equation}
を中心に磁束密度が変化しない領域ができ、磁場がこの範囲にいるとき磁束密度は変化しません。
上の右の図の $AB$ の区間で示した領域です。
そこでこの領域を指定するために通常の保磁力という概念を拡張して、新たに磁束密度に依存する保磁力関 $H_c(\boldsymbol{B})$ を定義します。
この関数を使うと、この磁束密度が変化しない領域の境界面の磁場を次のように表すことが出来ます。
\begin{equation}
\boldsymbol{H}=\boldsymbol{H}_{free}+H_c(\boldsymbol{B})\frac{\boldsymbol{H}-\boldsymbol{H}_{free}}{|\boldsymbol{H}-\boldsymbol{H}_{free}|} \notag
\end{equation}
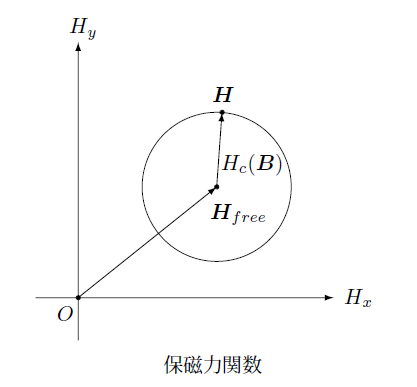
この右辺第2項がこのような形をしているのは保磁力関数をスカラーとして定義したからで、領域の中心とした $\boldsymbol{H}_{free}$ から境界面にある点 $\boldsymbol{H}$ 方向の磁場までの距離が保磁力関数となっていることを示しています。
この様子を2次元の場合について次の図に示します。
したがって磁場がこの領域内部にあるとき、ヒステリシス磁場は、
\begin{equation}
\boldsymbol{H}_{ys}=\boldsymbol{H}-\boldsymbol{H}_{free} \notag
\end{equation}
で、領域外の場合は、
\begin{equation}
\boldsymbol{H}_{ys}=H_c(\boldsymbol{B})\frac{\boldsymbol{H}-\boldsymbol{H}_{free}}{|\boldsymbol{H}-\boldsymbol{H}_{free}|} \notag
\end{equation}
となります。
注意しなければならないのは保磁力関数が磁場の関数ではなく磁束密度の関数であるということで、(3.5-5)式で定義される領域中心 $\boldsymbol{H}_{free}$ における磁束密度に依存します。
これより(3.4-9)式は次のように修正されます。
\begin{equation}
\int_V\delta\boldsymbol{A}\cdot\bigl\{\mathrm{rot}\bigl(\frac{\partial F}{\partial\boldsymbol{B}}+\boldsymbol{H}_{ys}\bigr)-\boldsymbol{J}\bigr\}dV=0 \tag*{$(3.5-6)$}
\end{equation}
ここでこのヒステリシス磁場 $\boldsymbol{H}_{ys}$ をどのように求めるかを説明します。
\begin{equation}
\boldsymbol{H}=\frac{\partial F(\boldsymbol{B})}{\partial\boldsymbol{B}}+\boldsymbol{H}_{ys} \notag
\end{equation}
なので現時点の $\boldsymbol{H}_{free}$ と磁場 $\boldsymbol{H}$ が分かっていればこの式からヒステリシス磁場は簡単に求まります。
ところが、この磁場は制御変数であるにもかかわらず(3.5-6)式を解く段階ではわかっていません。
そこでこのヒステリシス磁場を繰り返し計算によって解くことを考えます。
あるステップに着目して前ステップにおける自由エネルギーから定まる磁場を $\boldsymbol{H}_{free}$ とし、(3.5-6)式を解いて得られるこの磁場を、
\begin{equation}
\frac{\partial F(\boldsymbol{B})}{\partial\boldsymbol{B}}=\boldsymbol{H}_F \notag
\end{equation}
とします。
これと現時点のヒステリシス磁場 $\boldsymbol{H}_{ys}$ から新しい磁場を次のように計算します。
\begin{equation}
\boldsymbol{H}=\boldsymbol{H}_F+\boldsymbol{H}_{ys}=\frac{\partial F(\boldsymbol{B})}{\partial\boldsymbol{B}}+\boldsymbol{H}_{ys} \notag
\end{equation}
これから前ステップの $\boldsymbol{H}_{free}$ からの変化量 $\Delta\boldsymbol{H}$ を次のように計算します。
\begin{equation}
\Delta\boldsymbol{H}=\boldsymbol{H}-\boldsymbol{H}_{free}=\boldsymbol{H}_F+\boldsymbol{H}_{ys}-\boldsymbol{H}_{free} \tag*{$(3.5-7)$}
\end{equation}
そして次のようにヒステリシス磁場を計算します。
\begin{equation}
\begin{split}
&\boldsymbol{H}_{ys}^{new}=\Delta\boldsymbol{H} \hspace{17mm} |\Delta\boldsymbol{H}|\le H_c \\
&\boldsymbol{H}_{ys}^{new}=H_c\frac{\Delta\boldsymbol{H}}{|\Delta\boldsymbol{H}|} \hspace{10mm} |\Delta\boldsymbol{H}|>H_c
\end{split} \tag*{$(3.5-8)$}
\end{equation}
これらの操作を繰り返すことによって(3.5-7)式の左辺がヒステリシス磁場 $\boldsymbol{H}_{ys}$ と一致させます。
収束すれば磁場 $\boldsymbol{H}_F$ は自由エネルギーから定まる $\boldsymbol{H}_{free}$ と等しくなります。
次のステップに進む前に自由エネルギーから定まる磁場を次のように更新します。
\begin{equation}
\begin{split}
&\boldsymbol{H}_{free}^{new}=\boldsymbol{H}_{free}^{old} \hspace{30mm} |\Delta\boldsymbol{H}|\le H_c \\
&\boldsymbol{H}_{free}^{new}=(|\Delta\boldsymbol{H}|-H_c)\frac{\Delta\boldsymbol{H}}{|\Delta\boldsymbol{H}|} \hspace{10mm} |\Delta\boldsymbol{H}|>H_c
\end{split} \notag
\end{equation}
ここまでは軟磁性体のヒステリシスについて考えてきたので保磁力が小さく磁場がそれより小さいときは磁束密度が変化しないと考えてきました。
しかし硬磁性体のヒステリシスの場合、磁場が保磁力より小さいときは磁束密度ではなく磁化が一定となります。
したがって次のように修正する必要があります。
磁化が一定となるように磁場が $\Delta\boldsymbol{H}$ 変化すると磁束密度は $\mu_0\Delta\boldsymbol{H}$ だけ変化します。
保磁力関数の中心磁場 $\boldsymbol{H}_{free}$ に対応する磁束密度を $\boldsymbol{B}_{free}$ とすれば新たな磁束密度は、
\begin{equation}
\boldsymbol{B}_{free}^\prime=\boldsymbol{B}_{free}+\mu_0\Delta\boldsymbol{H} \notag
\end{equation}
となり、ヒステリシス磁場の起点はこの磁束密度に対応する磁場 $\boldsymbol{H}_{free}^\prime$ となります。これより(3.5-7)式は次のように修正する必要があります。
\begin{equation}
\begin{split}
\Delta\boldsymbol{H}&=\boldsymbol{H}_F+\boldsymbol{H}_{ys}-\boldsymbol{H}_{free}-(\boldsymbol{H}_{free}^\prime-\boldsymbol{H}_{free}) \\
&=\boldsymbol{H}_F+\boldsymbol{H}_{ys}-\boldsymbol{H}_{free}^\prime
\end{split} \notag
\end{equation}
それでは次に自由エネルギーと保磁力関数をどのように決定するかについて述べます。
磁性体の自由エネルギーと保磁力関数を磁束密度の関数として与えれば、磁場解析の方程式(3.5-4)式を解くことによってヒステリシスが考慮できます。
それでは測定からどのようにこれらの関数を決定できるかについてお話しします。磁化特性の測定値として磁性体の容易軸方向や圧延方向などから、ある角度をなす方向に測定されたメジャーループの点列が与えられているものとして、上昇時の点列を $H_R$、下降時の点列を $H_L$ とします。
これらの点列から図に示すように平均磁化特性、
\begin{equation}
H_F(B)=\frac{1}{2}(H_R+H_L) \tag*{$(3.5-9)$}
\end{equation}
と上昇時の磁化曲線と下降時の磁化曲線の差、すなわち保磁力関数、
\begin{equation}
H_c(B)=\frac{1}{2}(H_R-H_L) \tag*{$(3.5-10)$}
\end{equation}
を求めます。
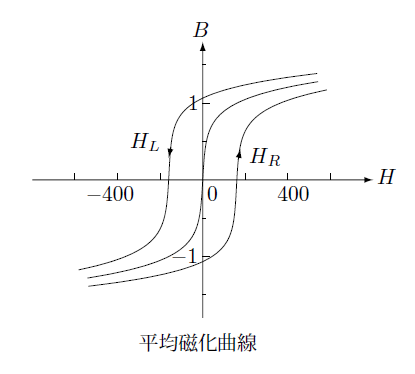
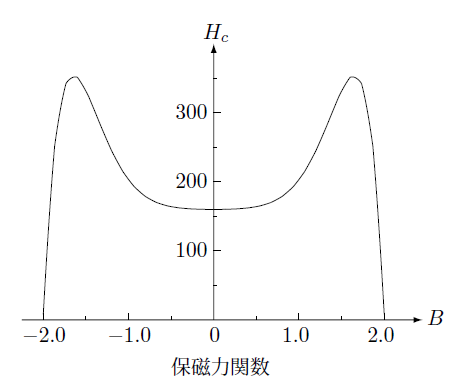
平均磁化曲線が自由エネルギーから決定される(3.5-5)式の磁場であるとし自由エネルギーの磁場の依存性を求めます。
これによって求まった自由エネルギーを下の図に示します。
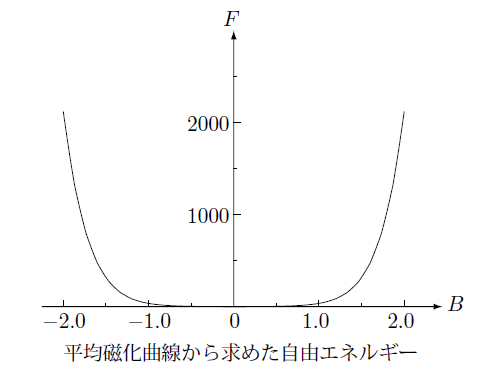
ここで自由エネルギーを測定で求まった(3.5-9)式から決定する方法について述べます。自由エネルギーは、測定された磁束密度の正負について対称なので、磁束密度の偶関数で表現することが出来ます。
\begin{equation}
F(B)=\sum_{n=1}^NC_n^FB^{2n} \tag*{$(3.5-11)$}
\end{equation}
これより、
\begin{equation}
H_F(B)=\frac{\partial}{\partial B}F(B)=\sum_{n=1}^N2nC_n^FB^{2n-1} \notag
\end{equation}
ですから測定を再現できるように最小自乗法を使って係数 $C_n^F$ を決定することが出来ます。
同様に保磁力関数は、
\begin{equation}
H_c(B)=\sum_{n=0}^MC_n^HB^{2n} \tag*{$(3.5-12)$}
\end{equation}
と表現できますので測定値と比較して最小自乗法を使って$C_n^H$を決定することが出来ます。
ここまでは1次元の場合ですが3次元について述べます。まず等方性磁性体の場合は自由エネルギーは磁束密度の方向によらないので磁束密度の絶対値、
\begin{equation}
B=\sqrt{|\boldsymbol{B}|^2} \notag
\end{equation}
を使って次のように表されます。
\begin{equation}
F(\boldsymbol{B})=\sum_{n=1}^NC_n^F(B^2)^n \tag*{$(3.5-13)$}
\end{equation}
これより磁場の $i$ 成分は次のようにかけます。
\begin{equation}
H_i(B)=\frac{\partial F}{\partial B_i}=\sum_{n=1}^N2nC_n^F(B^2)^{n-1}B_i \notag
\end{equation}
さらに磁束密度で微分すれば、
\begin{equation}
\frac{\partial^2F}{\partial B_i\partial B_j}=\sum_{n=1}^N\bigl\{4n(n-1)C_n^F(B^2)^{n-1}\frac{B_iB_j}{B^2}
+2nC_n^F(B^2)^{n-1}\delta_{ij}\bigr\} \notag
\end{equation}
となります。
磁性体のヒステリシスの測定は、磁化容易軸とそれに直角方向など限られた方向でのみ行われるのが実情でこれらのデータから
自由エネルギや保磁力関数をどのように求めるかを考えます。
例えば磁化容易軸に沿った座標系の座標軸に沿った3方向の測定値がある場合、自由エネルギーは座標成分を添字 $i$ とすればそれぞれの方向に、
\begin{equation}
F(B_i)=\sum_{n=1}^NC_{ni}^FB_i^{2n} \tag*{$(3.5-14)$}
\end{equation}
保磁力関数については、
\begin{equation}
H_c(B_i)=\sum_{n=0}^MC_{ni}^HB_i^{2n} \tag*{$(3.5-15)$}
\end{equation}
と座標軸上の補間関数が求まっています。
ここで簡単のため2次元の場合について考えます。例えば自由エネルギーが $x$ 軸上と $y$ 軸上で与えられている場合、極座標で表すと $0$ 度と $90$ 度だけの値が求まっていることになります。このとき座標軸は特別な方向、つまり磁化容易軸方向や困難軸方向を向いているため $x$ 成分や $y$ 成分の正負を逆にしても対称であるから第一象限の特性が求まればよいことになります。またこの対称性により自由エネルギーの $0$ 度と $90$度 における角度方向の微分はゼロとなります。
そこで磁束密度を次のように極座標で表します。
\begin{equation}
\begin{split}
&B_x=B\mathrm{cos}\theta \\
&B_y=B\mathrm{sin}\theta
\end{split} \notag
\end{equation}
磁束密度が等しい円弧上での自由エネルギーを次のように近似します。
\begin{equation}
F(\theta)=\frac{1}{2}\{F(0)-F(90)\}\mathrm{cos}2\theta+\frac{1}{2}\{F(0)+F(90)\} \notag
\end{equation}
これは自由エネルギーが持っている対称性を再現するもっとも簡単な関数です。ここで、
\begin{equation}
\mathrm{cos}2\theta=\mathrm{cos}^2\theta-\mathrm{sin}^2\theta=\frac{B_x^2-B_y^2}{B^2} \notag
\end{equation}
ですから上の式は、
\begin{equation}
F(\theta)=F(0)\frac{B_x^2}{B^2}+F(90)\frac{B_y^2}{B^2} \notag
\end{equation}
となります。したがって磁束密度の成分の関数でかけば、
\begin{equation}
F(B_x,B_y)=F(B,0)\frac{B_x^2}{B^2}+F(0,B)\frac{B_y^2}{B^2} \tag*{$(3.5-16)$}
\end{equation}
となります。これを3次元に拡張することは簡単で、次のようになります。
\begin{equation}
F(B_x,B_y,B_z)=F(B,0.0)\frac{B_x^2}{B^2}+F(0,B,0)\frac{B_y^2}{B^2}+F(0,0,B)\frac{B_z^2}{B^2} \tag*{$(3.5-17)$}
\end{equation}
ここで座標成分 $x$、$y$、$z$ を数字の $1$、$2$、$3$ で表し、
\begin{equation}
\begin{split}
&F^1(B)=F(B,0,0) \\
&F^2(B)=F(0,B,0) \\
&F^3(B)=F(0,0,B)
\end{split} \notag
\end{equation}
とおけばこの式は次のようにかけます。
\begin{equation}
F(\boldsymbol{B})=\sum_{i=1}^3F^i(B)\frac{B_i^2}{B^2} \notag
\end{equation}
(3.5-14)式を使ってかきなおすと次のようになります。
\begin{equation}
F(\boldsymbol{B})=\sum_{k=1}^3\sum_{n=1}^NC_{kn}^FB^{2n}\frac{B_k^2}{B^2} \notag
\end{equation}
これより磁場の成分は次のようになります。
\begin{equation}
\begin{split}
H_i&=\frac{\partial F}{\partial B_i} \\
&=\sum_{k=1}^3\sum_{n=1}^NC_{kn}^F\{(2n-2)B^{2n-4}B_iB_k^2+2B^{2n-2}B_k\delta_{ik}\}
\end{split} \tag*{$(3.5-18)$}
\end{equation}
さらに磁束密度で微分すると、
\begin{equation}
\begin{split}
\frac{\partial^2F}{\partial B_i\partial B_j}
&=\sum_{k=1}^3\sum_{n=1}^NC_{kn}^F\{(2n-2)(2n-4)B^{2n-6}B_iB_jB_k^2 \\
&+(2n-2)B^{2n-4}B_k^2\delta_{ij} \\
&+2(2n-2)B^{2n-4}(B_jB_k\delta_{ik}+B_iB_k\delta_{jk}) \\
&+2B^{2n-2}\delta_{ik}\delta_{jk}\}
\end{split} \tag*{$(3.5-19)$}
\end{equation}
となります。
同様にして保磁力関数も次のようにかけます。
\begin{equation}
H_c(\boldsymbol{B})=\sum_{i=1}^3H_c^i(B)\frac{B_i^2}{B^2} \notag
\end{equation}
(3.5-15)式を使ってかきなおすと、
\begin{equation}
H_c(\boldsymbol{B})=\sum_{i=1}^3\bigl(C_{i0}^H+\sum_{n=1}^MC_{in}^HB^{2n}\bigr)\frac{B_i^2}{B^2} \tag*{$(3.5-20)$}
\end{equation}
となります。
このようにして自由エネルギーと保磁力関数を使って磁化過程を計算すると下の図のような結果が得られます。
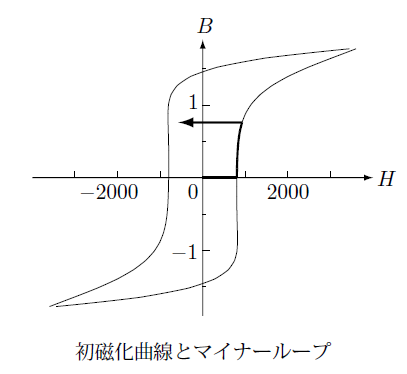
メジャーループに関しては、測定から得られた平均磁化特性と保磁力関数を使っているので測定を再現することが出来るのですが、初磁化曲線やマイナーループの結果は横軸に平行となっており不自然です。
この原因はヒステリシスをばねと摩擦を使ったモデルで物体にかかる力が摩擦力を越えるまでは変位がゼロとしたことです。
このモデルの説明で使った「力と変位のグラフ」を参照してください。
つまり磁場が摩擦力に対応する保磁力を超えるまで磁束密度はゼロを保ちます。
現実の磁性体の初磁化曲線はこのモデルのように磁場が保磁力に達するまで磁束密度がゼロを保つのではなく磁場が保磁力に近づくにつれ徐々に大きくなります。そこでヒステリシス磁場の計算(3.5-8)式を $1$ より小さなパラメータ $\alpha$ を使って次のように修正します。
\begin{equation}
\begin{split}
&\boldsymbol{H}_{ys}^{new}=\Delta\boldsymbol{H}\times\alpha \hspace{17mm} |\Delta\boldsymbol{H}|\le H_c \\
&\boldsymbol{H}_{ys}^{new}=H_c\frac{\Delta\boldsymbol{H}}{|\Delta\boldsymbol{H}|}\times\alpha \hspace{10mm} |\Delta\boldsymbol{H}|>H_c
\end{split} \tag*{$(3.5-21)$}
\end{equation}
まずこのパラメータを一定とした場合に初磁化曲線とマイナーループがどうなるかを示します。
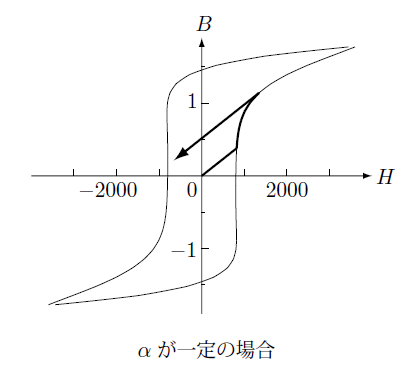
このようにヒステリシス磁場を補正するパラメータ $\alpha$ を一定にした場合マイナーループは直線的な形となりそこでの変化は可逆的になります。そこでこのパラメータを磁場を計算する点で複数用意してそれぞれのパラメータの値を分布させ、その平均でパラメータを表すようにします。
この場合磁場が上昇するときと下降するときにこのパラメータの平均値が異なりヒステリシスを表現できることがわかります。
次の図は、パラメータを中心の周りに分布させたものです。この分布には正規分布や一定の幅に等しく分布することが考えられます。
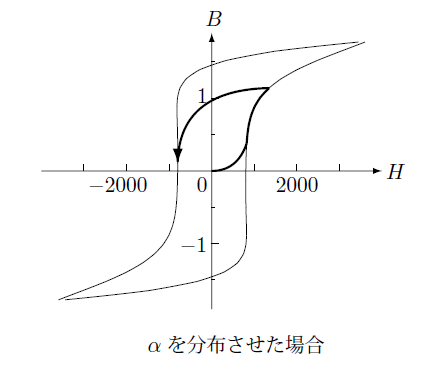
このようにこのモデルではこのパラメータ$\alpha$の分布をどう与えるかによって初磁化曲線とマイナーループが決まります。
したがってできるだけ初磁化曲線を再現するようにパラメータ分布を決定することが重要になります。
技術情報 Techinicalinfo
- ホーム
- 技術情報
- 【技術情報】有限要素法入門
- 3.5 ヒステリシス
【技術情報】有限要素法入門
