1.余分なエネルギーの流れ
表面に電荷が一様に分布している半径R の球がz 方向に一定の速度v で運動しているときの電磁エネルギーの移動について考えます。まず、この球が空間に作る電場のエネルギーは、
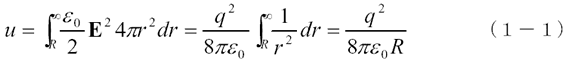
です。前回の球対称な電場の作るポインティングベクトルの計算式、
を使ってz 方向のエネルギーの流れを計算すると、
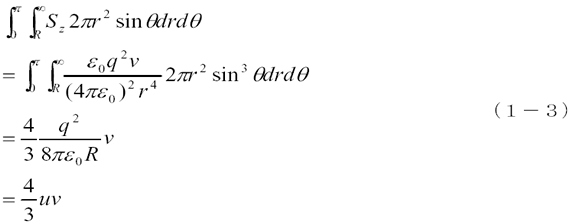
となります。この結果は(1−1)式であらわされる電場のエネルギーが速度v で伝播すると考えたときより、
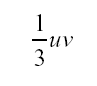
だけ余分なエネルギーの流れがあることになります。
この余分なエネルギーが何であるかというのが今回の問題です。
2.球の内部におけるエネルギーの流れ
前回述べたようにポインティングベクトルは単位体積中の電磁場のエネルギー U、マックスウェルの応力テンソルT を使って
とかけます。今回の問題では電場は球内に存在しないのでポインティングベクトルは球の表面に沿って流れます。
これを次のように二つのエネルギーの流れに分にわけ考えることにします。

S(1)は電場のエネルギーが速度 v で移動していることを表していますので直感的なイメージと合致した流れになっています。ただしこの流れは球表面で不連続に変化します。球表面の単位法線ベクトルをnとしてS(1) との内積をとると次のようになります。
ここにθ は法線ベクトルv と速度 とがなす角であり、この量は球表面からのエネルギーの単位面積あたりの流出量をあらわしています。
同様にnとS(2) との内積をとると次のようになります。
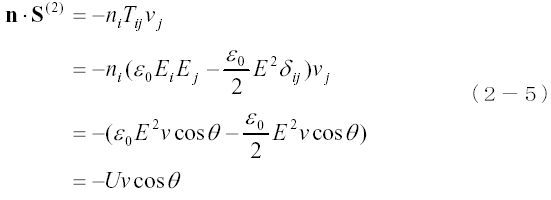
したがって球表面において、
が成立していることが分かります。
エネルギーの流れS(2) だけに着目すると、この流れは一定のエネルギー密度U が球の進行方向から球に流入し反対面から流失していることが分かります。ただし球内部ではこの流れがなくなるように表面で不連続に変化します。
ここで仮に球表面でこのエネルギーの流れが連続するように球内部にも、
のエネルギーの流れがあるものと考えると、球内部で、
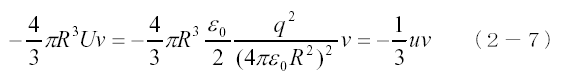
のエネルギーの流れがあることになり、これで余分なエネルギーの流れはキャンセルされます。しかし実際には球の中には電磁場はなくこのような電磁エネルギーの流れもありません。それでは何がこの余分なエネルギーの流れをキャンセルさせているのでしょうか。
実は帯電した球には電荷どうしの反発力によって内部に機械的な応力が生じています。球面単位面積あたりの表面力は、
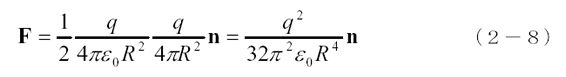
ですからこの球の内部が均質な物質で出来ているとすれば内部応力は、

となります。このような応力を持った物体が速度v で運動した場合、前回、連続体中のエネルギーの移動で述べたように、単位面積あたりのエネルギーの流れp は、
となります。ここで物体の持つ単位体積あたりのエネルギーU mが表面電荷の影響で変化しないとすれば、電荷による応力によって新たに生ずる球内のエネルギーの流れは単位体積あたり、
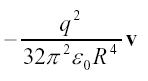
となります。したがって球内部のエネルギーの流れは進行方向に次のようになります。
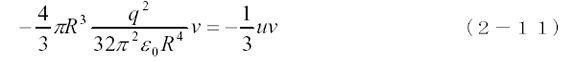
このエネルギーの流れと電磁エネルギーの流れとの和はちょうどuv になるので、球内部のこの応力によるエネルギーの流れを含めて考えれば余分なエネルギーの流れがキャンセルされることになります。
したがってS(2)に(2−10)式の右辺第2項を追加したエネルギーの流れ、
は球の境界でも連続しており次の関係をみたしていることが分かります。
帯電した球の運動にともなう電磁エネルギーの流れを議論してきた中でこのような非電磁的な応力が出てくるのは奇異に感じますが、その昔、電子のモデルにおいてポアンカレが導入したポアンカレ応力に対応していると考えられます。
