強磁性体においては磁場が弱いときは磁場 $\boldsymbol{H}$ と磁束密度 $\boldsymbol{B}$ が比例する傾向にありますが磁場が大きくなると比例しなくなります。
さらに磁場が大きくなり磁性体が飽和してしまうとそれ以上に大きくしても磁化は大きくなりません。
したがって、強磁性体を使う磁場解析においては磁性体の非線形性を扱うことが不可欠になります。
そこでこれからは磁束密度と磁場及び磁化 $\boldsymbol{M}$ の関係、
\begin{equation}
\boldsymbol{H}=\frac{1}{\mu_0}\boldsymbol{B}-\boldsymbol{M} \tag*{$(3.2-1)$}
\end{equation}
を使て話を進めます。ここに $\mu_0$ は真空の透磁率で一定の値をとります。
この磁化は磁場を大きくしていくと最初はそれに比例して大きくなりますがいくらでも大きくなるのではなく飽和磁化 $M_s$ より大きくなることはありません。
その様子を下の図に示しています。
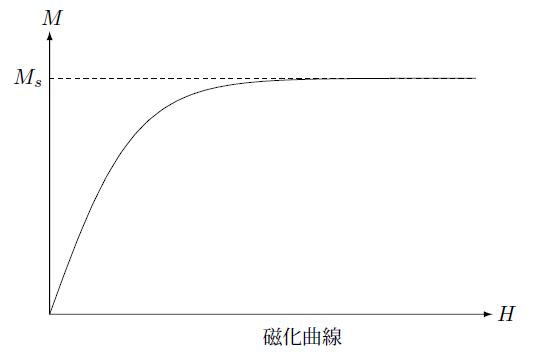
ここでは横軸を磁場 $H$ にとっていますが磁束密度 $B$ にしても同じようになります。磁場解析の場合今まで述べてきたようにベクトルポテンシャルを変数として解いています。したがって磁束密度による依存度を考えることが扱いやすいということで磁化を磁束密度の関数とすることが多いようです。
\begin{equation}
\boldsymbol{M}=\boldsymbol{M}(\boldsymbol{B}) \tag*{$(3.2-2)$}
\end{equation}
ただしこのままでは、それぞれがベクトルどうしの関係なので異方性を含んだ複雑な関係になってしまいます。
そこでここでは等方性磁性体を扱うことにします。
この場合磁化の方向と磁束密度の方向は一致していると考え上の式を次の形に限定します。
\begin{equation}
\boldsymbol{M}=f(|\boldsymbol{B}|)\frac{\boldsymbol{B}}{|\boldsymbol{B}|} \tag*{$(3.2-3)$}
\end{equation}
ここに $|\boldsymbol{B}|$ は磁束密度の絶対値で、磁化の大きさはこの大きさだけで決まるとしています。今後この絶対値を単に $B$ とかくことにします。
この式の両辺の絶対値をとると、
\begin{equation}
M=f(B) \tag*{$(3.2-4)$}
\end{equation}
となりますが、上の図は横軸を磁束密度とすればちょうどこの関係を示したものとみることが出来ます。
この磁化を使ってアンペールの法則(2.1-1)式をかきなおすと次のようになります。
\begin{equation}
\mathrm{rot}\bigl(\frac{1}{\mu_0}\boldsymbol{B}-\boldsymbol{M}\bigr)=\boldsymbol{J} \tag*{$(3.2-5)$}
\end{equation}
この式の磁化に関する項を右辺に移しベクトルポテンシャルを使うと、
\begin{equation}
\mathrm{rot}\frac{1}{\mu_0}\mathrm{rot}\boldsymbol{A}=\boldsymbol{J}+\mathrm{rot}\boldsymbol{M} \tag*{$(3.2-6)$}
\end{equation}
となります。これが(2.1-5)式を非線形磁性体に拡張した式です。この式を見ると右辺の $\mathrm{rot}\boldsymbol{M}$ がちょうど電流と同じ役割をしているのが分かります。したがてこれを磁化電流とよんでいます。また左辺は透磁率 $\mu$ の代わりに真空の透磁率 $\mu_0$ となっており定数なので線形磁性体の場合と同様の議論ができます。
これより(3.1-6)式は次のようにかけます。
\begin{equation}
\int_V\mathrm{rot}\boldsymbol{w}\cdot\frac{1}{\mu_0}\mathrm{rot}\boldsymbol{A}dV
=\int_V\boldsymbol{w}\cdot\boldsymbol{J}dV+\int_V\mathrm{rot}\boldsymbol{w}\cdot\boldsymbol{M}dV+\int_S\boldsymbol{w}\cdot[\boldsymbol{H}\times\boldsymbol{n}]dS \tag*{$(3.2-7)$}
\end{equation}
磁化が分かっていればこの式は線形磁性体の場合と同様にして解くことが出来ます。ところが先ほど述べたようにこの磁化は(3.2-3)式のように磁束密度に依存し磁束密度は解こうとしているベクトルポテンシャルによって決まるのでこのまま解くことはできません。
この方程式を今までやってきたように有限要素法で離散化し連立方程式を作っても右辺のベクトルが未知数であるベクトルポテンシャルに依存するためこのままでは解くことが出来ません。このような方程式のことを非線形方程式といいます。
そこで、非線形方程式を解く方法を一般的に考察します。
まず一変数関数の方程式、
\begin{equation}
f(x)=0 \tag*{$(3.2-8)$}
\end{equation}
これが1次方程式なら簡単に解けますが一般にはそうではありません。非常に複雑な方程式の場合解析的に解くのが困難となります。
このようなとき、この方程式を数値的に解く方法がありますのでここでそれを紹介します。
まず $x$ の値として適当な数 $x^{(1)}$ を決めて初期値とします。出来ればこの方程式の答えに近いものであれば良いのですがそれが分からない場合もあります。
ともかくこの値を上の方程式に入れてやると当然この方程式をみたしません。
\begin{equation}
f(x^{(1)})\ne 0 \notag
\end{equation}
そこで次の方程式をみたすことを考えます。
\begin{equation}
f(x^{(1)}+\Delta x)=0 \notag
\end{equation}
ここで $\Delta x$ は未知の値です。ただし、この方程式を解くことは(3.2-8)式を解くのと変わらないのでこのままでは問題を解決したことになりません。
そこで最初の初期値 $x^{(1)}$ がこの方程式の解に近いとすれば $\Delta x$ は小さな値となりこの式は $\Delta x$ の一次まで展開することができます。
\begin{equation}
f(x^{(1)})+\Delta xf^\prime(x^{(1)})=0 \notag
\end{equation}
ただし、
\begin{equation}
f^\prime(x)=\frac{d}{dx}f(x) \notag
\end{equation}
です。これより、
\begin{equation}
\Delta x=-\frac{f(x^{(1)})}{f^\prime(x^{(1)})} \notag
\end{equation}
となり $\Delta x$ が求まります。
ここでは $\Delta x$ が小さいと仮定したのですが、これは初期値 $x^{(1)}$ がこの方程式の解に近い場合であり一般には小さいとは限りません。
ただその場合でもここで求めた、
\begin{equation}
x^{(2)}=x^{(1)}+\Delta x=x^{(1)}-\frac{f(x^{(1)})}{f^\prime(x^{(1)})} \tag*{$(3.2-9)$}
\end{equation}
は $x^{(1)}$ より答えに近づいていればそれを次の初期値として繰り返していけばいずれ方程式の解に収束していくことが期待できます。
この方法はニュートン法または、ニュートン・ラプソン法と呼ばれています。
この方法の例として、$\sqrt{2}$ を求めてみます。
この値は次の方程式の解です。
\begin{equation}
x^2-2=0 \notag
\end{equation}
まず初期値として $x^{(1)}=1$ とします。これから次々の近似値を(3.2-9)式を使って求めていくと次のようになります。
\begin{equation}
\begin{split}
&x^{(2)}=x^{(1)}-\frac{{x^{(1)}}^2-2}{2x^{(1)}}=1-\frac{1^2-2}{2\cdot1}=1.5 \\
&x^{(3)}=x^{(2)}-\frac{{x^{(2)}}^2-2}{2x^{(2)}}=1.5-\frac{1.5^2-2}{2\cdot1.5}=1.416666667 \\
&x^{(4)}=x^{(3)}-\frac{{x^{(3)}}^2-2}{2x^{(3)}}=1.416666667-\frac{1.416666667^2-2}{2\cdot 1.416666667}=1.414215686 \\
&x^{(5)}=x^{(4)}-\frac{{x^{(4)}}^2-2}{2x^{(4)}}=1.414215686-\frac{1.414215686^2-2}{2\cdot 1.414215686}=1.414213562 \\
\end{split} \notag
\end{equation}
5回の繰り返しで有効桁の範囲で正解が得られました。
このようにこの方法では収束は非常に速いのですが、最初の初期値の選び方によっては収束しないことがあります。
次にこの方法を多変数の場合について拡張します。解くべき方程式は、
\begin{equation}
\begin{split}
f_1(x_1,x_2,&\cdots,x_n)=0 \\
f_2(x_1,x_2,&\cdots,x_n)=0 \\
&\vdots \\
f_n(x_1,x_2,&\cdots,x_n)=0 \\
\end{split} \notag
\end{equation}
です。この場合は初期値も複数あり $(x_1^{(1)},x_2^{(1)},\cdots,x_n^{(1)})$ とします。そこで次の方程式が成り立つように初期値の修正分を求めます。
\begin{equation}
\begin{split}
f_1(x_1^{(1)}+\Delta x_1,x_2^{(1)}&+\Delta x_2,\cdots,x_n^{(1)}+\Delta x_n)=0 \\
f_2(x_1^{(1)}+\Delta x_1,x_2^{(1)}&+\Delta x_2,\cdots,x_n^{(1)}+\Delta x_n)=0 \\
&\vdots \\
f_n(x_1^{(1)}+\Delta x_1,x_2^{(1)}&+\Delta x_2,\cdots,x_n^{(1)}+\Delta x_n)=0 \\
\end{split} \notag
\end{equation}
1変数関数のときと同様に修正分が小さいとして一次まで展開すると、
\begin{equation}
f_i(x_1^{(1)},x_2^{(1)},\cdots,x_n^{(1)})+\sum_{j=1}^n\frac{\partial}{\partial x_j}f_i(x_1^{(1)},x_2^{(1)},\cdots,x_n^{(1)})\Delta x_j=0
\hspace{5mm} (i=1,2,\cdots,n) \notag
\end{equation}
となります。これは $\Delta x_i$ に関する連立方程式なのでこれを解くことによって修正分を求めることができ、
\begin{equation}
x_i^{(2)}=x_i^{(1)}+\Delta x_i \notag
\end{equation}
によって次の近似値を求めることができます。
さて、静磁場解析に話を戻します。(3.2-7)式の左辺は未知数であるベクトルポテンシャル以外は一定の値$\mu_0$しか含んでいないのですが、右辺の磁化は磁束密度 $\boldsymbol{B}$ を通してベクトルポテンシャルに依存します。
ここで右辺の境界積分の項は境界条件として非線形とは関係なく決まっているのでここでは省略します。
いま、ベクトルポテンシャルの初期値を $\boldsymbol{A}$ としてニュートン・ラプソン法での修正分を $\Delta\boldsymbol{A}$ とかくと(3.2-7)式は、
\begin{equation}
\int_V\mathrm{rot}\boldsymbol{w}\cdot\frac{1}{\mu_0}\mathrm{rot}(\boldsymbol{A}+\Delta\boldsymbol{A})dV
=\int_V\boldsymbol{w}\cdot\boldsymbol{J}dV+\int_V\mathrm{rot}\boldsymbol{w}\cdot\boldsymbol{M}(\boldsymbol{B}+\Delta\boldsymbol{B})dV \tag*{$(3.2-10)$}
\end{equation}
となります。ここに、
\begin{equation}
\Delta\boldsymbol{B}=\Delta\mathrm{rot}\boldsymbol{A}=\mathrm{rot}\Delta\boldsymbol{A} \notag
\end{equation}
はベクトルポテンシャルの修正分によって表されます。右辺の磁化は修正分 $\Delta\boldsymbol{B}$ の一次まで展開すると次のようになります。
\begin{equation}
\boldsymbol{M}(\boldsymbol{B}+\Delta\boldsymbol{B})=\boldsymbol{M}(\boldsymbol{B})+\sum_i\frac{\partial\boldsymbol{M}}{\partial B_i}\Delta B_i \notag
\end{equation}
これより上の方程式は、
\begin{equation}
\begin{split}
&\int_V\mathrm{rot}\boldsymbol{w}\cdot\frac{1}{\mu_0}\mathrm{rot}\boldsymbol{A}dV+\int_V\mathrm{rot}\boldsymbol{w}\cdot\frac{1}{\mu_0}\mathrm{rot}\Delta\boldsymbol{A}dV \\
&=\int_V\boldsymbol{w}\cdot\boldsymbol{J}dV+\int_V\mathrm{rot}\boldsymbol{w}\cdot\boldsymbol{M}dV
+\int_V\mathrm{rot}\boldsymbol{w}\cdot\sum_j\frac{\partial\boldsymbol{M}}{\partial B_j}(\mathrm{rot}\boldsymbol{\Delta}\boldsymbol{A})_jdV
\end{split} \notag
\end{equation}
とかけますが、少し変形すると次のようになります。
\begin{equation}
\begin{split}
&\int_V\sum_{ij}(\mathrm{rot}\boldsymbol{w})_i\bigl(\frac{1}{\mu_0}\delta_{ij}-\frac{\partial M_i}{\partial B_j}\bigr)(\mathrm{rot}\Delta\boldsymbol{A})_jdV \\
&=\int_V\boldsymbol{w}\cdot\boldsymbol{J}dV+\int_V\mathrm{rot}\boldsymbol{w}\cdot\boldsymbol{M}dV
-\int_V\mathrm{rot}\boldsymbol{w}\cdot\frac{1}{\mu_0}\mathrm{rot}\boldsymbol{A}dV
\end{split} \tag*{$(3.2-11)$}
\end{equation}
この左辺のカッコの中は次のように変形できます。
\begin{equation}
\frac{1}{\mu_0}\delta_{ij}-\frac{\partial M_i}{\partial B_j}=\frac{\partial}{\partial B_j}\bigl(\frac{1}{\mu_0}B_i-M_i\bigr)
=\frac{\partial H_i}{\partial B_j} \notag
\end{equation}
これより、
\begin{equation}
\sum_{ij}(\mathrm{rot}\boldsymbol{w})_i\bigl(\frac{1}{\mu_0}\delta_{ij}-\frac{\partial M_i}{\partial B_j})(\mathrm{rot}\Delta\boldsymbol{A})_j
=\sum_{ij}(\mathrm{rot}\boldsymbol{w})_i\frac{\partial H_i}{\partial B_j}(\mathrm{rot}\Delta\boldsymbol{A})_j \notag
\end{equation}
ですがここで次の記号を導入します。
\begin{equation}
\mathrm{rot}\boldsymbol{w}\cdot\frac{\partial\boldsymbol{H}}{\partial\boldsymbol{B}}\mathrm{rot}\Delta\boldsymbol{A}\equiv
\sum_{ij}(\mathrm{rot}\boldsymbol{w})_i\frac{\partial H_i}{\partial B_j}(\mathrm{rot}\Delta\boldsymbol{A})_j \tag*{$(3.2-12)$}
\end{equation}
この記号を使うと(3.2-11)式は次のようにかくことができます。
\begin{equation}
\begin{split}
\int_V\mathrm{rot}\boldsymbol{w}\cdot\frac{\partial\boldsymbol{H}}{\partial\boldsymbol{B}}\mathrm{rot}\Delta\boldsymbol{A}dV
=\int_V\boldsymbol{w}\cdot\boldsymbol{J}dV+\int_V\mathrm{rot}\boldsymbol{w}\cdot\boldsymbol{M}dV
-\int_V\mathrm{rot}\boldsymbol{w}\cdot\frac{1}{\mu_0}\mathrm{rot}\boldsymbol{A}dV
\end{split} \tag*{$(3.2-13)$}
\end{equation}
これに有限要素法を適用するために今までやったように領域を要素分割すれば、この方程式は要素積分の和として、
\begin{equation}
\begin{split}
&\sum_n\int_{V_n}\mathrm{rot}\boldsymbol{w}\cdot\frac{\partial\boldsymbol{H}}{\partial\boldsymbol{B}}\mathrm{rot}\Delta\boldsymbol{A}dV \\
&=\sum_n\int_{V_n}\boldsymbol{w}\cdot\boldsymbol{J}dV+\sum_n\int_{V_n}\mathrm{rot}\boldsymbol{w}\cdot\boldsymbol{M}dV
-\sum_n\int_{V_n}\mathrm{rot}\boldsymbol{w}\cdot\frac{1}{\mu_0}\mathrm{rot}\boldsymbol{A}dV
\end{split} \tag*{$(3.2-14)$}
\end{equation}
となります。ただし境界積分の項は煩雑になるので省略していますが線形磁性体のときと同じ扱いをします。
要素内でベクトルポテンシャルとその修正分、そしてベクトル関数 $\boldsymbol{w}$ を次のように補間します。
\begin{equation}
\begin{split}
&\boldsymbol{A}(\boldsymbol{x})=\sum_\alpha\boldsymbol{N}_\alpha(\boldsymbol{x})A^\alpha \\
&\Delta\boldsymbol{A}(\boldsymbol{x})=\sum_\alpha\boldsymbol{N}_\alpha(\boldsymbol{x})\Delta A^\alpha \\
&\boldsymbol{w}(\boldsymbol{x})=\sum_\alpha\boldsymbol{N}_\alpha(\boldsymbol{x})w^\alpha
\end{split} \tag*{$(3.2-15)$}
\end{equation}
ここで次の要素行列と要素ベクトルを次のように定義します。
\begin{equation}
\begin{split}
&K_{\alpha\beta}^{\ast}=\int_{V_n}\mathrm{rot}\boldsymbol{N}_\alpha\cdot\frac{\partial\boldsymbol{H}}{\partial\boldsymbol{B}}\mathrm{rot}\boldsymbol{N}_\beta dV \\
&K_{\alpha\beta}^0=\int_{V_n}\mathrm{rot}\boldsymbol{N}_\alpha\cdot\frac{1}{\mu_0}\mathrm{rot}\boldsymbol{N}_\beta dV \\
&F_\alpha=\int_{V_n}\boldsymbol{N}_\alpha\cdot\boldsymbol{J}dV \\
&M_\alpha=\int_{V_n}\mathrm{rot}\boldsymbol{N}_\alpha\cdot\boldsymbol{M}dV
\end{split} \tag*{$(3.2-16)$}
\end{equation}
ただし要素番号 $n$ の表示は省略しました。これをそれぞれ足しこんで全体の係数行列 $K^\ast$、$K^0$ とベクトル $F$ を作成すると次の方程式となります。
\begin{equation}
\sum_JK^\ast_{IJ}{\Delta A}_J=F_I+M_I-\sum_JK^0_{IJ}A_J \tag*{$(3.2-17)$}
\end{equation}
ここに $A_I$、$\Delta A_I$ は辺番号 $I$ の辺に対応するベクトルポテンシャル $\boldsymbol{A}$ とその増分 $\Delta\boldsymbol{A}$ の値です。
まず初期値としてすべての辺に対してベクトルポテンシャル値を決めます。通常はゼロとします。そうすると最初に解くべき方程式は、
\begin{equation}
\sum_JK^\ast_{IJ}{\Delta A}_J=F_I+M_I \notag
\end{equation}
となります。これを解いて $\Delta A$ が求まると最初のベクトルポテンシャルにこれを加えます。最初はベクトルポテンシャルをゼロとしていましたので、
\begin{equation}
A=0+\Delta A \notag
\end{equation}
です。これを(3.2-17)式の右辺に代入してこの方程式を解き求まった $\Delta A$ を先ほどのベクトルポテンシャルに加えて新しいベクトルポテンシャル $A_{new}$ を求めます。
\begin{equation}
A_{new}=A+\Delta A \tag*{$(3.2-18)$}
\end{equation}
これを(3.2-17)式の右辺に代入してこの方程式を解いて新たに求まった $\Delta A$ で次のベクトルポテンシャルを上の式で求めます。
これを繰り返して行き $\Delta A$ が十分小さくなったところで終了します。
あらかじめこの小さな値 $\epsilon$ を決めておき、
\begin{equation}
\frac{||\Delta A||}{||A||}<\epsilon \tag*{$(3.2-19)$}
\end{equation}
で判断します。ここに $||A||$ はベクトル $A$ のノルムで、
\begin{equation}
||A||=\sqrt{\frac{\sum_{I=1}^N{A_I}^2}{N}} \notag
\end{equation}
です。
特別な場合として線形磁性体の場合どうなるか見てみます。この場合、
\begin{equation}
\frac{\partial H_i}{\partial B_j}=\frac{1}{\mu}\delta_{ij} \notag
\end{equation}
なので(3.2-16)式の $K^\ast_{\alpha\beta}$ は(2.6-2)式の $K^{(n)}_{\alpha\beta}$ と一致します。
したがって、(3.2-17)式は次のようになります、
\begin{equation}
\sum_JK_{IJ}{\Delta A}_J=F_I+M_I-\sum_JK^0_{IJ}A_J \notag
\end{equation}
初期値としてベクトルポテンシャルをゼロとしている場合は磁束密度も磁荷もゼロとなるので、右辺第2項3項はゼロとなります。
\begin{equation}
\sum_JK_{IJ}{\Delta A}_J=F_I \notag
\end{equation}
これより次のベクトルポテンシャルはこの方程式をみたすので右辺は次のようになります。
\begin{equation}
F_I+M_I-\sum_JK^0_{IJ}A_J=\sum_JK_{IJ}A_J+M-\sum_JK^0_{IJ}A_I
=M-\sum_J(K^0_{IJ}-K_{IJ})A_J \notag
\end{equation}
磁化は、
\begin{equation}
\boldsymbol{M}=\frac{1}{\mu_0}\boldsymbol{B}-\boldsymbol{H}=\bigl(\frac{1}{\mu_0}-\frac{1}{\mu}\bigr)\boldsymbol{B} \notag
\end{equation}
なのでこれはゼロとなります。
したがってニュートン・ラプソン法の方程式の右辺はゼロとなり、次のベクトルポテンシャルの修正量はゼロとなり1回の繰り返しで収束します。
もちろん一般の非線形磁性体の場合複数回の繰り返し計算をする必要があります。場合によっては収束するには非常に多くの繰り返しが必要になることや収束しない場合があります。ニュートン・ラプソン法では最初の出発点が非常に重要でこれを適切に選ばない場合収束しない場合があります。
関数形によって収束が良い場合と悪い場合がありますが、一般に単調減少や単調増加の場合は収束性は良いのですがこのときも途中で変曲点がある S 字型の場合は収束が悪くなる傾向にあります。
一般に B-H 曲線は下の図のように最初はゆっくり上がっていますが途中から急激に立ち上がりその後ゆっくりと増加しています。
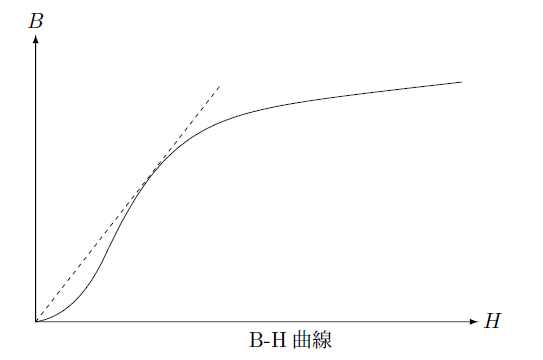
このような関数の場合ニュートン・ラプソン法の計算はなかなか収束しなくなります。
磁性体内部での磁場が大きい場合は小さなところでの磁化特性はあまり関係ないので図のように原点から B-H 曲線への接線を引き接点より小さなところでは、もとの曲線の代わりにこの直線を使うのも有効な方法です。
技術情報 Techinicalinfo
- ホーム
- 技術情報
- 【技術情報】有限要素法入門
- 3.2 非線形磁性体
【技術情報】有限要素法入門
