まず静電場について考えます。電場に関しては次の物質中のマックスウェルの方程式があります。
\begin{equation}
\mathrm{div}\boldsymbol{D}=\rho \tag*{$(1.1-1)$}
\end{equation}
ここに $\rho$ は電荷密度、$\boldsymbol{D}$ は電束密度です。
誘電率を $\epsilon$ とすれば電束密度は電場を使って次のように表されます。
\begin{equation}
\boldsymbol{D}=\epsilon\boldsymbol{E} \tag*{$(1.1-2)$}
\end{equation}
静電場はポテンシャル $\phi$ を使って次のように表すことができます。
\begin{equation}
\boldsymbol{E}=-\mathrm{grad}\phi \tag*{$(1.1-3)$}
\end{equation}
これは静電場が、
\begin{equation}
\mathrm{rot}\boldsymbol{E}=0 \tag*{$(1.1-4)$}
\end{equation}
をみたすからです。
ポテンシャルを使うと静電場の基礎方程式は次のようになります。
\begin{equation}
\mathrm{div}(\epsilon\mathrm{grad}\phi)=-\rho \tag*{$(1.1-5)$}
\end{equation}
この方程式は座標成分ごとに分けて次のようにかくことが出来ます。
\begin{equation}
\frac{\partial}{\partial x}\bigl(\epsilon\frac{\partial\phi}{\partial x}\bigr)+\frac{\partial}{\partial y}\bigl(\epsilon\frac{\partial\phi}{\partial y}\bigr)
+\frac{\partial}{\partial z}\bigl(\epsilon\frac{\partial\phi}{\partial z}\bigr)=-\rho \tag*{$(1.1-6)$}
\end{equation}
解析領域に複数の物質が存在する場合、誘電率は場所ごとに変化します。また右辺の電荷密度も一般的には場所の関数なのでこの方程式を直接解くのは難しいと思われます。
そこで問題をもう少し簡単にして、どのように方程式を解けばよいかを考えます。
まず誘電率や電荷密度が $x$ 方向にだけ変化し、 $y$ 、 $z$ 方向には変化しない場合、この方程式は次のように１次元の方程式となります。
\begin{equation}
\frac{d}{dx}\bigl(\epsilon\frac{d\phi}{dx}\bigr)=-\rho \tag*{$(1.1-7)$}
\end{equation}
微分は $x$ 方向の微分しか含んでないので常微分方程式です。ここで電荷密度が $x$ によらず一定の場合にはこの式の両辺は積分することができて、
\begin{equation}
\epsilon\frac{d\phi}{dx}=-\rho x + c \tag*{$(1.1-8)$}
\end{equation}
となります。ここで $c$ は積分定数でこの方程式を解くときの境界条件によって決まります。
解析領域として $x$ 軸上の区間 $[0,1]$ を考えます。$y$ 方向や $z$ 方向には変化しないので解析領域も１次元領域となります。
この端部の条件として、
\begin{equation}
\begin{split}
&D_x=0 \hspace{10mm} (x=0) \\
&\phi=0 \hspace{14mm} (x=1)
\end{split} \tag*{$(1.1-9)$}
\end{equation}
とすれば、最初の条件から、
\begin{equation}
D_x=-\epsilon\frac{d\phi}{dx}=\rho\times 0-c=0 \notag
\end{equation}
より積分定数 $c$ はゼロとなります。これから(１．１－８)式は、
\begin{equation}
\epsilon\frac{d\phi}{dx}=-\rho x \notag
\end{equation}
となりますが、この両辺を $x$ で積分して少し変形すると次のようになります。
\begin{equation}
\phi=-\frac{1}{2}\frac{\rho}{\epsilon}x^2+c^\prime \notag
\end{equation}
ここに $c^\prime$ は積分定数で(１．１－９)式の２番目の条件で決まります。この条件より、
\begin{equation}
0=-\frac{1}{2}\frac{\rho}{\epsilon}1^2+c^\prime \notag
\end{equation}
から、
\begin{equation}
c^\prime=\frac{1}{2}\frac{\rho}{\epsilon} \notag
\end{equation}
となり、ポテンシャルは次のように求まります。
\begin{equation}
\phi=\frac{1}{2}\frac{\rho}{\epsilon}(1-x^2) \tag*{$(1.1-10)$}
\end{equation}
このポテンシャルは方程式(１．１－７)式をみたし端部の条件(１．１－９)式、すなわち境界条件をみたしていることが分かります。
この例では誘電率と電荷密度が場所によって変化しないという条件のもとに解いたので比較的簡単に解けました。ところが一般的には複数の誘電体が解析領域に存在したり電荷密度が場所によって変化しますのでこのように簡単に解けるとは限りません。
そこで、１次元の方程式(１．１－７)式を $x$ 軸上の区間 $[a,b]$ において数値的に解くことを考えます。端部の境界条件は与えられているものとします。
数値的に解く場合この区間 $[a,b]$ を図のように幅 $\Delta x$ の小区間に分割し、ポテンシャルはその分割点でのみ値を持っているとして有限の値を未知数とした方程式を作ります。
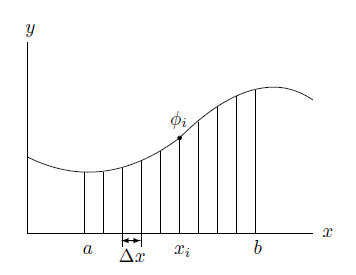
このように関数の値を有限の $x_i$ 座標に対応する値 $\phi_i$ とした場合、関数の微分は次のように近似できます。
\begin{equation}
\frac{d}{dx}\phi(x_i)=\frac{\phi_{i+1}-\phi_i}{\Delta x} \tag*{$(1.1-11)$}
\end{equation}
これを使うと(１．１－７)式の左辺は次のようにかけます。
\begin{equation}
\frac{1}{\Delta x}\bigl(\epsilon_i\frac{\phi_{i+1}-\phi_i}{\Delta x}-\epsilon_{i-1}\frac{\phi_i-\phi_{i-1}}{\Delta x}\bigr) \notag
\end{equation}
ただし誘電率はここでは点ごとに異なっているとして微分をとる区間の座標の小さなときの値を使っています。
これを(１．１－７)式に入れて $\phi_i$ に関する連立方程式を作り、その解をポテンシャルの値として計算する方法が差分法です。
ここではこれ以上差分法については述べませんが感じはつかんでいただけると思います。