ガウスの定理では面積分と体積積分が等しいという関係でしたが、この定理は2次元の場合でも同じように成り立ちます。
\begin{equation}
\oint\boldsymbol{v}\cdot\boldsymbol{n}dl=\int_S\bigl(\frac{\partial v_x}{\partial x}+\frac{\partial v_y}{\partial y}\bigr)dxdy \tag*{$(4-1)$}
\end{equation}
左辺の積分は面領域 $S$ の境界を一周する周回積分で、ベクトル場 $\boldsymbol{v}$ の法線成分を積分しています。それでは、次のように境界面の接線成分を積分すればどうなるでしょうか。
\begin{equation}
\oint\boldsymbol{v}\cdot\boldsymbol{t}dl \notag
\end{equation}
ここでベクトル $\boldsymbol{t}$ は積分する境界線にそった単位ベクトルです。
電磁気学の基本的な法則にアンペールの法則があります。これは電流があればその周りに電流を取り囲むように回転する磁場 $\boldsymbol{H}$ が発生するという法則で、式でかくと次のようになります。
\begin{equation}
\oint_C\boldsymbol{H}\cdot\boldsymbol{t}dl=i \tag*{$(4-2)$}
\end{equation}
ここで左辺の積分は電流 $i$ が流れている領域を取り囲む線 $C$ での周回積分でちょうど上で出てきた接線成分の積分となっています。
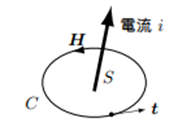
電流と言えば電線を流れる線状のものというイメージが強いですが、ここでは導体内部を分布して流れるものを想定しています。そうしますと導体内部では電流は水の流れのように場所によって異なる方向と大きさを持つベクトル場として考えることができます。水の場合流速を $\boldsymbol{v}$ とすれば、単位時間あたり単位面積を通過する流量は密度を $\rho$ とすれば $\rho|\boldsymbol{v}|$ となりますが方向も含めてベクトルとして $\rho\boldsymbol{v}$ として表すことができます。電流の場合も単位面積を単位時間に通過する電流を電流密度 $\boldsymbol{J}$ で表します。そうすれば水の流速ベクトルを面で積分したものがその面を通過して流れる水の量を表しているように、その面を通過して単位時間に流れる電荷の量すなわち電流を表すことができます。
\begin{equation}
i=\int_S\boldsymbol{J}\cdot\boldsymbol{n}dS \tag*{$(4-3)$}
\end{equation}
この式を使うと(4-2)式は次のようにかけます。
\begin{equation}
\oint_C\boldsymbol{H}\cdot\boldsymbol{t}dl=\int_S\boldsymbol{J}\cdot\boldsymbol{n}dS \tag*{$(4-4)$}
\end{equation}
この式の右辺の面積分を行う面 $S$ は平面である必要はありません。境界線を固定していればこの境界線を通過する電流はどのような面でとっても同じです。
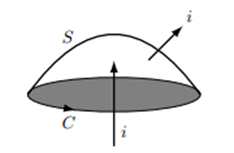
図のように下から入った電流 $i$ は上の曲面 $S$ を通して出ていきます。入ってくる電流と出ていく電流は等しいので積分面によらないことが分かります。アンペールの法則(4-4)式の左辺の線積分は積分路 $C$ によって決まるのは明らかですが、右辺の面積分もこの境界線だけで決まってしまうことになります。
ここからはこの法則に出てくるような線積分について考えていきます。ベクトル場としては磁場でも良いのですが、もう少しなじみのある水の速度場を考えます。
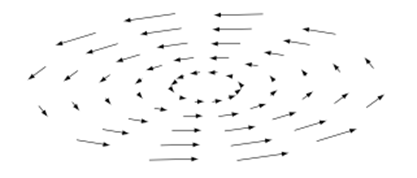
水が原点を中心に渦を作って回転している場合は、原点を取り囲む線で速度の接線成分を積分すると次のようになります。
\begin{equation}
\Omega=\oint_C\boldsymbol{v}\cdot\boldsymbol{t}dl \tag*{$(4-5)$}
\end{equation}
ここで $\Omega$ は渦を定量的に表す量と考えられます。実際、水が静止している場合や一定方向に同じ速度で流れているときはこの値はゼロとなり、回転速度が大きいほど大きくなります。回転には右回りと左回りという方向がありますが、この違いは $\Omega$ の符号で表すことができます。すなわち積分路の接線ベクトル $\boldsymbol{t}$ の取り方は二通りあるので、例えば原点を通る $z$ 軸方向に対して左回りの方向にとれば、左回りの渦の場合は正、右回りの場合は負となります。
(4-5)式は面 $S$ を取り囲む境界線 $C$ での周回積分ですが、ここで次の図にあるように面 $S_1$ と面 $S_2$ に分割することを考えます。
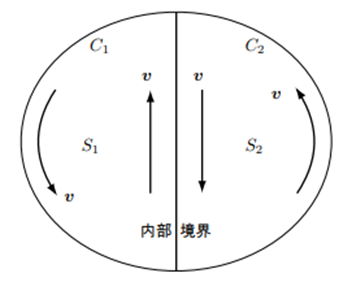
まず領域を二つに分割すればそれぞれの領域で、
\begin{equation}
\begin{split}
&\Omega_1=\oint_{C_1}\boldsymbol{v}\cdot\boldsymbol{t}dl \\
&\Omega_2=\oint_{C_2}\boldsymbol{v}\cdot\boldsymbol{t}dl
\end{split} \tag*{$(4-6)$}
\end{equation}
が定義できます。ここで線積分 $C_1$ $C_2$ は面領域 $S_1$ $S_2$ を取り囲む境界線です。したがって(4-5)式の積分路 $C$ には含まれていない内部境界線が含まれています。ところがこの内部境界線による積分は二つの領域では線積分の方向が逆になるので足し合わせた場合キャンセルして消えてしまいます。
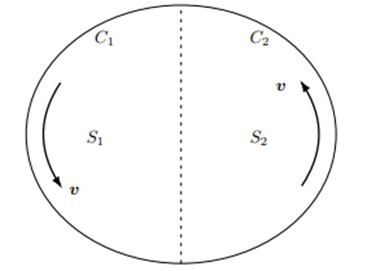
これより二つの領域の速度の線積分の和は領域境界だけの線積分となります。
\begin{equation}
\oint_{C_1}\boldsymbol{v}\cdot\boldsymbol{t}dl+\oint_{C_2}\boldsymbol{v}\cdot\boldsymbol{t}dl=\oint_C\boldsymbol{v}\cdot\boldsymbol{t}dl \tag*{$(4-7)$}
\end{equation}
すなわち、
\begin{equation}
\Omega=\Omega_1+\Omega_2 \tag*{$(4-8)$}
\end{equation}
となります。
このことはもっと多くの領域に分割した場合にも成り立ちます。例えば分割された $n$ 番目の領域 $S_n$ について、
\begin{equation}
\Omega_n=\oint_{C_n}\boldsymbol{v}\cdot\boldsymbol{t}dl \tag*{$(4-9)$}
\end{equation}
が定義できますがこれらを元の領域 $S$ になるように足し合わせるとどうなるかを考えます。
\begin{equation}
\sum_n\Omega_n=\sum_n\oint_{C_n}\boldsymbol{v}\cdot\boldsymbol{t}dl \tag*{$(4-10)$}
\end{equation}
この式の線積分は内部境界の寄与が図のように打ち消されますので最初の領域の境界上の積分だけが残ります。
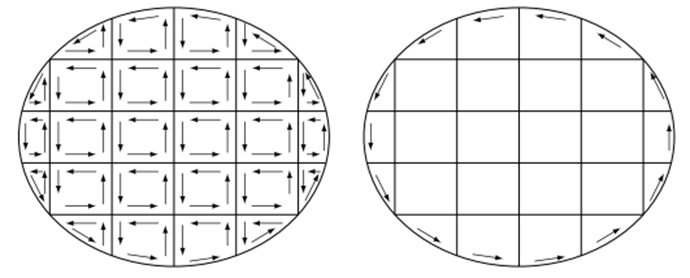
したがって、(4-10)式の右辺は次のように変形できます。
\begin{equation}
\sum_n\oint_{C_n}\boldsymbol{v}\cdot\boldsymbol{t}dl=\oint_C\boldsymbol{v}\cdot\boldsymbol{t}dl \tag*{$(4-11)$}
\end{equation}
これより次のようになります。
\begin{equation}
\Omega=\sum_n\Omega_n \tag*{$(4-12)$}
\end{equation}
このようにある面領域を取り囲む周回積分は、この面を分割して多くの面ごとの周回積分に分割してもそれを足し合わせると同じになります。ここでの説明で使った図では面領域 $S$ を平面として扱ってきましたが、どのような曲面に対しても成り立ちます。
アンペールの法則では磁場に関する周回積分が電流密度の面積分であるというように表現されていました。したがってこの回転を表す $\Omega$ を面積分で表現することを考えます。そのために、この面領域を小さな長方形で分割します。分割される面は一般には曲面ですが小さな面に分割するとこれらの面は平面に近づき、大きさをゼロにもっていく極限では完全に平面とみなすことができます。これらの面は方向は特別な座標系をとらない限り座標面と一致しているとは限りませんが、ここでは $xy$ 面に乗っているとして議論します。その結果は他の方向を持った平面に変換できますので最終的には曲面に関する関係が得られます。
まず、(4-9)式のように分割された長方形の一つを $x$ 方向の区間 $[a,a+\Delta x]$、$y$ 方向の区間 $[b,b+\Delta y]$ で囲まれる領域とすると線積分は四つの線に分割することができます。
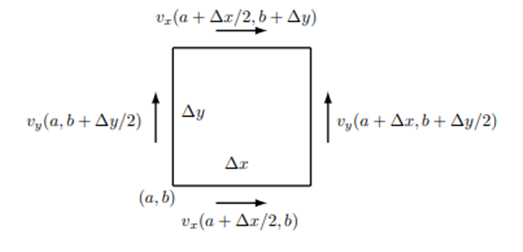
まず、線 $x=a$ では積分方向の単位ベクトル $(0,-1)$ とこの線の中心におけるベクトル $\boldsymbol{v}(a,b+\Delta y/2)$ から積分は次のようになります。
\begin{equation}
-v_y\bigl(a,b+\frac{\Delta y}{2}\bigr)\Delta y \notag
\end{equation}
次に、線 $x=a+\Delta x$ では積分方向の単位ベクトル $(0,1)$ とこの線の中心におけるベクトル $\boldsymbol{v}(a+\Delta x,b+\Delta y/2)$ から積分は次のようになります。
\begin{equation}
v_y\bigl(a+\Delta x,b+\frac{\Delta y}{2}\bigr)\Delta y \notag
\end{equation}
したがって、両者の和は
\begin{equation}
\begin{split}
&\bigl[v_y\bigl(a+\Delta x,b+\frac{\Delta y}{2}\bigr)-v_y\bigl(a,b+\frac{\Delta y}{2}\bigr)\bigr]\Delta y \\
&=\frac{v_y\bigl(a+\Delta x,b+\frac{\Delta y}{2}\bigr)-v_y\bigl(a,b+\frac{\Delta y}{2}\bigr)}{\Delta x}\Delta x\Delta y
\end{split} \notag
\end{equation}
となります。この式の右辺は区間 $\Delta x$ をゼロに近づけた極限において変数 $x$ による偏微分となるので、次のようにかくことができます。
\begin{equation}
\frac{\partial v_y}{\partial x}\Delta x\Delta y \notag
\end{equation}
同様にして線 $y=b$ と線 $y+\Delta y$ についての積分は、
\begin{equation}
-\frac{\partial v_x}{\partial y}\Delta x\Delta y \notag
\end{equation}
となるので、結局(4-9)式は次のようになります。
\begin{equation}
\oint_{C_n}\boldsymbol{v}\cdot\boldsymbol{t}dl=\bigl(\frac{\partial v_y}{\partial x}-\frac{\partial v_x}{\partial y}\bigr)\Delta x\Delta y \tag*{$(4-13)$}
\end{equation}
したがって、(4-10)式はこの右辺の和として次のように表すことができます。
\begin{equation}
\sum_n\oint_{C_n}\boldsymbol{v}\cdot\boldsymbol{t}dl=\sum_n\bigl(\frac{\partial v_y}{\partial x}-\frac{\partial v_x}{\partial y}\bigr)\Delta x\Delta y \tag*{$(4-14)$}
\end{equation}
ここで右辺の和は領域に含まれる微小な長方形すべてについてとり、微分はこれらの直方体の中心における値です。この長方形の大きさをゼロに近づけた極限において面積分になります。
\begin{equation}
\oint_C\boldsymbol{v}\cdot\boldsymbol{t}dl=\int_S\bigl(\frac{\partial v_y}{\partial x}-\frac{\partial v_x}{\partial y}\bigr)dxdy \tag*{$(4-15)$}
\end{equation}
この式の左辺は線積分であり右辺は面積分となっており、当初の面積分で表すという目的が達成できました。ただしここでの分割された微小面領域は $xy$ 面であるとしていたのでこのままでは分割される前の領域も $xy$ 面に限定されたものになってしまいます。
他の座標面でも上に述べたのと同様な方法が使えます。
$yz$ 面では、
\begin{equation}
\oint_{C_{yz}}\boldsymbol{v}\cdot\boldsymbol{t}dl=\int_S\bigl(\frac{\partial v_z}{\partial y}-\frac{\partial v_y}{\partial z}\bigr)dydz \tag*{$(4-16)$}
\end{equation}
$zx$ 面では、
\begin{equation}
\oint_{C_{zx}}\boldsymbol{v}\cdot\boldsymbol{t}dl=\int_S\bigl(\frac{\partial v_x}{\partial z}-\frac{\partial v_z}{\partial x}\bigr)dzdx \tag*{$(4-17)$}
\end{equation}
となります。
それでは座標面に乗っていない面に対してはどうなるでしょうか。
そこで下の図のように点 $a$、$b$、$c$ で作られる三角形の面を考えます。
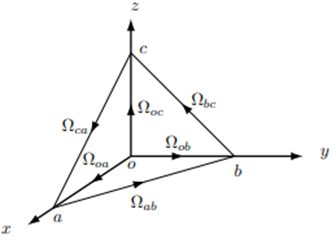
この面における積分は次のようになります。
\begin{equation}
\Omega_{abc}=\int_a^b\boldsymbol{v}\cdot\boldsymbol{t}dl+\int_b^c\boldsymbol{v}\cdot\boldsymbol{t}dl+\int_c^a\boldsymbol{v}\cdot\boldsymbol{t}dl \tag*{$(4-18)$}
\end{equation}
この右辺の積分をそれぞれ次のように定義します。
\begin{equation}
\Omega_{ab}\equiv\int_a^b\boldsymbol{v}\cdot\boldsymbol{t}dl \hspace{10mm}
\Omega_{bc}\equiv\int_b^c\boldsymbol{v}\cdot\boldsymbol{t}dl \hspace{10mm}
\Omega_{ca}\equiv\int_c^a\boldsymbol{v}\cdot\boldsymbol{t}dl \tag*{$(4-19)$}
\end{equation}
また座標軸に沿った積分を、
\begin{equation}
\Omega_{oa}\equiv\int_o^a\boldsymbol{v}\cdot\boldsymbol{t}dl \hspace{10mm}
\Omega_{ob}\equiv\int_o^b\boldsymbol{v}\cdot\boldsymbol{t}dl \hspace{10mm}
\Omega_{oc}\equiv\int_o^c\boldsymbol{v}\cdot\boldsymbol{t}dl \tag*{$(4-20)$}
\end{equation}
とします。これを使うと(4-18)式は次のようにかけます。
\begin{equation}
\Omega{abc}=\Omega_{ab}+\Omega_{bc}+\Omega_{ca} \tag*{$(4-21)$}
\end{equation}
また座標面に乗っている三角形$\Delta_{oab}$、$\Delta_{obc}$、$\Delta_{oca}$に対しては、
\begin{equation}
\begin{split}
&\Omega{oab}=\Omega_{oa}+\Omega_{ab}+\Omega_{bo} \\
&\Omega{obc}=\Omega_{ob}+\Omega_{bc}+\Omega_{co} \\
&\Omega{oca}=\Omega_{oc}+\Omega_{ca}+\Omega_{ao}
\end{split} \tag*{$(4-22)$}
\end{equation}
となります。ここで、$\Omega_{ao}=-\Omega_{oa}$ などに注意すれば次のようになります。
\begin{equation}
\begin{split}
\Omega_{oab}+\Omega_{obc}+\Omega_{oca}&=\Omega_{oa}+\Omega_{ab}+\Omega_{bo} \\
&+\Omega_{ob}+\Omega_{bc}+\Omega_{co} \\
&+\Omega_{oc}+\Omega_{ca}+\Omega_{ao} \\
&=\Omega_{ab}+\Omega_{bc}+\Omega_{ca}
\end{split} \notag
\end{equation}
この右辺は(4-21)に一致するので次の関係が成立します。
\begin{equation}
\Omega_{abc}=\Omega_{oab}+\Omega_{obc}+\Omega_{oca} \tag*{$(4-23)$}
\end{equation}
これで三角面 $abc$ での積分 $\Omega_{abc}$ を、座標面に乗った三角形における積分の和で表すことができました。(4-15)、(4-16)、(4-17)式を使うと、
\begin{equation}
\begin{split}
\Omega_{abc}&=\int_S\bigl(\frac{\partial v_y}{\partial x}-\frac{\partial v_x}{\partial y}\bigr)dxdy \\
&+\int_S\bigl(\frac{\partial v_z}{\partial y}-\frac{\partial v_y}{\partial z}\bigr)dydz \\
&+\int_S\bigl(\frac{\partial v_x}{\partial z}-\frac{\partial v_z}{\partial x}\bigr)dzdx
\end{split} \tag*{$(4-24)$}
\end{equation}
となります。ここで考えている領域の大きさは非常に小さいと考えているので面積分は積分されるものと面積の積としてもよいので、
\begin{equation}
\begin{split}
\Omega_{abc}&=\bigl(\frac{\partial v_y}{\partial x}-\frac{\partial v_x}{\partial y}\bigr)\Delta S_{xy} \\
&+\bigl(\frac{\partial v_z}{\partial y}-\frac{\partial v_y}{\partial z}\bigr)\Delta S_{yz} \\
&+\bigl(\frac{\partial v_x}{\partial z}-\frac{\partial v_z}{\partial x}\bigr)\Delta S_{zx}
\end{split} \tag*{$(4-25)$}
\end{equation}
となります。ここに $\Delta S_{xy}$ は三角形 $\Delta_{xy}$ の面積などです。
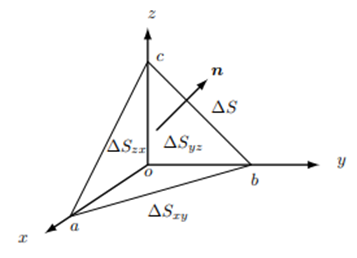
図のように今考えている三角形 $\Delta_{abc}$ の面積を $\Delta S$、単位法線ベクトルを $\boldsymbol{n}$ とすれば、これらの座標面の三角形の面積はこの三角形の射影成分ですから法線ベクトルの成分を使って次のようになります。
\begin{equation}
\begin{split}
&\Delta S_{xy}=n_z\Delta S \\
&\Delta S_{yz}=n_x\Delta S \\
&\Delta S_{zx}=n_y\Delta S
\end{split} \tag*{$(4-26)$}
\end{equation}
この関係が成り立つのは次のように考えれば分かりやすいでしょう。この図の下から上、つまり $z$ 方向に一様な水の流れがあるとします。この場合底面 $\Delta S_{xy}$ から水が入ってきます。水の速さを $v$ とすれば、この四面体に単位時間に入ってくる水の量は $v\Delta S_{xy}$ となります。一方水は $\Delta S$ の面から出ていきますがその量は $\boldsymbol{v}\cdot\boldsymbol{n}\Delta S=vn_z\Delta S$ となります。水の速度成分は $z$ 方向のみだからです。これより、$\Delta S_{xy}=n_z\Delta $ となります。
これを使うと(4-25)式の右辺は次のようになります。
\begin{equation}
\bigl(\frac{\partial v_y}{\partial x}-\frac{\partial v_x}{\partial y}\bigr)n_z\Delta S
+\bigl(\frac{\partial v_z}{\partial y}-\frac{\partial v_y}{\partial z}\bigr)n_x\Delta S
+\bigl(\frac{\partial v_x}{\partial z}-\frac{\partial v_z}{\partial x}\bigr)n_y\Delta S \notag
\end{equation}
ここで次のような成分を持つベクトルを考えます。
\begin{equation}
\boldsymbol{\omega}=\bigl(\frac{\partial v_z}{\partial y}-\frac{\partial v_y}{\partial z},
\frac{\partial v_x}{\partial z}-\frac{\partial v_z}{\partial x},
\frac{\partial v_y}{\partial x}-\frac{\partial v_x}{\partial y}\bigr) \tag*{$(4-27)$}
\end{equation}
このベクトルの成分は上の式にあらわれる項と同じものですが、この順番でベクトルの成分であることを示すことができます。これより(4-25)式は次のようにかくことができます。
\begin{equation}
\Omega_{abc}=(\omega_zn_z+\omega_xn_x+\omega_yn_y)\Delta S=\boldsymbol{\omega}\cdot\boldsymbol{n}\Delta S \tag*{$(4-28)$}
\end{equation}
これを使うと(4-15)式を一般の曲面に拡張して次のようにかくことができます。
\begin{equation}
\oint_C\boldsymbol{v}\cdot\boldsymbol{t}dl=\int_S\boldsymbol{\omega}\cdot\boldsymbol{n}dS \tag*{$(4-29)$}
\end{equation}
このようにベクトル $\boldsymbol{\omega}$ はベクトル $\boldsymbol{v}$ の回転を表したベクトルなので、回転を表す演算を、
\begin{equation}
\mathrm{rot}\boldsymbol{v}=\bigl(\frac{\partial v_z}{\partial y}-\frac{\partial v_y}{\partial z},
\frac{\partial v_x}{\partial z}-\frac{\partial v_z}{\partial x},
\frac{\partial v_y}{\partial x}-\frac{\partial v_x}{\partial y}\bigr) \tag*{$(4-30)$}
\end{equation}
と定義します。これを使うと(4-29)式は、両辺を入れ替えて次のようになります。
\begin{equation}
\int_S\mathrm{rot}\boldsymbol{v}\cdot\boldsymbol{n}dS=\oint_C\boldsymbol{v}\cdot\boldsymbol{t}dl \tag*{$(4-31)$}
\end{equation}
左辺のベクトルの回転についての面積分がその面の境界線上での周回積分と等しくなるという関係ですが、これをストークスの定理と呼んでいます。これより(4-4)式で表されるアンペールの法則は次のようになります。
\begin{equation}
\int_S\mathrm{rot}\boldsymbol{H}\cdot\boldsymbol{n}dS=\int_S\boldsymbol{J}\cdot\boldsymbol{n}dS \tag*{$(4-32)$}
\end{equation}
この積分領域 $S$ はどのようにでもとれますので結局次の方程式となります。
\begin{equation}
\mathrm{rot}\boldsymbol{H}=\boldsymbol{J} \tag*{$(4-33)$}
\end{equation}
少し式が多くなったので回転する速度場の簡単な例を示しておきます。図のように中心軸周りを角速度 $\omega$ で回転する円盤を考えます。
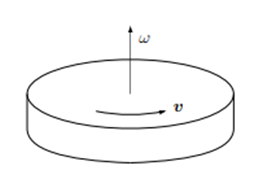
このとき円盤の速度 $\boldsymbol{v}$ は場所によって異なりますが、中心軸から距離 $r$ 離れた位置における速さは、
\begin{equation}
v=r\omega \notag
\end{equation}
となります。速度は周方向を向いているのでこの点の座標を $(x,y)$ とすれば速度の成分は次のようになります。
\begin{equation}
\begin{split}
&v_x=-\omega y \\
&v_y=\omega x \\
&v_z=0
\end{split} \notag
\end{equation}
これより(4-30)式を計算すると、
\begin{equation}
\begin{split}
&(\mathrm{rot}\boldsymbol{v})_x=\frac{\partial v_z}{\partial y}-\frac{\partial v_y}{\partial z}=0 \\
&(\mathrm{rot}\boldsymbol{v})_y=\frac{\partial v_x}{\partial z}-\frac{\partial v_z}{\partial x}=0 \\
&(\mathrm{rot}\boldsymbol{v})_z=\frac{\partial v_y}{\partial x}-\frac{\partial v_x}{\partial y}=2\omega
\end{split} \notag
\end{equation}
となります。このベクトルの方向は回転軸方向を向いており、大きさは角速度の2倍であり場所によらず一定となっています。もちろんこの例は円盤の回転という特殊な例ですが、回転の演算子である $\mathrm{rot}$ が速度場の回転を表していることを感じていただけると思います。この場合のストークスの定理ですが、(4-31)式の左辺の面積分は $\mathrm{rot}\boldsymbol{v}$ が一定であり法線ベクトルも常に $z$ 方向を向いているので、この積分面を半径 $R$ の円の内部とすれば、$2\omega$ にこの面積をかけたものになるので、
\begin{equation}
\int_S\mathrm{rot}\boldsymbol{v}\cdot\boldsymbol{n}dS=2\omega\times\pi R^2=4\pi R^2\omega \notag
\end{equation}
です。一方右辺は半径 $R$ の位置にある速さ $R\omega$ にこの円の周長をかけたものですから次のようになります。
\begin{equation}
\oint_C\boldsymbol{v}\cdot\boldsymbol{t}dl=2\pi R\times R\omega=4\pi R^2\omega \notag
\end{equation}
確かに両者が等しくなることが確認できました。
