今までは要素の節点にスカラーやベクトルの値を持たせて要素内の値を補間してきました。このような要素を節点要素とよんでいます。
これに対して要素を構成する辺に値を持たせることがあります。辺は方向を持っていますので辺の値によって大きさと方向を持たせたベクトルを表現するのです。つまりベクトルの辺への射影成分を持たせこれによって要素内のベクトルを補間します。
このような要素のことを辺要素とよんでいます。
磁場解析の場合3次元ではこの辺要素の使用が主流になってきています。
まず、このように辺に値を持たせるという考え方がどのようなものなのかを六面体のアイソパラメトリック要素を例にとり説明します。
節点要素の場合補間関数を標準座標で表すと(1.4-10)式、
\begin{equation}
\begin{split}
&N_1(r,s,t)=\frac{1}{8}(1-r)(1-s)(1-t) \hspace{10mm} N_2(r,s,t)=\frac{1}{8}(1+r)(1-s)(1-t) \\
&N_3(r,s,t)=\frac{1}{8}(1+r)(1+s)(1-t) \hspace{10mm} N_4(r,s,t)=\frac{1}{8}(1-r)(1+s)(1-t) \\
&N_5(r,s,t)=\frac{1}{8}(1-r)(1-s)(1+t) \hspace{10mm} N_6(r,s,t)=\frac{1}{8}(1+r)(1-s)(1+t) \\
&N_7(r,s,t)=\frac{1}{8}(1+r)(1+s)(1+t) \hspace{10mm} N_8(r,s,t)=\frac{1}{8}(1-r)(1+s)(1+t)
\end{split} \notag
\end{equation}
です。これを使って要素内のスカラー場 $\phi$ を表すと次のようになります。
\begin{equation}
\phi(x,y,z)=\sum_{\alpha=1}^8N_\alpha(r,s,t)\phi^\alpha \tag*{$(2.5-1)$}
\end{equation}
このスカラー場の勾配は、
\begin{equation}
\frac{\partial\phi}{\partial x_i}=\sum_{\alpha=1}^8\frac{\partial N_\alpha}{\partial x_i}\phi^\alpha
=\sum_{\alpha=1}^8\frac{\partial N_\alpha}{\partial r}\frac{\partial r}{\partial x_i}\phi^\alpha
+\sum_{\alpha=1}^8\frac{\partial N_\alpha}{\partial s}\frac{\partial s}{\partial x_i}\phi^\alpha
+\sum_{\alpha=1}^8\frac{\partial N_\alpha}{\partial t}\frac{\partial t}{\partial x_i}\phi^\alpha \tag*{$(2.5-2)$}
\end{equation}
となります。右辺の各項を計算すると、
\begin{equation}
\begin{split}
\sum_{\alpha=1}^8\frac{\partial N_\alpha}{\partial r}\frac{\partial r}{\partial x_i}\phi^\alpha
&=\frac{1}{4}(1-s)(1-t)\frac{\partial r}{\partial x_i}\frac{\phi^2-\phi^1}{2}
+\frac{1}{4}(1+s)(1-t)\frac{\partial r}{\partial x_i}\frac{\phi^3-\phi^4}{2} \\
&+\frac{1}{4}(1+s)(1+t)\frac{\partial r}{\partial x_i}\frac{\phi^7-\phi^8}{2}
+\frac{1}{4}(1-s)(1+t)\frac{\partial r}{\partial x_i}\frac{\phi^6-\phi^5}{2} \\
\sum_{\alpha=1}^8\frac{\partial N_\alpha}{\partial s}\frac{\partial s}{\partial x_i}\phi^\alpha
&=\frac{1}{4}(1-t)(1-r)\frac{\partial s}{\partial x_i}\frac{\phi^4-\phi^1}{2}
+\frac{1}{4}(1+t)(1-r)\frac{\partial s}{\partial x_i}\frac{\phi^8-\phi^5}{2} \\
&+\frac{1}{4}(1+t)(1+r)\frac{\phi^7-\phi^6}{2}+\frac{1}{4}(1-t)(1+r)\frac{\phi^3-\phi^2}{2} \\
\sum_{\alpha=1}^8\frac{\partial N_\alpha}{\partial t}\frac{\partial t}{\partial x_i}\phi^\alpha
&=\frac{1}{4}(1-r)(1-s)\frac{\partial t}{\partial x_i}\frac{\phi^5-\phi^1}{2}
+\frac{1}{4}(1+r)(1-s)\frac{\partial t}{\partial x_i}\frac{\phi^6-\phi^2}{2} \\
&+\frac{1}{4}(1+r)(1+s)\frac{\partial t}{\partial x_i}\frac{\phi^7-\phi^3}{2}
+\frac{1}{4}(1-r)(1+s)\frac{\partial t}{\partial x_i}\frac{\phi^8-\phi^4}{2} \\
\end{split} \notag
\end{equation}
となります。そこで、
\begin{equation}
\begin{split}
&(N_1)_i=\frac{1}{4}(1-s)(1-t)\frac{\partial r}{\partial x_i} \hspace{12mm} (N_2)_i=\frac{1}{4}(1+s)(1-t)\frac{\partial r}{\partial x_i} \\
&(N_3)_i=\frac{1}{4}(1+s)(1+t)\frac{\partial r}{\partial x_i} \hspace{12mm} (N_4)_i=\frac{1}{4}(1-s)(1+t)\frac{\partial r}{\partial x_i} \\
&(N_5)_i=\frac{1}{4}(1-t)(1-r)\frac{\partial s}{\partial x_i} \hspace{12mm} (N_6)_i=\frac{1}{4}(1+t)(1-r)\frac{\partial s}{\partial x_i} \\
&(N_7)_i=\frac{1}{4}(1+t)(1+r)\frac{\partial s}{\partial x_i} \hspace{12mm} (N_8)_i=\frac{1}{4}(1-t)(1+r)\frac{\partial s}{\partial x_i} \\
&(N_9)_i=\frac{1}{4}(1-r)(1-s)\frac{\partial t}{\partial x_i} \hspace{12mm} (N_{10})_i=\frac{1}{4}(1+r)(1-s)\frac{\partial t}{\partial x_i} \\
&(N_{11})_i=\frac{1}{4}(1+r)(1+s)\frac{\partial t}{\partial x_i} \hspace{11mm} (N_{12})_i=\frac{1}{4}(1-r)(1+s)\frac{\partial t}{\partial x_i}
\end{split} \tag*{$(2.5-3)$}
\end{equation}
\begin{equation}
\begin{split}
&\Delta\phi^1=\frac{\phi^2-\phi^1}{2} \hspace{5mm} \Delta\phi^2=\frac{\phi^3-\phi^4}{2} \hspace{5mm}
\Delta\phi^3=\frac{\phi^7-\phi^8}{2} \hspace{5mm} \Delta\phi^4=\frac{\phi^6-\phi^5}{2} \hspace{5mm} \\
&\Delta\phi^5=\frac{\phi^4-\phi^1}{2} \hspace{5mm} \Delta\phi^6=\frac{\phi^8-\phi^5}{2} \hspace{5mm}
\Delta\phi^7=\frac{\phi^7-\phi^6}{2} \hspace{5mm} \Delta\phi^8=\frac{\phi^3-\phi^2}{2} \hspace{5mm} \\
&\Delta\phi^9=\frac{\phi^5-\phi^1}{2} \hspace{5mm} \Delta\phi^{10}=\frac{\phi^6-\phi^2}{2} \hspace{4mm}
\Delta\phi^{11}=\frac{\phi^7-\phi^3}{2} \hspace{4mm} \Delta\phi^{12}=\frac{\phi^8-\phi^4}{2}
\end{split} \tag*{$(2.5-4)$}
\end{equation}
とおくと、ポテンシャルの勾配(2.5-2)式は次のようにかくことができます。
\begin{equation}
\frac{\partial\phi}{\partial x_i}=\sum_{\alpha=1}^{12}(N_\alpha)_i(r,s,t)\Delta\phi^\alpha \tag*{$(2.5-5)$}
\end{equation}
この式は要素内のスカラー関数 $\phi$ の勾配を、辺におけるこのポテンシャルの差$\Delta\phi^\alpha$で補間しているとみることができます。
また、この量は次のように表すことが出来ます。
\begin{equation}
\Delta\phi^\alpha=\frac{1}{2}\int_{p_1}^{p_2}\mathrm{grad}\phi\cdot d\boldsymbol{l} \tag*{$(2.5-6)$}
\end{equation}
ここに、辺の番号を $\alpha$ として辺の端点を $p_1$、$p_2$ としました。また $d\boldsymbol{l} $はこの辺の線素です。
これより、(2.5-5)式は要素内のスカラー場の勾配 $\mathrm{grad}\phi$ を辺上のこのベクトルの射影成分の積分で表現していることが分かります。したがって、要素内のベクトルを、辺上のベクトルの射影成分の積分で表していることになり、要素内の値を節点値で補間する節点要素に対応して辺の値で補間していることになります。
ところで(2.5-5)式の右辺は辺の数だけの和をとっていますが、(2.5-4)式で表される $\Delta\phi^\alpha$ は $\phi$ の節点値の数しかないのでこれらの量はすべて独立ではありません。これは $\mathrm{grad}\phi$ が一般のベクトルではなく勾配を表すベクトルだからです。
$\Delta\phi$ は $\phi$ の両端での値の差なので、一つの辺の端点から出発して辺に沿ってこの値を足して行くと、閉じたループで一周したときゼロとなります。
つまり、
\begin{equation}
\oint\mathrm{grad}\phi\cdot d\boldsymbol{l}=0 \notag
\end{equation}
です。この式は、
\begin{equation}
\mathrm{rot}\mathrm{grad}\phi=0 \notag
\end{equation}
に対応しています。
ここで(2.5-5)式を一般のベクトル場 $\boldsymbol{v}$ に拡張して次のようにかいてみます。
\begin{equation}
v_i=\sum_{\alpha=1}^{12}(N_\alpha)_i(r,s,t)v^\alpha \tag*{$(2.5-7)$}
\end{equation}
ここに、辺の端点を $p_1$、$p_2$ としたとき、
\begin{equation}
v^\alpha=\frac{1}{2}\int_{p_1}^{p_2}\boldsymbol{v}\cdot d\boldsymbol{l} \tag*{$(2.5-8)$}
\end{equation}
です。(2.5-7)式はベクトルでかいて次のように表すこともできます。
\begin{equation}
\boldsymbol{v}=\sum_{\alpha=1}^{12}\boldsymbol{N}_\alpha(r,s,t)v^\alpha \tag*{$(2.5-9)$}
\end{equation}
この式は、先ほどの勾配ベクトルの場合と違って辺の値 $v^\alpha$ はすべて独立にとれます。またこの場合の補間関数はベクトルとなっていますので、(2.5-3)式のことをベクトル補間関数とよんでいます。
辺要素では要素内のベクトルを辺上の値で補間できることが分かりました。このとき全ての辺は方向を持っておりその方向ベクトルとベクトルとの内積をとるのでこの方向をどのように決めるかで補間関数も変わります。ここで定義した補間関数と辺の方向を、節点番号と辺番号の関係と合わせて下の図に示します。
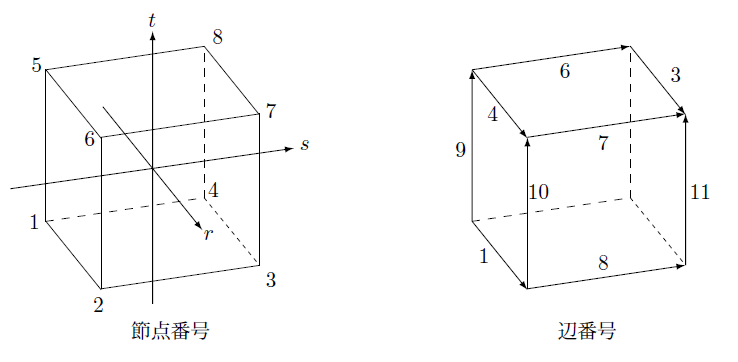
辺要素を有限要素法で扱う場合ベクトル場の空間微分をとる必要があります。
\begin{equation}
\frac{\partial\boldsymbol{v}}{\partial x_i}=\sum_{\alpha=1}^{12}\frac{\partial\boldsymbol{N}_\alpha}{\partial x_i}v^\alpha \tag*{$(2.5-10)$}
\end{equation}
ここで補間関数の微分を(2.5-3)式から計算しておきます。
\begin{equation}
\begin{split}
&\frac{\partial(N_1)_j}{\partial x_i}\hspace{2mm}=-\frac{1}{4}(1-t)\frac{\partial s}{\partial x_i}\frac{\partial r}{\partial x_j}
-\frac{1}{4}(1-s)\frac{\partial t}{\partial x_i}\frac{\partial r}{\partial x_j}+\frac{1}{4}(1-s)(1-t)\frac{\partial^2r}{\partial x_i\partial x_j} \\
&\frac{\partial(N_2)_j}{\partial x_i}\hspace{2mm}=+\frac{1}{4}(1-t)\frac{\partial s}{\partial x_i}\frac{\partial r}{\partial x_j}
-\frac{1}{4}(1+s)\frac{\partial t}{\partial x_i}\frac{\partial r}{\partial x_j}+\frac{1}{4}(1+s)(1-t)\frac{\partial^2r}{\partial x_i\partial x_j} \\
&\frac{\partial(N_3)_j}{\partial x_i}\hspace{2mm}=+\frac{1}{4}(1+t)\frac{\partial s}{\partial x_i}\frac{\partial r}{\partial x_j}
+\frac{1}{4}(1+s)\frac{\partial t}{\partial x_i}\frac{\partial r}{\partial x_j}+\frac{1}{4}(1+s)(1+t)\frac{\partial^2r}{\partial x_i\partial x_j} \\
&\frac{\partial(N_4)_j}{\partial x_i}\hspace{2mm}=-\frac{1}{4}(1+t)\frac{\partial s}{\partial x_i}\frac{\partial r}{\partial x_j}
+\frac{1}{4}(1-s)\frac{\partial t}{\partial x_i}\frac{\partial r}{\partial x_j}+\frac{1}{4}(1-s)(1+t)\frac{\partial^2r}{\partial x_i\partial x_j} \\
&\frac{\partial(N_5)_j}{\partial x_i}\hspace{2mm}=-\frac{1}{4}(1-r)\frac{\partial t}{\partial x_i}\frac{\partial s}{\partial x_j}
-\frac{1}{4}(1-t)\frac{\partial r}{\partial x_i}\frac{\partial s}{\partial x_j}+\frac{1}{4}(1-t)(1-r)\frac{\partial^2s}{\partial x_i\partial x_j} \\
&\frac{\partial(N_6)_j}{\partial x_i}\hspace{2mm}=+\frac{1}{4}(1-r)\frac{\partial t}{\partial x_i}\frac{\partial s}{\partial x_j}
-\frac{1}{4}(1+t)\frac{\partial r}{\partial x_i}\frac{\partial s}{\partial x_j}+\frac{1}{4}(1+t)(1-r)\frac{\partial^2s}{\partial x_i\partial x_j} \\
&\frac{\partial(N_7)_j}{\partial x_i}\hspace{2mm}=+\frac{1}{4}(1+r)\frac{\partial t}{\partial x_i}\frac{\partial s}{\partial x_j}
+\frac{1}{4}(1+t)\frac{\partial r}{\partial x_i}\frac{\partial s}{\partial x_j}+\frac{1}{4}(1+t)(1+r)\frac{\partial^2s}{\partial x_i\partial x_j} \\
&\frac{\partial(N_8)_j}{\partial x_i}\hspace{2mm}=-\frac{1}{4}(1+r)\frac{\partial t}{\partial x_i}\frac{\partial s}{\partial x_j}
+\frac{1}{4}(1-t)\frac{\partial r}{\partial x_i}\frac{\partial s}{\partial x_j}+\frac{1}{4}(1-t)(1+r)\frac{\partial^2s}{\partial x_i\partial x_j} \\
&\frac{\partial(N_9)_j}{\partial x_i}\hspace{2mm}=-\frac{1}{4}(1-s)\frac{\partial r}{\partial x_i}\frac{\partial t}{\partial x_j}
-\frac{1}{4}(1-r)\frac{\partial s}{\partial x_i}\frac{\partial t}{\partial x_j}+\frac{1}{4}(1-r)(1-s)\frac{\partial^2t}{\partial x_i\partial x_j} \\
&\frac{\partial(N_{10})_j}{\partial x_i}=+\frac{1}{4}(1-s)\frac{\partial r}{\partial x_i}\frac{\partial t}{\partial x_j}
-\frac{1}{4}(1+r)\frac{\partial s}{\partial x_i}\frac{\partial t}{\partial x_j}+\frac{1}{4}(1+r)(1-s)\frac{\partial^2t}{\partial x_i\partial x_j} \\
&\frac{\partial(N_{11})_j}{\partial x_i}=+\frac{1}{4}(1+s)\frac{\partial r}{\partial x_i}\frac{\partial t}{\partial x_j}
+\frac{1}{4}(1+r)\frac{\partial s}{\partial x_i}\frac{\partial t}{\partial x_j}+\frac{1}{4}(1+r)(1+s)\frac{\partial^2t}{\partial x_i\partial x_j} \\
&\frac{\partial(N_{12})_j}{\partial x_i}=-\frac{1}{4}(1+s)\frac{\partial r}{\partial x_i}\frac{\partial t}{\partial x_j}
+\frac{1}{4}(1-r)\frac{\partial s}{\partial x_i}\frac{\partial t}{\partial x_j}+\frac{1}{4}(1-r)(1+s)\frac{\partial^2t}{\partial x_i\partial x_j} \\
\end{split} \notag
\end{equation}
次に四面体要素の辺要素の補間関数を求めます。
節点要素の場合(1.4-7)式の補間関数を使って要素内のベクトルは、
\begin{equation}
\boldsymbol{v}=\sum_{\alpha=1}^4N_\alpha\boldsymbol{v}^\alpha \tag*{$(2.5-11)$}
\end{equation}
と節点値 $\boldsymbol{v}^\alpha$ を使って補間できます。ここで節点 $\alpha$ から $\beta$ に向かう辺ベクトルを、
\begin{equation}
\boldsymbol{x}^{\alpha\beta}=\boldsymbol{x}^\beta-\boldsymbol{x}^\alpha \notag
\end{equation}
と定義します。これを使うと辺要素で使う辺上の値として次の量を考えることが出来ます。
\begin{equation}
v^{\alpha\beta}=\boldsymbol{x}^{\alpha\beta}\cdot\boldsymbol{v} \tag*{$(2.5-12)$}
\end{equation}
四面体の辺要素では辺上のベクトルの射影成分は辺に沿って変化しないので、この式の右辺はベクトル $\boldsymbol{v}$ の射影成分を辺上で積分したものとなっています。
これより各節点におけるベクトル $\boldsymbol{v}^\alpha$ もこの関係をみたす必要があり次式が成り立ちます。
\begin{equation}
v^{\alpha\beta}=\boldsymbol{x}^{\alpha\beta}\cdot\boldsymbol{v}^\alpha \notag
\end{equation}
例えば節点$1$は他の三つの節点と辺で結ばれていますのでこの方程式は次のようにかけます。
\begin{equation}
\begin{bmatrix}
(x^{12})_x & (x^{12})_y & (x^{12})_z \\
(x^{13})_x & (x^{13})_y & (x^{13})_z \\
(x^{14})_x & (x^{14})_y & (x^{14})_z
\end{bmatrix}
\begin{bmatrix}
v^1_x \\
v^1_y \\
v^1_z
\end{bmatrix}
=
\begin{bmatrix}
v^{12} \\
v^{13} \\
v^{14}
\end{bmatrix} \notag
\end{equation}
この連立方程式を解くと節点 $1$ のベクトルが次のように表されます。
\begin{equation}
\boldsymbol{v}^1=\frac{1}{\Delta}\bigl([\boldsymbol{x}^{13}\times\boldsymbol{x}^{14}]v^{12}+[\boldsymbol{x}^{14}\times\boldsymbol{x}^{12}]v^{13}+[\boldsymbol{x}^{12}\times\boldsymbol{x}^{13}]v^{14}\bigr) \notag
\end{equation}
ここに $\Delta$ は(1.4-8)式で定義されています。(1.4-7)式の勾配をとると、
\begin{equation}
\begin{split}
&\boldsymbol{\nabla}N_1(\boldsymbol{x})=\frac{1}{\Delta}[\boldsymbol{x}^{24}\times\boldsymbol{x}^{23}] \hspace{10mm} \boldsymbol{\nabla}N_2(\boldsymbol{x})=\frac{1}{\Delta}[\boldsymbol{x}^{13}\times\boldsymbol{x}^{14}] \\
&\boldsymbol{\nabla}N_3(\boldsymbol{x})=\frac{1}{\Delta}[\boldsymbol{x}^{14}\times\boldsymbol{x}^{12}] \hspace{10mm} \boldsymbol{\nabla}N_4(\boldsymbol{x})=\frac{1}{\Delta}[\boldsymbol{x}^{12}\times\boldsymbol{x}^{13}]
\end{split} \notag
\end{equation}
となるので上の式は次のようにかくことが出来ます。
\begin{equation}
\boldsymbol{v}^1=\boldsymbol{\nabla}N_2v^{12}+\boldsymbol{\nabla}N_3v^{13}+\boldsymbol{\nabla}N_4v^{14} \notag
\end{equation}
同様にして他の節点におけるベクトルも次のように表すことが出来ます。
\begin{equation}
\begin{split}
&\boldsymbol{v}^2=\boldsymbol{\nabla}N_1v^{21}+\boldsymbol{\nabla}N_3v^{23}+\boldsymbol{\nabla}N_4v^{24} \\
&\boldsymbol{v}^3=\boldsymbol{\nabla}N_1v^{31}+\boldsymbol{\nabla}N_2v^{32}+\boldsymbol{\nabla}N_4v^{34} \\
&\boldsymbol{v}^4=\boldsymbol{\nabla}N_1v^{41}+\boldsymbol{\nabla}N_2v^{42}+\boldsymbol{\nabla}N_3v^{43} \\
\end{split} \notag
\end{equation}
まとめて次の式になります。
\begin{equation}
\boldsymbol{v}^\alpha=\sum_{\beta\ne\alpha}\boldsymbol{\nabla}N_\beta v^{\alpha\beta} \tag*{$(2.5-13)$}
\end{equation}
これを(2.5-11)式に代入すると要素内のベクトルを求めることが出来ます。
\begin{equation}
\begin{split}
\boldsymbol{v}&=\sum_{\alpha=1}^4N_\alpha\sum_{\beta\ne\alpha}\boldsymbol{\nabla}N_\beta v^{\alpha\beta} \\
&=N_1\bigl(\boldsymbol{\nabla}N_2v^{12}+\boldsymbol{\nabla}N_3v^{13}+\boldsymbol{\nabla}N_4v^{14}\bigr) \\
&+N_2\bigl(\boldsymbol{\nabla}N_1v^{21}+\boldsymbol{\nabla}N_3v^{23}+\boldsymbol{\nabla}N_4v^{24}\bigr) \\
&+N_3\bigl(\boldsymbol{\nabla}N_1v^{31}+\boldsymbol{\nabla}N_2v^{32}+\boldsymbol{\nabla}N_4v^{34}\bigr) \\
&+N_4\bigl(\boldsymbol{\nabla}N_1v^{41}+\boldsymbol{\nabla}N_2v^{42}+\boldsymbol{\nabla}N_3v^{43}\bigr)
\end{split} \notag
\end{equation}
ここで、$v^{\alpha\beta}=-v^{\beta\alpha}$ に注意すると次のようになります。
\begin{equation}
\begin{split}
\boldsymbol{v}&=(N_1\boldsymbol{\nabla}N_2-N_2\boldsymbol{\nabla}N_1)v^{12}+(N_2\boldsymbol{\nabla}N_3-N_3\boldsymbol{\nabla}N_2)v^{23} \\
&+(N_3\boldsymbol{\nabla}N_1-N_1\boldsymbol{\nabla}N_3)v^{31}+(N_1\boldsymbol{\nabla}N_4-N_4\boldsymbol{\nabla}N_1)v^{14} \\
&+(N_2\boldsymbol{\nabla}N_4-N_4\boldsymbol{\nabla}N_2)v^{24}+(N_3\boldsymbol{\nabla}N_4-N_4\boldsymbol{\nabla}N_3)v^{34}
\end{split} \notag
\end{equation}
これによって四面体の辺要素の補間関数が次のように求まりました。
\begin{equation}
\begin{split}
&\boldsymbol{N}_1=N_1\boldsymbol{\nabla}N_2-N_2\boldsymbol{\nabla}N_1 \hspace{10mm} \boldsymbol{N}_2=N_2\boldsymbol{\nabla}N_3-N_3\boldsymbol{\nabla}N_2 \\
&\boldsymbol{N}_3=N_3\boldsymbol{\nabla}N_1-N_1\boldsymbol{\nabla}N_3 \hspace{10mm} \boldsymbol{N}_4=N_1\boldsymbol{\nabla}N_4-N_4\boldsymbol{\nabla}N_1 \\
&\boldsymbol{N}_5=N_2\boldsymbol{\nabla}N_4-N_4\boldsymbol{\nabla}N_2 \hspace{10mm} \boldsymbol{N}_6=N_3\boldsymbol{\nabla}N_4-N_4\boldsymbol{\nabla}N_3 \\
\end{split} \tag*{$(2.5-14)$}
\end{equation}
辺番号を次のように定義します。
\begin{equation}
v^1=v^{12} \hspace{5mm} v^2=v^{23} \hspace{5mm} v^3=v^{31} \hspace{5mm} v^4=v^{14} \hspace{5mm} v^5=v^{24} \hspace{5mm} v^6=v^{34} \tag*{$(2.5-15)$}
\end{equation}
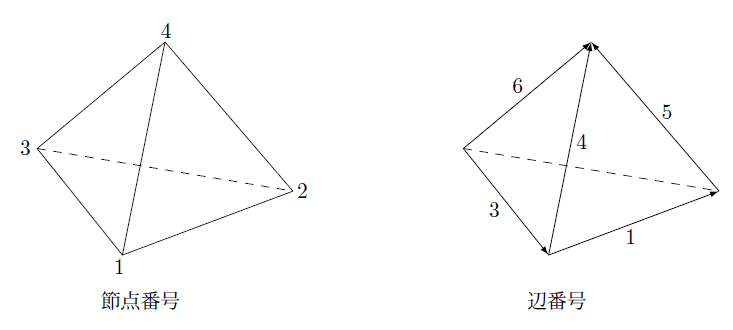
これより要素内のベクトルは次のように補間されます。
\begin{equation}
\boldsymbol{v}=\sum_{\alpha=1}^6\boldsymbol{N}_\alpha v^\alpha \tag*{$(2.5-16)$}
\end{equation}
ここに $\alpha$ は辺番号です。
技術情報 Techinicalinfo
- ホーム
- 技術情報
- 【技術情報】有限要素法入門
- 2.5 節点要素と辺要素
【技術情報】有限要素法入門
