まずベクトルについて基本的な復習をしておきます。ベクトルというのは方向と大きさを持った量で、具体的な例としては力や速度があります。ベクトルを表現するために下のような矢印で表し、向きを矢印の方向、大きさを矢印の長さで表現します。

ベクトルを表す記号としては太文字や頭に矢印を付けた次のような記号で表します。
\begin{equation}
\boldsymbol{v} \hspace{15mm} \vec{v} \notag
\end{equation}
ここではベクトルを表す文字は太文字とします。
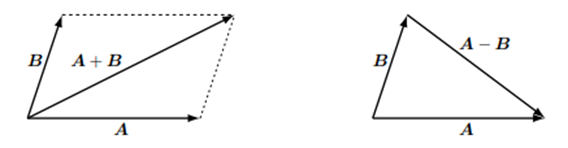
ベクトルの和や差は下の図に示すように二つのベクトルで作られる平行四辺形の対角線で表されるベクトルになります。
ベクトルは数との掛け算ができ、例えばベクトル $\boldsymbol{A}$ と数 $a$ との掛け算は $a\boldsymbol{A}$ と表し元のベクトルと方向は同じでベクトルの大きさが $a$ 倍になります。数 $a$ が正の場合は同じ向きで負の場合は逆向きになります。
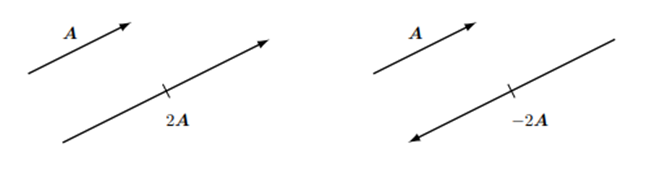
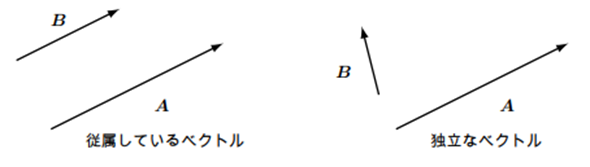
二つのベクトルが同じ方向すなわち、
\begin{equation}
\boldsymbol{A}=a\boldsymbol{B} \notag
\end{equation}
とかけるときはこれらのベクトルは従属であり、そうでない場合すなわちどのような数 $a$ でも、上のようにかけず、
\begin{equation}
\boldsymbol{A}\ne a\boldsymbol{B} \notag
\end{equation}
の場合は独立であるといいます。したがって独立なベクトルどうしは異なった方向を向いています。
次にベクトル空間の次元を考えます。独立なベクトルが一つしかないときは1次元空間といい、独立なベクトルが二つあるときは2次元空間、三つのときは3次元空間といいます。それぞれの空間ではどのようなベクトルも次元の数だけの独立なベクトルの和として表わすことができます。例えば2次元空間では独立なベクトルを $\boldsymbol{A}$ $\boldsymbol{B}$ とすればこの空間のベクトル $\boldsymbol{V}$ は、
\begin{equation}
\boldsymbol{V}=a\boldsymbol{A}+b\boldsymbol{B} \tag*{$(2-1)$}
\end{equation}
とかけます。ここで $a$ $b$ はベクトルによって一通りに決まる数です。
同様に3次元空間では独立なベクトルを $\boldsymbol{A}$ $\boldsymbol{B}$ $\boldsymbol{C}$ とすればこの空間内のベクトル $\boldsymbol{V}$ は、
\begin{equation}
\boldsymbol{V}=a\boldsymbol{A}+b\boldsymbol{B}+c\boldsymbol{C} \tag*{$(2-2)$}
\end{equation}
と表すことができます。
ベクトル空間における座標系を考えると、座標軸の数は空間の次元と一致します。そこで次の図のように座標軸方向に、大きさが $1$ である単位ベクトルを考え、これらのベクトルを基底ベクトルとよびます。
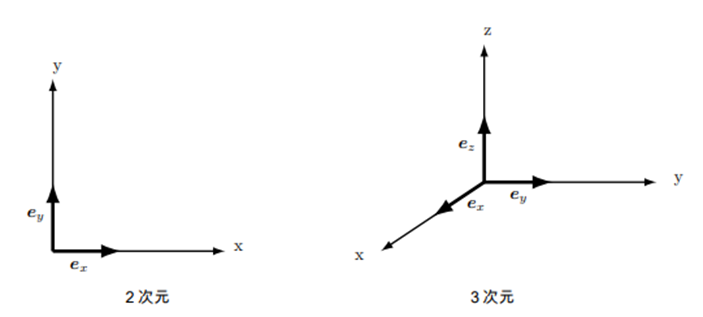
2次元空間の場合は基底ベクトルの組を $(\boldsymbol{e}_x,\boldsymbol{e}_y)$、また3次元の場合 $(\boldsymbol{e}_x,\boldsymbol{e}_y,\boldsymbol{e}_z)$ とかきます。このようにすればそれぞれの空間に属するベクトルは、
\begin{equation}
\begin{split}
&\boldsymbol{V}=V_x\boldsymbol{e}_x+V_y\boldsymbol{e}_y \\
&\boldsymbol{V}=V_x\boldsymbol{e}_x+V_y\boldsymbol{e}_y+V_z\boldsymbol{e}_z
\end{split} \tag*{$(2-3)$}
\end{equation}
とかくことができます。このように基底ベクトルを導入するとベクトルを特定するためにはこの係数を指定すればよいことになります。そこでこの係数をベクトルの成分とよび2次元の場合は $(V_x,V_y)$、3次元の場合は $(V_x,V_y,V_z)$ とかきます。このようにベクトルを成分で表すとベクトルに関する足し算や引き算は成分の関係として表わすことができます。
\begin{equation}
\begin{split}
&\boldsymbol{A}+\boldsymbol{B}=(A_x+B_x)\boldsymbol{e}_x+(A_y+B_y)\boldsymbol{e}_y+(A_z+B_z)\boldsymbol{e}_z \\
&\boldsymbol{A}-\boldsymbol{B}=(A_x-B_x)\boldsymbol{e}_x+(A_y-B_y)\boldsymbol{e}_y+(A_z-B_z)\boldsymbol{e}_z
\end{split} \notag
\end{equation}
成分で表示すると、
\begin{equation}
\begin{split}
&\boldsymbol{A}+\boldsymbol{B}=(A_x+B_x,A_y+B_y,A_z+B_z) \\
&\boldsymbol{A}-\boldsymbol{B}=(A_x-B_x,A_y-B_y,A_z-B_z)
\end{split} \tag*{$(2-4)$}
\end{equation}
となります。またベクトルの大きさはベクトルの絶対値とよび $|\boldsymbol{V}|$ とかき次のようになります。
\begin{equation}
|\boldsymbol{V}|=\sqrt{{V_x}^2+{V_y}^2+{V_z}^2} \tag*{$(2-5)$}
\end{equation}
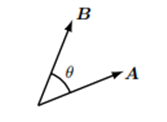
二つのベクトル $\boldsymbol{A}$ と $\boldsymbol{B}$ の内積 $\boldsymbol{A}\cdot\boldsymbol{B}$ は下の図のようにベクトル間の角度を $\theta$ とすれば、
次のように定義できます。
\begin{equation}
\boldsymbol{A}\cdot\boldsymbol{B}=|\boldsymbol{A}||\boldsymbol{B}|\mathrm{cos}\theta \tag*{$(2-6)$}
\end{equation}
この式の右辺はベクトルの成分によってかくことができ、
\begin{equation}
\boldsymbol{A}\cdot\boldsymbol{B}=A_xB_x+A_yB_y+A_zB_z \tag*{$(2-7)$}
\end{equation}
となります。この式は内積の定義式(2-6)式を使って示すことができます。これより内積には次の性質があることが分かります。
\begin{equation}
\begin{split}
&\boldsymbol{A}\cdot\boldsymbol{B}=\boldsymbol{B}\cdot\boldsymbol{A} \\
&\boldsymbol{A}\cdot(\boldsymbol{B}+\boldsymbol{C})=\boldsymbol{A}\cdot\boldsymbol{B}+\boldsymbol{A}\cdot\boldsymbol{C} \\
&\boldsymbol{A}\cdot\boldsymbol{A}=|\boldsymbol{A}|^2
\end{split} \tag*{$(2-8)$}
\end{equation}
次に二つのベクトル $\boldsymbol{A}$ と $\boldsymbol{B}$ の外積 $\boldsymbol{A}\times\boldsymbol{B}$ を考えます。内積と異なり外積の結果は新しいベクトルになります。下の図のようにベクトルの方向は元のベクトルと垂直であり、$\boldsymbol{A}$ から $\boldsymbol{B}$ へ回したとき右ねじに進む向きとなります。
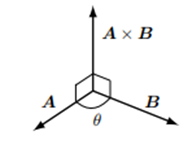
またベクトルの大きさは、
\begin{equation}
|\boldsymbol{A}\times\boldsymbol{B}|=|\boldsymbol{A}||\boldsymbol{B}|\mathrm{sin}\theta \tag*{$(2-9)$}
\end{equation}
となります。このベクトルの成分は元のベクトルの成分を使って次のように表すことができます。
\begin{equation}
\begin{split}
&[\boldsymbol{A}\times\boldsymbol{B}]_x=A_yB_z-A_zB_y \\
&[\boldsymbol{A}\times\boldsymbol{B}]_y=A_zB_x-A_xB_z \\
&[\boldsymbol{A}\times\boldsymbol{B}]_z=A_xB_y-A_yB_x
\end{split} \tag*{$(2-10)$}
\end{equation}
この関係は外積の定義(2-9)式から導くことができます。これより外積に関して次の関係があることが分かります。
\begin{equation}
\begin{split}
&\boldsymbol{A}\times\boldsymbol{B}=-\boldsymbol{B}\times\boldsymbol{A} \\
&\boldsymbol{A}\times(\boldsymbol{B}+\boldsymbol{C})=\boldsymbol{A}\times\boldsymbol{B}+\boldsymbol{A}\times\boldsymbol{C} \\
&\boldsymbol{A}\times\boldsymbol{A}=0
\end{split} \tag*{$(2-11)$}
\end{equation}
このように成分を使って表すとベクトルの計算がいちいち図をかかなくてもできるので便利です。ここで和の記号を使うために成分の添字記号 $x$ $y$ $z$ を数字の $1$ $2$ $3$ とします。これよりベクトルを成分で表す場合、
\begin{equation}
\begin{split}
\boldsymbol{V}&=V_x\boldsymbol{e}_x+V_y\boldsymbol{e}_y+V_z\boldsymbol{e}_z \\
&=V_1\boldsymbol{e}_1+V_2\boldsymbol{e}_2+V_3\boldsymbol{e}_3 \\
&=\sum_{i=1}^3V_i\boldsymbol{e}_i
\end{split} \tag*{$(2-12)$}
\end{equation}
とかけます。また内積は次のようになります。
\begin{equation}
\boldsymbol{A}\cdot\boldsymbol{B}=\sum_{i=1}^3A_iB_i \tag*{$(2-13)$}
\end{equation}
直交座標の場合基底ベクトルの内積は次のようになります。
\begin{equation}
\begin{split}
&\boldsymbol{e}_1\cdot\boldsymbol{e}_1=\boldsymbol{e}_2\cdot\boldsymbol{e}_2=\boldsymbol{e}_3\cdot\boldsymbol{e}_3=1 \\
&\boldsymbol{e}_i\cdot\boldsymbol{e}_j=0 \hspace{10mm} (i\ne j)
\end{split} \tag*{$(2-14)$}
\end{equation}
これより例えば、
\begin{equation}
\begin{split}
\boldsymbol{e}_1\cdot\boldsymbol{V}&=\boldsymbol{e}_1\cdot(V_1\boldsymbol{e}_1+V_2\boldsymbol{e}_2+V_3\boldsymbol{e}_3) \\
&=V_1\boldsymbol{e}_1\cdot\boldsymbol{e}_1+V_2\boldsymbol{e}_2\cdot\boldsymbol{e}_1+V_3\boldsymbol{e}_3\cdot\boldsymbol{e}_1 \\
&=V_1
\end{split} \tag*{$(2-15)$}
\end{equation}
となるのでベクトルの成分は次のように表すことができます。
\begin{equation}
V_i=\boldsymbol{e}_i\cdot\boldsymbol{V} \tag*{$(2-16)$}
\end{equation}
これを使うとベクトルを成分でかいた(2-12)式は次のようにかけます。
\begin{equation}
\boldsymbol{V}=\sum_{i=1}^3(\boldsymbol{e}_i\cdot\boldsymbol{V})\boldsymbol{e}_i \tag*{$(2-17)$}
\end{equation}
ベクトルの復習はひとまずこれで終えて次に微分と積分について復習します。次のような関数の勾配を考えます。
\begin{equation}
y=f(x) \tag*{$(2-18)$}
\end{equation}
区間 $[x,x+h]$ における平均の勾配は次のように表すことができます。
\begin{equation}
平均勾配=\frac{f(x+h)-f(x)}{h} \tag*{$(2-19)$}
\end{equation}
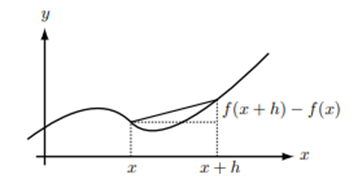
この区間を狭めていき区間幅$h$をゼロに近づけてゆけば座標 $x$ における勾配が求まります。この勾配のことを関数の座標 $x$ における微係数とよび次のようにかきます。
\begin{equation}
勾配=\lim_{h\rightarrow 0}\frac{f(x+h)-f(x)}{h}=\frac{d}{dx}f(x) \tag*{$(2-20)$}
\end{equation}
この勾配も座標 $x$ の関数となっていますのでこれを導関数とよんでいます。微分はとっつきにくいと思われる方もおられますが、このように関数の勾配と考えれば素直に理解できると思います。
微分に関するここまでは高校の数学で学んだ内容ですが、次に2変数の関数を考えます。
\begin{equation}
z=f(x,y) \tag*{$(2-21)$}
\end{equation}
このとき、この関数の勾配といっても一通りには決まりません。勾配は一定の距離進んだとき関数の値がどう変化するかということであり、1変数の場合はこの方向は決まっていました。ところが2変数の場合変数の動く空間は2次元なので関数の勾配を考えるためには方向を指定してやる必要があります。そこで次の二方向の勾配を考えます。
\begin{equation}
\begin{split}
&x方向の平均勾配=\frac{f(x+h,y)-f(x,y)}{h} \\
&y方向の平均勾配=\frac{f(x,y+h)-f(x,y)}{h}
\end{split} \notag
\end{equation}
1変数の場合と同様に平均をとる区間を小さくした極限で座標 $(x,y)$ における2種類の勾配が求まります。この勾配を求める操作を偏微分とよび次のようにかきます。
\begin{equation}
\begin{split}
&\frac{\partial}{\partial x}f(x,y)=\lim_{h\rightarrow 0}\frac{f(x+h,y)-f(x,y)}{h} \\
&\frac{\partial}{\partial y}f(x,y)=\lim_{h\rightarrow 0}\frac{f(x,y+h)-f(x,y)}{h}
\end{split} \tag*{$(2-22)$}
\end{equation}
例えでいえば山の中腹に立った時、東向き($x$ 方向)の勾配と北向き($y$ 方向)の勾配を求める操作が偏微分ということになります。ところでこの場合東向きや北向きが一番きつい勾配であるとは限りません。私たちが普段使っている勾配とは、この地点にボールを置いたときボールが転がる方向であり、その方向の高さの変化を指しています。それではこの勾配と先に求めた $x$ 方向、$y$ 方向の勾配である偏微分はどのような関係があるのでしょうか。
それを見るために山の斜面が平面であるとみなせるぐらい小さな領域を考えます。地球は球面なので地図を作るにはそのことを考える必要があるのですが、家の近所の地図を作るのであれば平面にかいてやればよいのと同じで、なめらかな曲面では十分小さな領域は平面とみなすことができます。
平面は3点を与えれば求めることができます。ここで平面の方程式を、
\begin{equation}
z=f(x,y)=ax+by+c \tag*{$(2-23)$}
\end{equation}
とします。ここで3点の座標として $(x_0,y_0)$ $(x_0+\Delta x,y_0)$ $(x_0,y_0+\Delta y)$ をとると上の式はそれぞれ次のようになります。
\begin{equation}
\begin{split}
&f(x_0,y_0)=ax_0+by_0+c \\
&f(x_0+\Delta x,y_0)=a(x_0+\Delta x)+by_0+c \\
&f(x_0,y_0+\Delta y)=ax_0+b(y_0+\Delta y)+c
\end{split} \notag
\end{equation}
これより(2-23)式の係数が次のように求まります。
\begin{equation}
\begin{split}
&a=\frac{f(x_0+\Delta x,y_0)-f(x_0,y_0)}{\Delta x}\Rightarrow\frac{\partial f}{\partial x} \\
&b=\frac{f(x_0,y_0+\Delta y)-f(x_0,y_0)}{\Delta y}\Rightarrow\frac{\partial f}{\partial y} \\
&c=f(x_0,y_0)-\frac{\partial f}{\partial x}x_0-\frac{\partial f}{\partial y}y_0
\end{split} \tag*{$(2-24)$}
\end{equation}
したがって(2-23)式は次のようにかけます。
\begin{equation}
f(x,y)=f(x_0,y_0)+\frac{\partial f}{\partial x}(x-x_0)+\frac{\partial f}{\partial y}(y-y_0) \tag*{$(2-25)$}
\end{equation}
この式を見ると座標 $(x_0,y_0)$ から $(x,y)$ に移動したときの変化率がこの式の右辺の第2項第3項で表されていることが分かります。そこで移動ベクトル、
\begin{equation}
\boldsymbol{r}=(x-x_0,y-y_0) \tag*{$(2-26)$}
\end{equation}
と勾配ベクトル、
\begin{equation}
\boldsymbol{g}=\bigl(\frac{\partial f}{\partial x},\frac{\partial f}{\partial y}\bigr) \tag*{$(2-27)$}
\end{equation}
を導入すると、変化はこのベクトルの内積によって表わすことができます。
\begin{equation}
f(x,y)=f(x_0,y_0)+\boldsymbol{g}\cdot\boldsymbol{r} \tag*{$(2-28)$}
\end{equation}
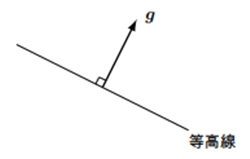
関数が変化しない方向は、
\begin{equation}
\boldsymbol{g}\cdot\boldsymbol{r}=0 \tag*{$(2-29)$}
\end{equation}
であり等高線の方向と一致します。したがってベクトル $\boldsymbol{g}$ は等高線と直交する方向、すなわち最も勾配が急な方向を向いていることが分かります。
ここで述べたことはそのまま3変数関数に拡張することができます。3変数関数の場合(2-25)式は次のようになります。
\begin{equation}
f(x,y,z)=f(x_0,y_0,z_0)+\frac{\partial f}{\partial x}(x-x_0)+\frac{\partial f}{\partial y}(y-y_0)
+\frac{\partial f}{\partial z}(z-z_0) \tag*{$(2-30)$}
\end{equation}
この関数の具体例は3次元空間に分布する温度や密度です。このとき勾配ベクトルと移動ベクトルはそれぞれ次のようになります。
\begin{equation}
\begin{split}
&\boldsymbol{g}=\bigl(\frac{\partial f}{\partial x},\frac{\partial f}{\partial y},\frac{\partial f}{\partial z}\bigr) \\
&\boldsymbol{r}=(x-x_0,y-y_0,z-z_0)
\end{split} \tag*{$(2-31)$}
\end{equation}
このときは、
\begin{equation}
\boldsymbol{g}\cdot\boldsymbol{r}=0 \tag*{$(2-32)$}
\end{equation}
をみたす点は等高面となります。一般的には、
\begin{equation}
\mathrm{grad}f\equiv\bigl(\frac{\partial f}{\partial x},\frac{\partial f}{\partial y},\frac{\partial f}{\partial z}\bigr) \tag*{$(2-33)$}
\end{equation}
を関数 $f$ の勾配ベクトルとよんでいます。先ほどの温度や密度の拡散は経験的には一番大きな勾配方向つまり $\mathrm{grad}f$ の方向であることが知られています。
次に積分に移ります。関数、
\begin{equation}
y=f(x) \tag*{$(2-34)$}
\end{equation}
の区間 $[a,b]$ における定積分を次のようにかきます。
\begin{equation}
\int_a^bf(x)dx \notag
\end{equation}
この積分は積分区間で横軸 $x$ 軸と、縦軸 $y$ 軸で表される関数値とで囲まれる面積となります。この面積を求めるには、次の図に示すように区間 $[a,b]$ を $n$ 等分し幅 $h$ の小区間に分割しその区間の端点における関数の値と区間幅 $h$ をかけて長方形の面積を出し、その長方形を足し合わせます。
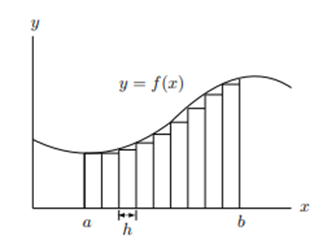
この長方形の面積の和は、
\begin{equation}
\sum_{i=1}^nf(x_i)h \notag
\end{equation}
となります。ただし図から分かるようにこれは $x$ 軸と関数 $f(x)$ に囲まれた面積と一致しませんが、分割数を大きくして分割幅 $h$ を小さくすればするほど近づきゼロとなる極限をとれば一致します。これより積分値は次のようにして計算できます。
\begin{equation}
\int_a^bf(x)dx=\lim_{h\rightarrow 0}\sum_{i=1}^nf(x_i)h \notag
\end{equation}
この方法を区分求積法とよんでいます。
具体的な例を示します。長さ $10\mathrm{\,cm}$ の細い糸があり $1\mathrm{\,cm}$ あたりの重さが $0.2 \mathrm{\,g}$ とするとこの糸の重さは $2\mathrm{\,g}$ となります。
糸を横にまっすぐ伸ばして置き左端を原点とし糸の方向に $x$ 軸をとると糸の重さは積分を使って次のようにかけます。
\begin{equation}
糸の重さ=\int_0^{10}0.2dx=2 \notag
\end{equation}
このとき積分される関数は $1\mathrm{\,cm}$ あたりの糸の重さであり一定なので、この積分はこれと積分区間を掛け合わせることによって簡単に求まったのです。もし糸の単位長さ当たりの重さ、すなわち線密度が場所によって異なっていたらこのように簡単にはいきません。例えばこの線密度を表す関数が、
\begin{equation}
f(x)=0.02x+0.1 \notag
\end{equation}
とすれば上の積分は次のようになります。
\begin{equation}
\int_0^{10}(0.02x+0.1)dx=\bigl[0.02\times\frac{1}{2}x^2+0.1x\bigr]_0^{10}=2 \notag
\end{equation}
この程度であれば高校で習った積分の知識があれば十分できます。ところが糸の線密度がもっと複雑な関数であった場合はどうでしょうか。高校の知識では計算できない場合があります。積分が難しいと感じるのはこのように積分を具体的に計算するときです。積分の教科書にはこのような積分を行うための多くのテクニックがかかれておりそれを習得するのが大変だからです。
今後は積分を具体的に計算することがないのでこのようなテクニックを使うことはありません。むしろ積分が意味していることを直感的に理解するのが重要だと思われます。今述べた例の場合は糸の線密度が関数として与えられておりそれを積分したものは糸の重さになります。
次に2変数関数の定積分を考えます。
\begin{equation}
\int_c^d\int_a^bf(x,y)dxdy=\int_c^d\bigl[\int_a^bf(x,y)dx\bigr]dy \notag
\end{equation}
この積分は積分の中に積分が入っている形をしているので2重積分といいます。まず $y$ 座標が決まっている場合は次の積分ができます。
\begin{equation}
g(y)=\int_a^bf(x,y)dx \notag
\end{equation}
この積分は変数 $x$ による1変数の積分なので計算でき結果的に $y$ の関数である左辺が求まります。次にこの関数を $y$ で積分すれば上の2変数関数の積分が求まります。
\begin{equation}
\int_c^d\int_a^bf(x,y)dxdy=\int_c^dg(y)dy \notag
\end{equation}
このように1変数の積分では面積が求まったのですが2変数関数の積分では座標面 $xy$ と $z$ 軸で表される関数値の間の体積が求まることになります。ここで積分される範囲は $x$ 座標の区間 $[a,b]$ と $y$ 座標の区間 $[c,d]$ で囲まれる長方形の領域となります。先ほどの糸の重さの例と同様に考えるとこの座標面に置かれた薄い平板の面密度は座標 $xy$ の関数となるので2重積分を行うことによって重さが求まります。
同様にして3変数関数の積分は、
\begin{equation}
\int_e^f\int_c^d\int_a^bf(x,y,z)dxdydz \notag
\end{equation}
とかき3重積分といいます。ここで積分される領域すなわち $x$ 座標の区間 $[a,b]$、$y$ 座標の区間 $[c,d]$ そして $z$ 座標の区間 $[e,f]$ で囲まれた直方体の中に物体があり、その物体の密度をこの関数が表しているとすればこの積分はこの物体の重さになります。
ここまでの話はそれほど飛躍がなかったと思います。電磁気であらわれる積分はたいていこの3重積分までですが、積分区間が直線ではなく曲線上の積分や平面上の積分や球面のような曲面上の積分が必要になるので、次にその話をします。
最初1変数の積分では $x$ 軸上の積分を考えたのですが、例で取り上げた糸が直線ではなく曲がっている場合、この糸の重さをどう求めたらよいでしょうか。この場合は糸の端点からの距離を糸の各点に対応付けてパラメータとします。これが $x$ 座標に対応しているのでこのパラメータを $s$ とかくとこのパラメータによる積分となります。
\begin{equation}
\int_a^bf(s)ds \notag
\end{equation}
ここでの積分範囲を表す文字 $a$ $b$ は座標の値ではなくこのパラメータの値となります。この積分は $x$ 軸上の積分を区間を細かく分割してそれぞれの小区間で関数値と区間の長さをかけたものの和を求め、分割された区間の長さがゼロとなる極限から求めるという区分求積法と同じ方法で求めることができます。
次の図に示すように積分する線を小区間に分割し、端部からはかった距離であるパラメータ $s$ が $a$ である点から $b$ である点まで関数値とこの小区間の長さ $\Delta s$ をかけて足し合わせます。そのあとで $\Delta s$ をゼロにする極限をとります。
\begin{equation}
\int_a^bf(s)ds=\lim_{\Delta s\rightarrow 0}\sum_if(s_i)\Delta s \notag
\end{equation}
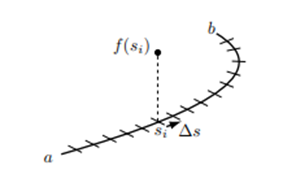
輪ゴムのようなループ状のものであれば一周だけ積分します。このような積分を周回積分とよび次のように表します。
\begin{equation}
\oint f(s)ds \notag
\end{equation}
電磁気学ではこのように曲線上で積分することが多々あります。例えば電線内での電圧降下を計算する場合、直線電流でない限り電線に沿った電場を曲線上で積分する必要があります。また磁束が変化したときにはその周りに電圧が発生しますがその電圧は磁束を取り囲む電場を周回積分したものになります。
次に2重積分の場合ですが、積分領域が平面でない場合があります。例えば薄いゴムでできた半径 $R$ のボールの重さを求めるには、ゴムの厚みと密度の積をゴムの表面で積分してやる必要があります。
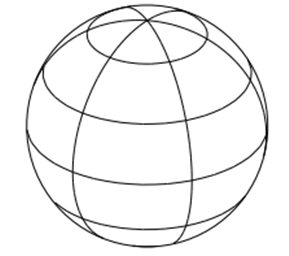
このような積分を次のようにかきます。
\begin{equation}
\iint_S\rho hdS \notag
\end{equation}
ここで $\rho$ はゴムの密度、$h$ はゴムの厚みで一般にはボール表面の場所の関数です。もしこれらが一定であれば上の積分は簡単に次のようになります。
\begin{equation}
\iint_S\rho hdS=4\pi R^2\rho h \notag
\end{equation}
ここで積分記号の下についている記号 $S$ は積分領域つまりボールの球面を表しています。また $dS$ は面積分の面素を表しており $xy$ 面上の積分のときの $dxdy$ に対応しています。
技術情報 Techinicalinfo
- ホーム
- 技術情報
- 【技術情報】ベクトル解析入門
- 2. 基礎的な準備
【技術情報】ベクトル解析入門
