有限要素法を使ってこの問題へのアプローチを行います。
有限要素法の場合ここで分割した区間幅 $\Delta x$ の領域を要素とよび区間幅は一定でなくてもかまいません。また要素を分割する $x_i$ などの点を節点とよんでいます。
有限要素法の場合はこの要素内部でポテンシャルを節点の値で内挿します。下の図は区間 $[x_i,x_{i+1}]$ の要素ですが、座標 $x_i$ におけるポテンシャルの値 $\phi_i$ と、座標 $x_{i+1}$ におけるポテンシャルの値 $\phi_{i+1}$ によって座標 $x$ におけるポテンシャルを内挿します。
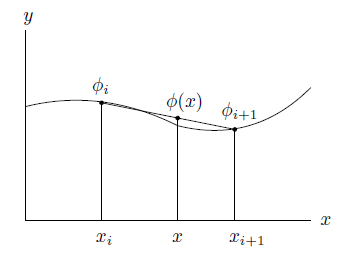
この場合は線形補間なので次のようになります。
\begin{equation}
\phi(x)=\frac{x_{i+1}-x}{x_{i+1}-x_i}\phi_i+\frac{x-x_i}{x_{i+1}-x_i}\phi_{i+1} \notag
\end{equation}
ここで次の補間関数を定義します。
\begin{equation}
\begin{split}
&N_1(x)=\frac{x_{i+1}-x}{x_{i+1}-x_i} \\
&N_2(x)=\frac{x-x_i}{x_{i+1}-x_i}
\end{split} \tag*{$(1.2-1)$}
\end{equation}
つまり座標 $x_i$ のこの要素におけるローカルな番号を $1$、座標 $x_{i+1}$ のこの要素におけるローカルな番号を $2$ として、
\begin{equation}
\phi^1=\phi_i \hspace{10mm} \phi^2=\phi_{i+1} \notag
\end{equation}
とおけば、要素内のポテンシャルは次のようにかけます。
\begin{equation}
\phi(x)=\sum_{\alpha=1}^2N_\alpha(x)\phi^\alpha \tag*{$(1.2-2)$}
\end{equation}
問題は1次元の静電場の方程式(1.1-7)式を解くことです。もし誘電率が一定ならば(1.1-7)式は次のようにかけます。
\begin{equation}
\frac{d}{dx}\bigl(\frac{d\phi}{dx}\bigr)=-\frac{\rho}{\epsilon} \notag
\end{equation}
これに要素内で内挿したポテンシャル(1.2-2)式を代入すると左辺は、
\begin{equation}
\frac{d}{dx}\frac{\phi_{i+1}-\phi_i}{x_{i+1}-x_i}=0 \notag
\end{equation}
となり意味のない方程式となってしまいます。これは補間関数が1次であるのに対して方程式が2階の微分方程式となっているからです。
このようなことを避けるために有限要素法では基礎方程式の微分の階数を減らすことを行います。
(1.1-7)に戻って、この方程式の両辺に任意の関数 $w(x)$ をかけて解析区間 $[a,b]$ で積分します。
\begin{equation}
\int_a^bw(x)\frac{d}{dx}\bigl(\epsilon\frac{d\phi}{dx}\bigr)dx=-\int_a^bw(x)\rho dx \notag
\end{equation}
$w$ が任意関数のときこの式は元の式(1.1-7)式と等価な式です。
ここで左辺を部分積分を使って次のように変形します。
\begin{equation}
\begin{split}
\int_a^b\frac{d}{dx}\bigl(w(x)\epsilon\frac{d\phi}{dx}\bigr)dx-\int_a^b\frac{dw}{dx}\epsilon\frac{d\phi}{dx}dx
=\bigl[w(x)\epsilon\frac{d\phi}{dx}\bigr]_a^b-\int_a^b\frac{dw}{dx}\epsilon\frac{d\phi}{dx}dx
\end{split} \notag
\end{equation}
境界点 $a$、$b$ で電場がゼロの場合は $d\phi/dx=0$ となるのでこの右辺第1項はゼロとなります。
また後で示しますがこれらの点でポテンシャルが決まっている場合もこの項はゼロとなります。
したがって基礎方程式は次のようにかきかえることができます。
\begin{equation}
\int_a^b\frac{dw}{dx}\epsilon\frac{d\phi}{dx}dx=\int_a^bw(x)\rho dx \tag*{$(1.2-3)$}
\end{equation}
ここで解析領域 $[a,b]$ を先ほどのように小領域である要素に分割します。積分はこれらの要素ごとの積分の和で表すことができます。
分割数が $n$ の場合は次のようになります。
\begin{equation}
\sum_{i=1}^n\int_{x_i}^{x_{i+1}}\frac{dw}{dx}\epsilon\frac{d\phi}{dx}dx=\sum_{i=1}^n\int_{x_i}^{x_{i+1}}w(x)\rho dx \tag*{$(1.2-4)$}
\end{equation}
それぞれの要素内部ではポテンシャルは(1.2-1)式の補間関数によって(1.2-2)式のように表すことができます。
また関数 $w(x)$ についても同じように補間します。
\begin{equation}
w(x)=\sum_{\alpha=1}^2N_\alpha(x)w^\alpha \tag*{$(1.2-5)$}
\end{equation}
これを(1.2-4)式に代入するとこの式の左辺と右辺は次のようになります。
\begin{equation}
\begin{split}
&\sum_i\sum_{\alpha\beta}w^{i\alpha}\int_{x_i}^{x_{i+1}}\frac{dN_\alpha}{dx}\epsilon\frac{dN_\beta}{dx}dx\phi^{i\beta} \\
&\sum_i\sum_{\alpha}w^{i\alpha}\int_{x_i}^{x_{i+1}}N_\alpha\rho dx
\end{split} \notag
\end{equation}
ここで $\alpha$、$\beta$ は要素内の節点につけたローカルな番号 $1$、$2$ ですが、ポテンシャルや $w$ の肩についている添字 $i\alpha$、$i\beta$ などは
節点についているグローバルな番号 $i$、$i+1$ などです。
ここで次の要素行列と要素ベクトルを定義します。
\begin{equation}
\begin{split}
&K_{\alpha\beta}^{(i)}=\int_{x_i}^{x_{i+1}}\frac{dN_\alpha}{dx}\epsilon\frac{N_\beta}{dx}dx \\
&F_\alpha^{(i)}=\int_{x_i}^{x_{i+1}}N_\alpha\rho dx
\end{split} \tag*{$(1.2-6)$}
\end{equation}
これより(1.2-4)式は、
\begin{equation}
\sum_i\sum_{\alpha\beta}w^{i\alpha}K_{\alpha\beta}^{(i)}\phi^{i\beta}=\sum_i\sum_\alpha w^{i\alpha}F_\alpha^{(i)} \notag
\end{equation}
となります。さらに関数 $w$ でまとめると次のようになります。
\begin{equation}
\sum_i\sum_{\alpha}w^{i\alpha}\bigl(\sum_\beta K_{\alpha\beta}^{(i)}\phi^{i\beta}-F_\alpha^{(i)}\bigr)=0 \tag*{$(1.2-7)$}
\end{equation}
この式は要素番号 $i$ と要素内のローカルな節点番号 $\alpha$ の和になっていますが、
$w^{i\alpha}$ はグローバルな節点番号 $i$ と $i+1$ に対応しています。
この関係を領域を4要素に分割した下の図を基に説明します。
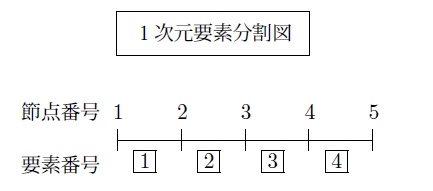
解析領域である線分を4分割し上に節点番号、下の四角で囲った番号で要素番号を示しています。
この場合について(1.2-7)式の左辺をかきくだすと次のようになります。
\begin{equation}
\begin{split}
&w^{11}(K_{11}^{(1)}\phi^{11}+K_{12}^{(1)}\phi^{12}-F_1^{(1)})+w^{12}(K_{21}^{(1)}\phi^{11}+K_{22}^{(1)}\phi^{12}-F_2^{(1)}) \\
+&w^{21}(K_{11}^{(2)}\phi^{21}+K_{12}^{(2)}\phi^{22}-F_1^{(2)})+w^{22}(K_{21}^{(2)}\phi^{21}+K_{22}^{(2)}\phi^{22}-F_2^{(2)}) \\
+&w^{31}(K_{11}^{(3)}\phi^{31}+K_{12}^{(3)}\phi^{32}-F_1^{(3)})+w^{32}(K_{21}^{(3)}\phi^{31}+K_{22}^{(3)}\phi^{32}-F_2^{(3)}) \\
+&w^{41}(K_{11}^{(4)}\phi^{41}+K_{12}^{(4)}\phi^{42}-F_1^{(4)})+w^{42}(K_{21}^{(4)}\phi^{41}+K_{22}^{(4)}\phi^{42}-F_2^{(4)})
\end{split} \notag
\end{equation}
図を見ると要素番号 $i$ の第1節点は節点番号 $i$、第2節点は節点番号 $i+1$ となっています。例えば要素番号1の第2節点は2であり2番目の要素の第1節点と同じです。
このように要素番号とローカルな節点番号の組 $(i,\alpha)$ をグローバルな節点番号にかきなおすと(1.2-7)式の左辺は次のようにかきなおすことが出来ます。
\begin{equation}
\begin{split}
&w^{1}(K_{11}^{(1)}\phi^{1}+K_{12}^{(1)}\phi^{2}-F_1^{(1)})+w^{2}(K_{21}^{(1)}\phi^{1}+K_{22}^{(1)}\phi^{2}-F_2^{(1)}) \\
+&w^{2}(K_{11}^{(2)}\phi^{2}+K_{12}^{(2)}\phi^{3}-F_1^{(2)})+w^{3}(K_{21}^{(2)}\phi^{2}+K_{22}^{(2)}\phi^{3}-F_2^{(2)}) \\
+&w^{3}(K_{11}^{(3)}\phi^{3}+K_{12}^{(3)}\phi^{4}-F_1^{(3)})+w^{4}(K_{21}^{(3)}\phi^{3}+K_{22}^{(3)}\phi^{4}-F_2^{(3)}) \\
+&w^{4}(K_{11}^{(4)}\phi^{4}+K_{12}^{(4)}\phi^{5}-F_1^{(4)})+w^{5}(K_{21}^{(4)}\phi^{4}+K_{22}^{(4)}\phi^{5}-F_2^{(4)})
\end{split} \notag
\end{equation}
ここに現れる $w^1$ から $w^5$ は任意関数を離散化した値です。したがって上の式がゼロになるにはこれらの係数がそれぞれゼロになる必要があります。
したがって(1.2-7)式をみたすには次の方程式が成り立つ必要があります。
\begin{equation}
\begin{split}
&K_{11}^{(1)}\phi^{1}+K_{12}^{(1)}\phi^{2}=F_1^{(1)} \\
&K_{21}^{(1)}\phi^{1}+(K_{22}^{(1)}+K_{11}^{(2)})\phi^{2}+K_{12}^{(2)}\phi^{3}=F_2^{(1)}+F_1^{(2)} \\
&K_{21}^{(2)}\phi^{2}+(K_{22}^{(2)}+K_{11}^{(3)})\phi^{3}+K_{12}^{(3)}\phi^{4}=F_2^{(2)}+F_1^{(3)} \\
&K_{21}^{(3)}\phi^{3}+(K_{22}^{(3)}+K_{11}^{(4)})\phi^{4}+K_{12}^{(4)}\phi^{5}=F_2^{(3)}+F_1^{(4)} \\
&K_{21}^{(4)}\phi^{4}+K_{22}^{(4)}\phi^{5}=F_2^{(4)}
\end{split} \tag*{$(1.2-8)$}
\end{equation}
これでグローバルな節点番号に対応したスカラーポテンシャルに対する連立方程式が得られました。
行列でかくと次のようになります。
\begin{equation}
\begin{bmatrix}
K_{11}^{(1)} & K_{12}^{(1)} & 0 & 0 & 0 \\
K_{21}^{(1)} & (K_{22}^{(1)}+K_{11}^{(2)}) & K_{12}^{(2)} & 0 & 0 \\
0 & K_{21}^{(2)} & (K_{22}^{(2)}+K_{11}^{(3)}) & K_{12}^{(3)} & 0 \\
0 & 0 & K_{21}^{(3)} & (K_{22}^{(3)}+K_{11}^{(4)}) & K_{12}^{(4)} \\
0 & 0 & 0 & K_{21}^{(4)} & K_{22}^{(4)}
\end{bmatrix}
\begin{bmatrix}
\phi^{1} \\
\phi^{2} \\
\phi^{3} \\
\phi^{4} \\
\phi^{5}
\end{bmatrix}
=
\begin{bmatrix}
F_1^{(1)} \\
F_2^{(1)}+F_1^{(2)} \\
F_2^{(2)}+F_1^{(3)} \\
F_2^{(3)}+F_1^{(4)} \\
F_2^{(4)}
\end{bmatrix} \tag*{$(1.2-9)$}
\end{equation}
この連立方程式を解けば節点におけるスカラーポテンシャルの値が分かりそれをもとに要素内の電場などが求まります。
この方程式を見るとここに現れる行列の要素は要素行列や要素ベクトルから構成されていることが分かります。
したがってこのようなグローバルな方程式を作るには、まず要素ごとの要素行列と要素ベクトルを求めておき、そのローカルな節点番号が対応するグローバルな節点に割り振ることによってこのような方程式を作成することが出来ます。
ここで要素行列を具体的に求めておきます。
補間関数に関する(1.2-1)式から、
\begin{equation}
\begin{split}
&\frac{dN_1}{dx}=-\frac{1}{x_{i+1}-x_i} \\
&\frac{dN_2}{dx}=+\frac{1}{x_{i+1}-x_i}
\end{split} \notag
\end{equation}
ですから、要素内で誘電率が一定であれば(1.2-6)式の要素行列の積分内は一定値となり、$\Delta x=x_{i+1}-x_i$ とかけば次のようになります。
\begin{equation}
K_{\alpha\beta}=
\begin{bmatrix}
\frac{\epsilon}{\Delta x} & -\frac{\epsilon}{\Delta x} \\
-\frac{\epsilon}{\Delta x} & \frac{\epsilon}{\Delta x}
\end{bmatrix} \tag*{$(1.2-10)$}
\end{equation}
また要素内で電荷密度が一定とすれば要素ベクトルは、
\begin{equation}
F_\alpha=
\begin{bmatrix}
\frac{\rho}{2}\Delta x \\
\frac{\rho}{2}\Delta x
\end{bmatrix} \tag*{$(1.2-11)$}
\end{equation}
です。これをみると要素内の電荷量 $\rho\Delta x$ を二つの節点に割り振った形になっています。
解析領域を4分割した先の例では誘電率と電荷密度を一定とすれば、(1.2-9)式は次のようになります。
\begin{equation}
\frac{\epsilon}{\Delta x}
\begin{bmatrix}
1 & -1 & 0 & 0 & 0 \\
-1 & 2 & -1 & 0 & 0 \\
0 & -1 & 2 & -1 & 0 \\
0 & 0 & -1 & 2 & -1 \\
0 & 0 & 0 & -1 & 1
\end{bmatrix}
\begin{bmatrix}
\phi^{1} \\
\phi^{2} \\
\phi^{3} \\
\phi^{4} \\
\phi^{5}
\end{bmatrix}
=\frac{\rho}{2}\Delta x
\begin{bmatrix}
1 \\
2 \\
2 \\
2 \\
1
\end{bmatrix} \notag
\end{equation}
解析領域を $[0,1]$ としたときの解析解は(1.1-10)式ですが、この場合の境界条件は、
\begin{equation}
\begin{split}
&E=-\frac{d\phi}{dx}=0 \hspace{10mm} (x=0) \\
&\phi=0 \hspace{32mm} (x=1)
\end{split} \notag
\end{equation}
ですが最初の条件は境界積分を入れない場合自動的に満たしているので、ポテンシャルに関する条件、
\begin{equation}
\phi^{5}=0 \notag
\end{equation}
を考慮する必要があります。これは連立方程式を次のように縮小することで満たすことが出来ます。
\begin{equation}
\frac{\epsilon}{\Delta x}
\begin{bmatrix}
1 & -1 & 0 & 0 \\
-1 & 2 & -1 & 0 \\
0 & -1 & 2 & -1 \\
0 & 0 & -1 & 2
\end{bmatrix}
\begin{bmatrix}
\phi^{1} \\
\phi^{2} \\
\phi^{3} \\
\phi^{4}
\end{bmatrix}
=\frac{\rho}{2}\Delta x
\begin{bmatrix}
1 \\
2 \\
2 \\
2
\end{bmatrix} \notag
\end{equation}
これを解くと次のようになります。
\begin{equation}
\begin{bmatrix}
\phi^{1} \\
\phi^{2} \\
\phi^{3} \\
\phi^{4}
\end{bmatrix}
=\frac{\rho}{\epsilon}\frac{{\Delta x}^2}{2}
\begin{bmatrix}
16 \\
15 \\
12 \\
7
\end{bmatrix} \notag
\end{equation}
ここで解析領域を区間 $[0,1]$ とすれば、$\Delta x=0.25$ スカラーポテンシャルの値は次のようになります。
\begin{equation}
\begin{bmatrix}
\phi^{1} \\
\phi^{2} \\
\phi^{3} \\
\phi^{4}
\end{bmatrix}
=\frac{\rho}{\epsilon}
\begin{bmatrix}
0.5 \\
0.46875 \\
0.375 \\
0.21875
\end{bmatrix} \notag
\end{equation}
この結果は解析的に求めた(1.1-10)式に一致します。
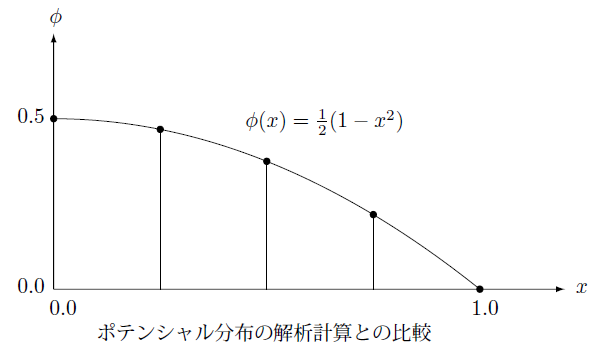
下の図は解析計算の結果と有限要素法による計算結果との比較です。有限要素法の結果は黒丸で示しています。
この結果は両者の結果が完全に一致していますが、通常は有限要素法の結果は数値計算に伴う誤差を含みます。
ここまでは静電場に関する方程式(1.1-6)式を1次元の場合に限って話をしてきましたが、現実の問題ではこのようなケースはまれで、2次元や3次元の問題を解く必要に迫られます。したがって次に2次元の問題について考えます。
