3次元の場合、静電場の方程式は(1.1-6)式となります。今後座標の記号 $(x,y,z)$ を $(x_1,x_2,x_3)$ とかくことにします。
そうすればこの式は次のようにかけます。
\begin{equation}
\sum_{i=1}^3\frac{\partial}{\partial x_i}\bigl(\epsilon\frac{\partial\phi}{\partial x_i}\bigr)=-\rho \tag*{$(1.4-1)$}
\end{equation}
1次元や2次元で行ったのと同様に、両辺に任意関数 $w(x_1,x_2,x_3)$ をかけて考えている領域 $V$ で積分します。
\begin{equation}
\int_Vw(x_1,x_2,x_3)\sum_{i=1}^3\frac{\partial}{\partial x_i}\bigl(\epsilon\frac{\partial\phi}{\partial x_i}\bigr)dV
=-\int_Vw(x_1,x_2,x_3)\rho dV \tag*{$(1.4-2)$}
\end{equation}
ここで、
\begin{equation}
\sum_{i=1}^3\frac{\partial}{\partial x_i}\bigl(w\epsilon\frac{\partial\phi}{\partial x_i}\bigr)
=\sum_{i=1}^3\frac{\partial w}{\partial x_i}\epsilon\frac{\partial\phi}{\partial x_i}
+w\sum_{i=1}^3\frac{\partial}{\partial x_i}\bigl(\epsilon\frac{\partial\phi}{\partial x_i}\bigr) \notag
\end{equation}
に注意すると、上の式の左辺は次のように変形できます。
\begin{equation}
\int_V\sum_{i=1}^3\frac{\partial}{\partial x_i}\bigl(w\epsilon\frac{\partial\phi}{\partial x_i}\bigr)dV
-\int_V\sum_{i=1}^3\frac{\partial w}{\partial x_i}\epsilon\frac{\partial\phi}{\partial x_i}dV \notag
\end{equation}
第一項はガウスの発散定理を使うと表面積分に変換できるので左辺は次のようになります。
\begin{equation}
\int_S\sum_{i=1}^3\bigl(w\epsilon\frac{\partial\phi}{\partial x_i}\bigr)n_idS
-\int_V\sum_{i=1}^3\frac{\partial w}{\partial x_i}\epsilon\frac{\partial\phi}{\partial x_i}dV \notag
\end{equation}
ここに $S$ は領域 $V$ の境界面で、$\boldsymbol{n}$ はこの境界面に外向きにとった単位法線ベクトルです。2次元問題のときに説明したとおり、境界条件として電場の法線成分がゼロであるようなノイマン境界条件の場合、ポテンシャルの法線方向の勾配がゼロになるのでこの積分はゼロとなります。
またポテンシャルの値が指定されているようなディレクレ境界条件の場合もこの項は考える必要がありません。
したがってここではこの項は省略します。
これより(1.4-2)式は次のようになります。
\begin{equation}
\int_V\sum_{i=1}^3\frac{\partial w}{\partial x_i}\epsilon\frac{\partial\phi}{\partial x_i}dV
=\int_Vw(x_1,x_2,x_3)\rho dV \tag*{$(1.4-3)$}
\end{equation}
領域 $V$ を有限要素分割した場合はこの積分は領域ごとの積分の和として表わすことが出来るので、
\begin{equation}
\sum_n\int_{V_n}\sum_{i=1}^3\frac{\partial w}{\partial x_i}\epsilon\frac{\partial\phi}{\partial x_i}dV
=\sum_n\int_{V_n}w(x_1,x_2,x_3)\rho dV \tag*{$(1.4-4)$}
\end{equation}
となります。ここに $V_n$ は $n$ 番目の要素領域です。
1次元や2次元のときにやったのと同じように要素内でのポテンシャルや任意関数 $w$ を次のように補間します。
\begin{equation}
\begin{split}
&\phi(\boldsymbol{x})=\sum_\alpha N_\alpha(\boldsymbol{x})\phi^\alpha \\
&w(\boldsymbol{x})=\sum_\alpha N_\alpha(\boldsymbol{x})w^\alpha
\end{split} \tag*{$(1.4-5)$}
\end{equation}
ここで $\boldsymbol{x}$ は座標 $(x_1,x_2,x_3)$ の位置ベクトルです。
ここから要素行列と要素ベクトルを作るのですが、基本的には1次元や2次元の場合と同じような手続きで行います。
ここで表現を少し変えます。
スカラー関数に作用する勾配ナブラ $\boldsymbol{\nabla}$ を使うと、
\begin{equation}
\begin{split}
&\frac{\partial w}{\partial x_i}=(\boldsymbol{\nabla}w)_i \\
&\epsilon\frac{\partial\phi}{\partial x_i}=\epsilon(\boldsymbol{\nabla}\phi)_i
\end{split} \notag
\end{equation}
とかけますが、これより(1.4-4)式の左辺の積分の中は次のようにかきかえることが出来ます。
\begin{equation}
\sum_{i=1}^3\frac{\partial w}{\partial x_i}\epsilon\frac{\partial\phi}{\partial x_i}
=\boldsymbol{\nabla}w\cdot\epsilon\boldsymbol{\nabla}\phi \notag
\end{equation}
この式に要素内で補間した任意関数 $w$ やポテンシャル(1.4-5)式を代入すると次のようになります。
\begin{equation}
\sum_\alpha\sum_\beta(\boldsymbol{\nabla}N_\alpha w^\alpha)\cdot(\epsilon\boldsymbol{\nabla}N_\beta\phi^\beta)
=\sum_\alpha\sum_\beta w^\alpha\bigl(\boldsymbol{\nabla}N_\alpha\cdot\epsilon\boldsymbol{\nabla}N_\beta\bigr)\phi^\beta \notag
\end{equation}
これを使うと $n$ 番目の要素の要素行列と要素ベクトルは、
\begin{equation}
\begin{split}
&K_{\alpha\beta}^{(n)}=\int_{V_n}\boldsymbol{\nabla}N_\alpha\cdot\epsilon\boldsymbol{\nabla}N_\beta dV \\
&F_\alpha^{(n)}=\int_{V_n}N_\alpha\rho dV
\end{split} \tag*{$(1.4-6)$}
\end{equation}
と表すことが出来ます。
要素行列と要素ベクトルから全体の係数行列とベクトルを作成する手順は2次元の場合詳しく説明しましたが、3次元の場合も全く同じです。
ここからは3次元の要素と補間関数について話します。
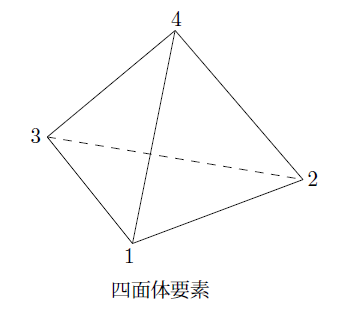
3次元の要素としてよく使われるのは四面体要素、五面体要素、そして六面体要素です。
四面体要素は2次元の三角形要素のように要素内を四つの節点の値から一次補間を行いますので一番基本的な要素と考えることが出来ます。
また、六面体要素は二次元の場合の四角形要素と同じようにアイソパラメトリック要素として使われることが多くその基本的な要素ということが出来ます。
まず、四面体要素から始めます。四面体要素は図に示したように四つの節点から構成されておりこの節点におけるポテンシャルの値などから要素内の点における値を一次補間します。
補間関数を求めるために要素内のポテンシャルを次のように一次関数で表します。
\begin{equation}
\phi(\boldsymbol{x})=ax+by+cz+d \notag
\end{equation}
この係数を求めるために4節点の座標を $(x_1,y_1,z_1)$、$(x_2,y_2,z_2)$、$(x_3,y_3,z_3)$、$(x_4,y_4,z_4)$ とし対応するポテンシャルの値を、$\phi^1$、$\phi^2$、$\phi^3$、$\phi^4$ とすれば上の式から次の係数に対する連立方程式が得られます。
\begin{equation}
\begin{bmatrix}
x_1 & y_1 & z_1 & 1 \\
x_2 & y_2 & z_2 & 1 \\
x_3 & y_3 & z_3 & 1 \\
x_4 & y_4 & z_4 & 1
\end{bmatrix}
\begin{bmatrix}
a \\
b \\
c \\
d
\end{bmatrix}
=
\begin{bmatrix}
\phi^1 \\
\phi^2 \\
\phi^3 \\
\phi^4
\end{bmatrix} \notag
\end{equation}
ここで左辺の行列の逆行列をクラーメルの公式を使って求めると次のようになります。
\begin{equation}
-\frac{1}{\Delta}
\begin{bmatrix}
h^1_x & h^2_x & h^3_x & h^4_x \\
h^1_y & h^2_y & h^3_y & h^4_y \\
h^1_z & h^2_z & h^3_z & h^4_z \\
-\Delta^1 & -\Delta^2 & -\Delta^3 & -\Delta^4
\end{bmatrix} \notag
\end{equation}
ここで、$\boldsymbol{h}^1$、$\boldsymbol{h}^2$、$\boldsymbol{h}^3$、$\boldsymbol{h}^4$ は、節点の位置ベクトル $\boldsymbol{x}^\alpha$ から作られる次のようなベクトルです。
\begin{equation}
\begin{split}
&\boldsymbol{h}^1=\boldsymbol{x}^2\times\boldsymbol{x}^3+\boldsymbol{x}^3\times\boldsymbol{x}^4+\boldsymbol{x}^4\times\boldsymbol{x}^2 \\
&\boldsymbol{h}^2=\boldsymbol{x}^1\times\boldsymbol{x}^4+\boldsymbol{x}^4\times\boldsymbol{x}^3+\boldsymbol{x}^3\times\boldsymbol{x}^1 \\
&\boldsymbol{h}^3=\boldsymbol{x}^1\times\boldsymbol{x}^2+\boldsymbol{x}^2\times\boldsymbol{x}^4+\boldsymbol{x}^4\times\boldsymbol{x}^1 \\
&\boldsymbol{h}^4=\boldsymbol{x}^1\times\boldsymbol{x}^3+\boldsymbol{x}^3\times\boldsymbol{x}^2+\boldsymbol{x}^2\times\boldsymbol{x}^1
\end{split} \notag
\end{equation}
また、
\begin{equation}
\begin{split}
&\Delta^1=\boldsymbol{x}^2\cdot[\boldsymbol{x}^3\times\boldsymbol{x}^4] \hspace{10mm} \Delta^2=\boldsymbol{x}^3\cdot[\boldsymbol{x}^1\times\boldsymbol{x}^4] \\
&\Delta^3=\boldsymbol{x}^4\cdot[\boldsymbol{x}^1\times\boldsymbol{x}^2] \hspace{10mm} \Delta^4=\boldsymbol{x}^1\cdot[\boldsymbol{x}^3\times\boldsymbol{x}^2]
\end{split} \notag
\end{equation}
であり、
\begin{equation}
\Delta=\Delta^1+\Delta^2+\Delta^3+\Delta^4 \notag
\end{equation}
は元の行列の行列式の符号を逆にしたものです。これより、係数 $a$、$b$、$c$、$d$ は次のようになります。
\begin{equation}
\begin{bmatrix}
a \\
b \\
c \\
d
\end{bmatrix}
=-\frac{1}{\Delta}
\begin{bmatrix}
h^1_x & h^2_x & h^3_x & h^4_x \\
h^1_y & h^2_y & h^3_y & h^4_y \\
h^1_z & h^2_z & h^3_z & h^4_z \\
-\Delta^1 & -\Delta^2 & -\Delta^3 & -\Delta^4
\end{bmatrix}
\begin{bmatrix}
\phi^1 \\
\phi^2 \\
\phi^3 \\
\phi^4
\end{bmatrix} \notag
\end{equation}
これより、
\begin{equation}
\begin{split}
\phi(\boldsymbol{x})&=
\begin{bmatrix}
x & y & z & 1
\end{bmatrix}
\begin{bmatrix}
a \\
b \\
c \\
d
\end{bmatrix} \\
&=-\frac{1}{\Delta}
\begin{bmatrix}
\boldsymbol{h}^1\cdot\boldsymbol{x}-\Delta^1 & \boldsymbol{h}^2\cdot\boldsymbol{x}-\Delta^2 & \boldsymbol{h}^3\cdot\boldsymbol{x}-\Delta^3 & \boldsymbol{h}^4\cdot\boldsymbol{x}-\Delta^4
\end{bmatrix}
\begin{bmatrix}
\phi^1 \\
\phi^2 \\
\phi^3 \\
\phi^4
\end{bmatrix} \notag
\end{split}
\end{equation}
となり、補間関数が次のように求まります。
\begin{equation}
\begin{split}
&N_1(\boldsymbol{x})=-\frac{1}{\Delta}(\boldsymbol{h}^1\cdot\boldsymbol{x}-\Delta^1) \\
&N_2(\boldsymbol{x})=-\frac{1}{\Delta}(\boldsymbol{h}^2\cdot\boldsymbol{x}-\Delta^2) \\
&N_3(\boldsymbol{x})=-\frac{1}{\Delta}(\boldsymbol{h}^3\cdot\boldsymbol{x}-\Delta^3) \\
&N_4(\boldsymbol{x})=-\frac{1}{\Delta}(\boldsymbol{h}^4\cdot\boldsymbol{x}-\Delta^4)
\end{split} \notag
\end{equation}
もう少し物理的な意味が取れるように辺ベクトル、
\begin{equation}
\begin{split}
&\boldsymbol{x}^{12}=\boldsymbol{x}^2-\boldsymbol{x}^1 \hspace{10mm} \boldsymbol{x}^{23}=\boldsymbol{x}^3-\boldsymbol{x}^2 \\
&\boldsymbol{x}^{13}=\boldsymbol{x}^3-\boldsymbol{x}^1 \hspace{10mm} \boldsymbol{x}^{14}=\boldsymbol{x}^4-\boldsymbol{x}^1 \\
&\boldsymbol{x}^{24}=\boldsymbol{x}^4-\boldsymbol{x}^2 \hspace{10mm} \boldsymbol{x}^{34}=\boldsymbol{x}^4-\boldsymbol{x}^3 \\
\end{split} \notag
\end{equation}
を使って変形すると次のようになります。
\begin{equation}
\begin{split}
&N_1(\boldsymbol{x})=\frac{1}{\Delta}[\boldsymbol{x}^{24}\times\boldsymbol{x}^{23}]\cdot(\boldsymbol{x}-\boldsymbol{x}^2) \\
&N_2(\boldsymbol{x})=\frac{1}{\Delta}[\boldsymbol{x}^{13}\times\boldsymbol{x}^{14}]\cdot(\boldsymbol{x}-\boldsymbol{x}^3) \\
&N_3(\boldsymbol{x})=\frac{1}{\Delta}[\boldsymbol{x}^{14}\times\boldsymbol{x}^{12}]\cdot(\boldsymbol{x}-\boldsymbol{x}^4) \\
&N_4(\boldsymbol{x})=\frac{1}{\Delta}[\boldsymbol{x}^{12}\times\boldsymbol{x}^{13}]\cdot(\boldsymbol{x}-\boldsymbol{x}^1)
\end{split} \tag*{$(1.4-7)$}
\end{equation}
またこのベクトルを使うと、
\begin{equation}
\Delta = [\boldsymbol{x}^{12}\times\boldsymbol{x}^{13}]\cdot\boldsymbol{x}^{14} \tag*{$(1.4-8)$}
\end{equation}
となりますが下の左の図から分かるように、これはこれらのベクトルを辺にもつ長方形の体積となります。したがって要素の体積 $V$ との関係は、
\begin{equation}
\Delta=6V \notag
\end{equation}
です。同様にして、(1.4-7)式の補間関数で例えば、
\begin{equation}
N_2(\boldsymbol{x})=\frac{1}{\Delta}[\boldsymbol{x}^{13}\times\boldsymbol{x}^{14}]\cdot(\boldsymbol{x}-\boldsymbol{x}^3) \notag
\end{equation}
の中の $[\boldsymbol{x}^{13}\times\boldsymbol{x}^{14}]\cdot(\boldsymbol{x}-\boldsymbol{x}^3)$ は右の図の太線で囲まれた四面体の体積 $V_2$ の6倍となります。
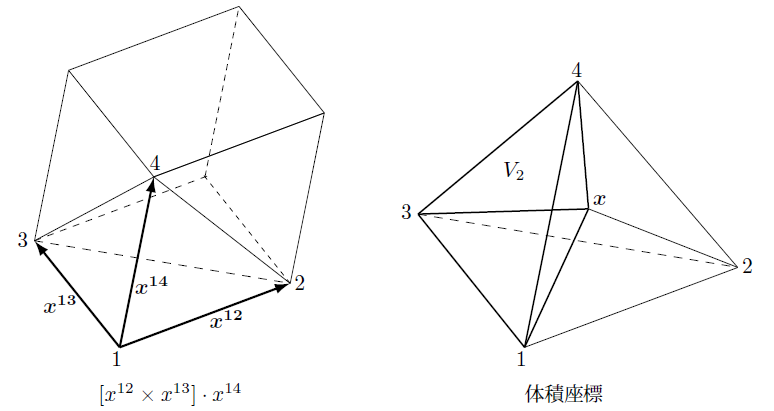
これより四面体要素の補間関数(1.4-7)式は次のようにかくことが出来ます。
\begin{equation}
\begin{split}
&N_1(\boldsymbol{x})=\frac{V_1}{V} \\
&N_2(\boldsymbol{x})=\frac{V_2}{V} \\
&N_3(\boldsymbol{x})=\frac{V_3}{V} \\
&N_4(\boldsymbol{x})=\frac{V_4}{V} \\
\end{split} \tag*{$(1.4-9)$}
\end{equation}
これは体積座標といい三角形要素の場合の面積座標に対応しており図形的にも分かりやすい表現になっています。
次に六面体要素について述べます。3次元の電場解析において六面体要素は精度向上のために重要な要素でよく使われています。2次元の場合の四角形要素のように3次元解析においても六面体要素は標準座標に変換して、その座標系における補間関数を使います。
下の図は、一般的な六面体要素の形状を示していますが、これを右の図のように一辺の長さが $2$ の頂点の座標が、$(\pm 1,\pm 1,\pm 1)$ の立方体になる座標系に変換します。
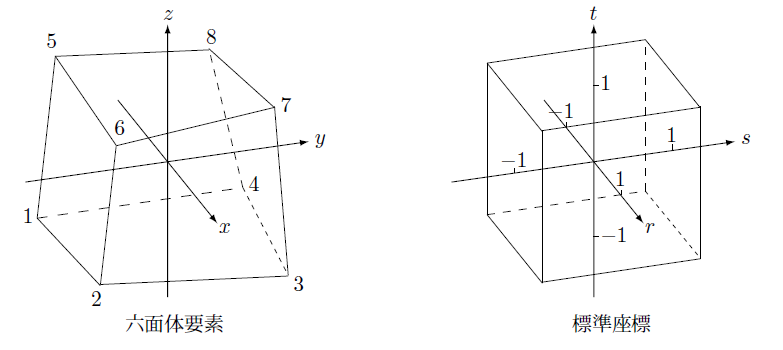
補間関数は次のようになります。
\begin{equation}
\begin{split}
&N_1(r,s,t)=\frac{1}{8}(1-r)(1-s)(1-t) \hspace{10mm} N_2(r,s,t)=\frac{1}{8}(1+r)(1-s)(1-t) \\
&N_3(r,s,t)=\frac{1}{8}(1+r)(1+s)(1-t) \hspace{10mm} N_4(r,s,t)=\frac{1}{8}(1-r)(1+s)(1-t) \\
&N_5(r,s,t)=\frac{1}{8}(1-r)(1-s)(1+t) \hspace{10mm} N_6(r,s,t)=\frac{1}{8}(1+r)(1-s)(1+t) \\
&N_7(r,s,t)=\frac{1}{8}(1+r)(1+s)(1+t) \hspace{10mm} N_8(r,s,t)=\frac{1}{8}(1-r)(1+s)(1+t)
\end{split} \tag*{$(1.4-10)$}
\end{equation}
アイソパラメトリック要素の場合、標準座標への変換は節点座標の座標を使って要素内部の座標をこの補間関数を使って補間します。
\begin{equation}
\begin{split}
&x=\sum_{\alpha=1}^8N_\alpha(r,s,t)x^\alpha \\
&y=\sum_{\alpha=1}^8N_\alpha(r,s,t)y^\alpha \\
&z=\sum_{\alpha=1}^8N_\alpha(r,s,t)z^\alpha
\end{split} \tag*{$(1.4-11)$}
\end{equation}
座標成分を系統的に扱うため座標 $(x,y,z)$ を $(x_1,x_2,x_3)$ とかいたように、標準座標 $(r,s,t)$ を $(\xi_1,\xi_2,\xi_3)$ とかきます。
\begin{equation}
x_i=\sum_\alpha N_\alpha(\boldsymbol{\xi})x_i^\alpha \tag*{$(1.4-12)$}
\end{equation}
ここで標準座標をベクトル $\boldsymbol{\xi}$ で表しています。
(1.4-6)式の要素行列を求めるには、この補間関数の勾配を求める必要がありますが、補間関数は標準座標の関数なので次のように変形します。
\begin{equation}
\frac{\partial N_\alpha(\boldsymbol{\xi})}{\partial x_i}=\sum_j\frac{\partial N_\alpha(\boldsymbol{\xi})}{\partial\xi_j}\frac{\partial\xi_j}{\partial x_i}
\tag*{$(1.4-13)$}
\end{equation}
ここで標準座標の微分を計算する必要があるのですが、次のように求めます。まず座標を標準座標で表した(1.4-12)式の両辺を標準座標で微分します。
\begin{equation}
\frac{\partial x_i}{\partial \xi_j}=\sum_\alpha\frac{\partial N_\alpha(\boldsymbol{\xi})}{\partial \xi_j}x_i^\alpha \tag*{$(1.4-14)$}
\end{equation}
ここで、
\begin{equation}
\frac{\partial x_i}{\partial x_j}=\sum_k\frac{\partial x_i}{\partial\xi_k}\frac{\partial\xi_k}{\partial x_j}=\delta_{ij} \notag
\end{equation}
ですが、これを行列でかけば次のようになります。
\begin{equation}
\begin{bmatrix}
\partial x_1/\partial\xi_1 & \partial x_1/\partial\xi_2 & \partial x_1/\partial\xi_3 \\
\partial x_2/\partial\xi_1 & \partial x_2/\partial\xi_2 & \partial x_2/\partial\xi_3 \\
\partial x_3/\partial\xi_1 & \partial x_3/\partial\xi_2 & \partial x_3/\partial\xi_3
\end{bmatrix}
\begin{bmatrix}
\partial\xi_1/\partial x_1 & \partial\xi_1/\partial x_2 & \partial\xi_1/\partial x_3 \\
\partial\xi_2/\partial x_1 & \partial\xi_2/\partial x_2 & \partial\xi_2/\partial x_3 \\
\partial\xi_3/\partial x_1 & \partial\xi_3/\partial x_2 & \partial\xi_3/\partial x_3
\end{bmatrix}
=
\begin{bmatrix}
1 & 0 & 0 \\
0 & 1 & 0 \\
0 & 0 & 1
\end{bmatrix} \notag
\end{equation}
これより、
\begin{equation}
\begin{bmatrix}
\partial\xi_1/\partial x_1 & \partial\xi_1/\partial x_2 & \partial\xi_1/\partial x_3 \\
\partial\xi_2/\partial x_1 & \partial\xi_2/\partial x_2 & \partial\xi_2/\partial x_3 \\
\partial\xi_3/\partial x_1 & \partial\xi_3/\partial x_2 & \partial\xi_3/\partial x_3
\end{bmatrix}
=\begin{bmatrix}
\partial x_1/\partial\xi_1 & \partial x_1/\partial\xi_2 & \partial x_1/\partial\xi_3 \\
\partial x_2/\partial\xi_1 & \partial x_2/\partial\xi_2 & \partial x_2/\partial\xi_3 \\
\partial x_3/\partial\xi_1 & \partial x_3/\partial\xi_2 & \partial x_3/\partial\xi_3
\end{bmatrix}^{-1} \notag
\end{equation}
となります。これより標準座標の微分 $\partial\xi_j/\partial x_i$ を求めることができます。
ここで変換行列の行列式を、
\begin{equation}
\Delta=det
\begin{bmatrix}
\partial x_1/\partial\xi_1 & \partial x_1/\partial\xi_2 & \partial x_1/\partial\xi_3 \\
\partial x_2/\partial\xi_1 & \partial x_2/\partial\xi_2 & \partial x_2/\partial\xi_3 \\
\partial x_3/\partial\xi_1 & \partial x_3/\partial\xi_2 & \partial x_3/\partial\xi_3
\end{bmatrix} \tag*{$(1.4-15)$}
\end{equation}
とおけば次のようになります。
\begin{equation}
\begin{split}
&\frac{\partial\xi_1}{\partial x_1}=\frac{1}{\Delta}\bigl(\frac{\partial x_2}{\partial\xi_2}\frac{\partial x_3}{\partial\xi_3}
-\frac{\partial x_3}{\partial\xi_2}\frac{\partial x_2}{\partial\xi_3}\bigr) \hspace{5mm}
\frac{\partial\xi_1}{\partial x_2}=\frac{1}{\Delta}\bigl(\frac{\partial x_3}{\partial\xi_2}\frac{\partial x_1}{\partial\xi_3}
-\frac{\partial x_1}{\partial\xi_2}\frac{\partial x_3}{\partial\xi_3}\bigr) \hspace{5mm}
\frac{\partial\xi_1}{\partial x_3}=\frac{1}{\Delta}\bigl(\frac{\partial x_2}{\partial\xi_3}\frac{\partial x_1}{\partial\xi_2}
-\frac{\partial x_1}{\partial\xi_3}\frac{\partial x_2}{\partial\xi_2}\bigr) \\
&\frac{\partial\xi_2}{\partial x_3}=\frac{1}{\Delta}\bigl(\frac{\partial x_3}{\partial\xi_1}\frac{\partial x_2}{\partial\xi_3}
-\frac{\partial x_2}{\partial\xi_1}\frac{\partial x_3}{\partial\xi_3}\bigr) \hspace{5mm}
\frac{\partial\xi_2}{\partial x_1}=\frac{1}{\Delta}\bigl(\frac{\partial x_1}{\partial\xi_1}\frac{\partial x_3}{\partial\xi_3}
-\frac{\partial x_3}{\partial\xi_1}\frac{\partial x_1}{\partial\xi_3}\bigr) \hspace{5mm}
\frac{\partial\xi_2}{\partial x_3}=\frac{1}{\Delta}\bigl(\frac{\partial x_1}{\partial\xi_3}\frac{\partial x_2}{\partial\xi_1}
-\frac{\partial x_2}{\partial\xi_3}\frac{\partial x_1}{\partial\xi_1}\bigr) \\
&\frac{\partial\xi_3}{\partial x_1}=\frac{1}{\Delta}\bigl(\frac{\partial x_2}{\partial\xi_1}\frac{\partial x_3}{\partial\xi_2}
-\frac{\partial x_3}{\partial\xi_1}\frac{\partial x_2}{\partial\xi_2}\bigr) \hspace{5mm}
\frac{\partial\xi_3}{\partial x_2}=\frac{1}{\Delta}\bigl(\frac{\partial x_1}{\partial\xi_2}\frac{\partial x_3}{\partial\xi_1}
-\frac{\partial x_3}{\partial\xi_2}\frac{\partial x_1}{\partial\xi_1}\bigr) \hspace{5mm}
\frac{\partial\xi_3}{\partial x_3}=\frac{1}{\Delta}\bigl(\frac{\partial x_1}{\partial\xi_1}\frac{\partial x_2}{\partial\xi_2}
-\frac{\partial x_2}{\partial\xi_1}\frac{\partial x_1}{\partial\xi_2}\bigr)
\end{split} \notag
\end{equation}
これを使って(1.4-13)式の補間関数の勾配を計算することができます。
これより要素行列と要素ベクトルは、
\begin{equation}
\begin{split}
K_{\alpha\beta}&=\iiint\sum_i\frac{\partial N_\alpha}{\partial x_i}\epsilon\frac{\partial N_\beta}{\partial x_i}dxdydz \\
&=\iiint\sum_i\frac{\partial N_\alpha}{\partial x_i}\epsilon\frac{\partial N_\beta}{\partial x_i}
\Bigl|\frac{\partial(x,y,z)}{\partial(r,s,t)}\Bigr|drdsdt \\
F_\alpha&=\iiint N_\alpha\rho\Bigl|\frac{\partial(x,y,z)}{\partial(r,s,t)}\Bigr|drdsdt
\end{split} \tag*{$(1.4-16)$}
\end{equation}
となります。ここにヤコビアンは、
\begin{equation}
\frac{\partial(x,y,z)}{\partial(r,s,t)}=\Delta \notag
\end{equation}
です。
これらの積分は2次元のところで説明したガウスの求積法によって次のように計算できます。
\begin{equation}
\begin{split}
&K_{\alpha\beta}=\sum_i\sum_j\sum_k\boldsymbol{\nabla}N_\alpha(r_i,s_j,t_k)\cdot\epsilon\boldsymbol{\nabla}N_\beta(r_i,s_j,t_k)
\Bigl|\frac{\partial(x,y,z)}{\partial(r,s,t)}\Bigr|_{(r_i,s_j,t_k)}w_{ijk} \\
&F_\alpha\sum_i\sum_j\sum_kN_\alpha(r_i,s_j,t_k)\rho\Bigl|\frac{\partial(x,y,z)}{\partial(r,s,t)}\Bigr|_{(r_i,s_j,t_k)}w_{ijk}
\end{split} \tag*{$(1.4-17)$}
\end{equation}
ここに、$w_{i,j,k}$ は積分点における重みです。
このようにしてすべての要素について要素行列と要素ベクトルが求まると、2次元の場合行ったように要素内のローカルな節点番号と対応するグローバルな節点番号の全体の係数行列とベクトルの要素に足しこむことによって連立方程式を作成することができます。
連立方程式が求まると、静電場に関する境界条件を適用します。
