1.現実の誘電体や磁性体に働く力
前に誘電体や磁性体を双極子の集合体として具体的な電磁力の計算を行いました。しかし現実の誘電体や磁性体が電磁場から受ける力は、マクロな電磁力以外の寄与も考える必要があります。流動性誘電体に関してはランダウ=リフシッツの教科書(1)に次の応力テンソルから計算できることが示されています。
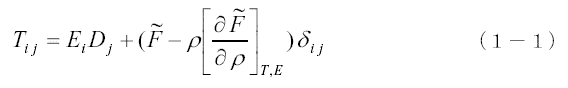
ここに
は誘電体の単位体積の熱力学ポテンシャルで単位体積の自由エネルギーF と、
の関係にあります。またρは誘電体の密度で微分は温度T と電場E を一定にして行います。
一方、誘電体を電気双極子の集合体とみなした場合の電磁応力テンソルは、

となります。
ここで、(1−1)式と(1−3)式を比較することによって誘電体の性質について議論したいと思います。
ここで取り扱う誘電体としては誘電率が温度と、密度のみの関数である線形誘電体を考えると、熱力学ポテンシャルは次のようになります。

F0は電場がないときの単位体積あたりの自由エネルギーです。この式を(1−1)式に代入すると次のようになります。
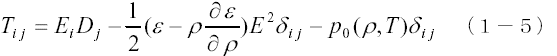
ただし、P0は、
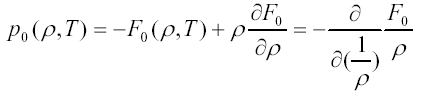
であり、電場が存在せず、密度と温度が与えられたときの媒質の圧力をあらわしています。
したがって、電磁力のみを問題とする場合(1−5)式は次のようになります。
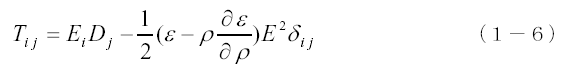
この式が(1−3)式と一致するためには次の関係が成立する必要があります。
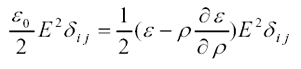

これを解くと、c を密度によらない定数として次の誘電率の密度依存性が求まります。

また電気分極Pをもとめると、
となり、誘電体を電気双極子の集合体とみなした場合は分極が密度と電場に比例することになります。
次に磁性体について考えます。流動性磁性体に関してはランダウ=リフシッツの教科書(1)
に次の応力テンソルから計算できることが示されています。
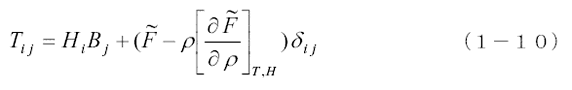
ここに
は磁性体の単位体積の熱力学ポテンシャルで単位体積の自由エネルギーF と、

の関係にあります。
一方、誘電体を磁気双極子の集合体とみなした場合の電磁応力テンソルは、
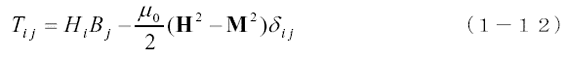
となります。ここで誘電体の場合と同様に、(1−10)式と(1−12)式を比較することによって磁性体の性質について議論したいと思います。
ここで取り扱う磁性体としては透磁率が温度と、密度のみの関数である線形磁性体を考えると、熱力学ポテンシャルは次のようになります。

F0は磁場がないときの単位体積あたりの自由エネルギーです。この式を(1−10)式に代入すると次のようになります。
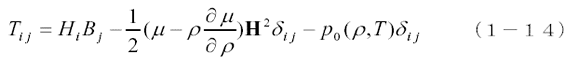
ただし、P0は電場のときと同様に磁場が存在せず、密度と温度が与えられたときの媒質の圧力です。したがって、電磁力のみを問題とする場合この式は次のようになります。
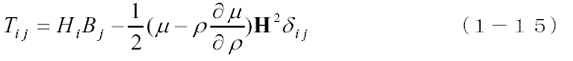
この式が(1−12)式と一致するためには次の関係が成立する必要があります。
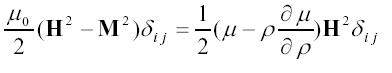
ところで、

ですから、これより、μ に間する次の微分方程式が得られます 。

変形すると、
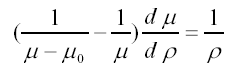
となるので、c を密度によらない定数として次のように透磁率の密度依存性が決まります。

これより磁化ベクトルMは、

となります。磁束密度であらわせば、
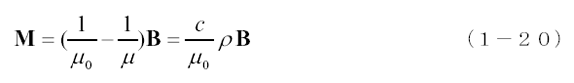
となり、磁性体を磁気双極子の集合体とみなした場合は磁化ベクトルが密度と磁束密度に比例することになります。
2.双極子によるモデル化と現実の物質
誘電体を電気双極子の集合体とした場合と、磁性体を磁気双極子の集合体としてあらわした場合、電気分極Pおよび磁化ベクトルMは(1−9)式、(1−20)式であらわされることが分かりました。改めてかくと、

です。この結果は電気双極子または磁気双極子が弱い電磁場の中であたかも気体分子のよう自由に運動しており互いに衝突しながら熱的に平衡な状態にあると考えれば納得のいくことです。この場合、分極や磁化が電場や磁束密度に比例することになり、また密度は単位体積中の双極子の数に比例しており分極や磁化がこれと比例します。
このことより双極子モデルによる電磁力は、物質が純粋にマクロな電磁場からの力のみを受けるとした場合の電磁力をあらわしているものと思われます。
もちろん現実の誘電体や磁性体ではこのようにマクロな電磁場からだけではなくミクロな電磁場による力も受けるために(2−1)式や(2−2)式は成立しません。
特別な例をもう一つあげます。これは流体が非圧縮性であり密度の変化がない場合です。このときは(1−6)式や(1−15)式の密度による微分項が消えるため応力テンソルはそれぞれ次のようになります。
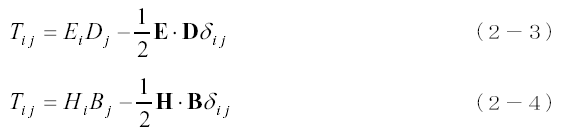
自由に動ける誘電性流体や磁性流体内部で電極や磁極をゆっくりと動かした場合は、ほぼ密度変化はないのでこれらの式によって電極や磁極に働く力が計算できます。
参考文献
(1)ランダウ=リフシッツ:理論物理学教程電磁気学1、東京図書株式会社(1982)
