さて、ベクトルポテンシャルによる方程式(5.1-6)式に有限要素法を適用するためにこれまでやってきたように両辺とベクトル関数 $\boldsymbol{w}$ の内積をとり、解析領域 $V$ で積分します。
\begin{equation}
\int_V\boldsymbol{w}\cdot\bigl(-\omega^2\epsilon\boldsymbol{A}+\mathrm{rot}\frac{1}{\mu}\mathrm{rot}\boldsymbol{A}\bigr)dV=\int_V\boldsymbol{w}\cdot\boldsymbol{J}dV \notag
\end{equation}
ここで左辺の積分に含まれる回転をとる項は部分積分によって次のように変形できます。
\begin{equation}
\int_V\boldsymbol{w}\cdot\mathrm{rot}\frac{1}{\mu}\mathrm{rot}\boldsymbol{A}dV
=\int_V\mathrm{rot}\boldsymbol{w}\cdot\frac{1}{\mu}\mathrm{rot}\boldsymbol{A}dV-\int_S\boldsymbol{w}\cdot[\boldsymbol{H}\times\boldsymbol{n}]dS \notag
\end{equation}
ここに右辺最後の積分は解析領域の境界面 $S$ での面積分であり、$\boldsymbol{n}$ はこの面に外向きにとった単位法線ベクトルです。
これより上の式は次のようになります。
\begin{equation}
-\omega^2\int_V\boldsymbol{w}\cdot\epsilon\boldsymbol{A}dV+\int_V\mathrm{rot}\boldsymbol{w}\cdot\frac{1}{\mu}\mathrm{rot}\boldsymbol{A}dV
=\int_V\boldsymbol{w}\cdot\boldsymbol{J}dV+\int_S\boldsymbol{w}\cdot[\boldsymbol{H}\times\boldsymbol{n}]dS \tag*{$(5.2-1)$}
\end{equation}
有限要素法では解析領域を要素分割しこの積分を要素ごとの積分の和におきかえます。要素の積分を行うさい要素内のベクトルポテンシャルなどは
補間関数を使って内挿し数値積分を実行します。
話を3次元に限定しているので辺要素の補間関数を用いて次のように補間します。
\begin{equation}
\begin{split}
&\boldsymbol{A}(\boldsymbol{x})=\sum_\alpha\boldsymbol{N}_\alpha(\boldsymbol{x})A^\alpha \\
&\boldsymbol{w}(\boldsymbol{x})=\sum_\alpha\boldsymbol{N}_\alpha(\boldsymbol{x})w^\alpha
\end{split} \tag*{$(5.2-2)$}
\end{equation}
ただし、$\alpha$ は要素内の辺番号です。
ここで $n$ 番目の要素に対して次の要素行列を作成します。
\begin{equation}
\begin{split}
&C_{\alpha\beta}^{(n)}=\int_{V_n}\boldsymbol{N}_\alpha\cdot\epsilon\boldsymbol{N}_\beta dV \\
&K_{\alpha\beta}^{(n)}=\int_{V_n}\mathrm{rot}\boldsymbol{N}_\alpha\cdot\frac{1}{\mu}\mathrm{rot}\boldsymbol{N}_\beta dV
\end{split} \tag*{$(5.2-3)$}
\end{equation}
また要素ベクトルとして、
\begin{equation}
F_\alpha=\int_{V_n}\boldsymbol{N}_\alpha\cdot\boldsymbol{J}dV+\int_{S_n}\boldsymbol{N}_\alpha\cdot[\boldsymbol{H}\times\boldsymbol{n}]dS \tag*{$(5.2-4)$}
\end{equation}
とします。この表面積分の項はこの要素が解析領域 $V$ の境界面 $S$ と接しているときだけに存在します。
これらの要素行列と要素ベクトルを解析領域全体で足しこんでやると有限要素法の連立方程式が次のように得られます。
\begin{equation}
(-\omega^2C+K)A=F \tag*{$(5.2-5)$}
\end{equation}
この方程式を与えられた境界条件により(5.2-4)式の境界積分を考慮して解けば周波数応答における電磁場を求めることが出来ます。
ところでこの積分は境界条件としてベクトルポテンシャルもしくは電場の接線成分が分かっていればディレクレ条件なのでこの境界積分はゼロになります。また、
\begin{equation}
[\boldsymbol{H}\times\boldsymbol{n}]=0 \notag
\end{equation}
をみたせばゼロとなります。
ところがこのような境界は特殊な場合で電波の入力ポートで電場の分布が分かっている場合や金属面のように表面で電場の接線成分がゼロとみなせる場合です。
低周波電磁場の場合は電磁場の発生源からある程度離れると減衰するのである程度距離をとって電場や磁場がゼロとするようなことが許されることもありますが、高周波電磁場は電波として伝搬するので適当な境界条件を付けるとそこで電波が反射して正しい結果を得ることが出来ません。
この境界積分を評価できれば良いのですが、解析した結果として決まる磁場 $\boldsymbol{H}$ を含んでいるのでこのままでは計算できません。
特別な場合としてこの境界を通して電磁波が通過しない場合と垂直に通過する場合について考えます。
電磁波の方向はポインティングベクトル、
\begin{equation}
\boldsymbol{P}=[\boldsymbol{E}\times\boldsymbol{H}] \tag*{$(5.2-6)$}
\end{equation}
の方向です。
まずこの面を電磁波が通過しない場合は、ポインティングベクトルの方向と境界面の法線方向が直交しています。
\begin{equation}
(\boldsymbol{P}\cdot\boldsymbol{n})=0 \notag
\end{equation}
このような境界は金属面などとの境界がある場合で、電場はこの境界面に対して垂直となります。
この境界条件を適用するには、要素のこの面を構成する辺のベクトルポテンシャルの射影成分、つまり電場のこの境界面内成分をゼロにする必要があります。
上の式の左辺を変形すると次のようになります。
\begin{equation}
([\boldsymbol{E}\times\boldsymbol{H}]\cdot\boldsymbol{n})=\boldsymbol{E}\cdot[\boldsymbol{H}\times\boldsymbol{n}]=0 \notag
\end{equation}
ここで電場の面内成分がゼロであればこの式は自動的にみたされることになります。
つぎに電磁波が境界面を垂直に通過する場合ですが、このときはポインティングベクトルの方向と境界面の法線方向とは一致しています。
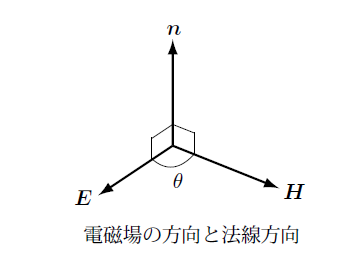
この図の $\theta$ は電場の方向と磁場の方向のなす角ですが平面波の場合は直角となります。ここでは境界面に垂直に通過する電磁波は平面波に近いものとします。
その場合 $[\boldsymbol{H}\times{n}]$ は図から分かりますように電場の方向を向き磁場の大きさを持ちます。
電場の大きさと磁場の大きさは電波インピーダンスを $Z$ とすれば、
\begin{equation}
|\boldsymbol{E}|=Z|\boldsymbol{H}| \tag*{$(5.2-7)$}
\end{equation}
の関係にあるので次のようにかくことが出来ます。
\begin{equation}
[\boldsymbol{H}\times\boldsymbol{n}]=\frac{1}{Z}\boldsymbol{E} \tag*{$(5.2-8)$}
\end{equation}
これより(5.2-4)式の表面積分項は次のようになります。
\begin{equation}
\int_{S_n}\boldsymbol{N}_\alpha\cdot\frac{1}{Z}\boldsymbol{E}dS=-j\omega\int_{S_n}\boldsymbol{N}_\alpha\cdot\frac{1}{Z}\boldsymbol{A}dS \notag
\end{equation}
これは未知であるベクトルポテンシャルを含んでいるので全体行列の方程式では左辺にもっていく必要があります。
そこで $n$ 番目の要素に対して次の要素行列を定義します。
\begin{equation}
L_{\alpha\beta}^{(n)}=\int_{V_n}\boldsymbol{N}_\alpha\cdot\frac{1}{Z}\boldsymbol{N}_\beta dV \tag*{$(5.2-9)$}
\end{equation}
これより全体の方程式は次のようになります。
\begin{equation}
(-\omega^2C+K+j\omega L)A=F \tag*{$(5.2-10)$}
\end{equation}
このように電磁波が通過する境界面をこのように扱う境界条件をインピーダンス境界条件とよんでいます。実際にはここで扱ったように境界面を通過する電磁波は平面波ではなく電場と磁場が必ずしも直交していませんし、境界面を垂直に通っていくとも限りません。
しかしある程度の距離をとって境界面を設定してやればこの境界条件が十分機能を果たすことが分かっています。
次に電磁場の駆動源を考えます。低周波の電磁場解析では電流や磁石が発生源となり、これらを入力することによって解析領域に発生する電磁場の解析を行いますが、高周波の場合外部から同軸ケーブルや導波管によって解析領域内に電磁波が入力されたり出力される場合が多くあります。
このような場合これら導波路の入力や出力面に境界条件として電場を与える必要があります。これらの面のことを今後ポートとよびます。
導波路内部では電磁波はこれに沿って一定方向に進むと考えられますのでこの方向と導波路の断面方向に分けて考えることにします。
また導波路では誘電率や透磁率を一定とすれば、高周波電磁場の方程式(5.1-6)式は、
\begin{equation}
-\omega^2\epsilon\boldsymbol{A}+\frac{1}{\mu}\mathrm{rot}\mathrm{rot}\boldsymbol{A}=0 \tag*{$(5.2-11)$}
\end{equation}
となります。ここで、
\begin{equation}
\mathrm{rot}\mathrm{rot}=\mathrm{grad}\mathrm{div}-\Delta \notag
\end{equation}
であることと、
\begin{equation}
\mathrm{div}\boldsymbol{A}=-\frac{1}{j\omega}\mathrm{div}\boldsymbol{E}=0 \notag
\end{equation}
に注意するとこの方程式は、
\begin{equation}
-\omega^2\epsilon\boldsymbol{A}-\frac{1}{\mu}\Delta\boldsymbol{A}=0 \notag
\end{equation}
となります。ここで導波路内部での電磁波の速度を、
\begin{equation}
c=\frac{1}{\sqrt{\epsilon\mu}} \tag*{$(5.2-12)$}
\end{equation}
とおけば上の式は少し変形して次のようにかけます。
\begin{equation}
\Delta\boldsymbol{A}=-\frac{\omega^2}{c^2}\boldsymbol{A} \tag*{$(5.2-13)$}
\end{equation}
ここで導波路の伝搬方向を $z$ 方向にとり断面方向を $xy$ 面とすれば、
\begin{equation}
\frac{\partial^2\boldsymbol{A}}{\partial x^2}+\frac{\partial^2\boldsymbol{A}}{\partial y^2}+\frac{\partial^2\boldsymbol{A}}{\partial z^2}=-\frac{\omega^2}{c^2}\boldsymbol{A} \notag
\end{equation}
となりますが、ベクトルポテンシャルを変数分離して、
\begin{equation}
\boldsymbol{A}(x,y,z)=\boldsymbol{A}_{xy}(x,y)e^{-jkz} \tag*{$(5.2-14)$}
\end{equation}
とおき、上の式に代入して変形すれば次のようになります。
\begin{equation}
\frac{\partial^2\boldsymbol{A}_{xy}}{\partial x^2}+\frac{\partial^2\boldsymbol{A}_{xy}}{\partial y^2}=-\bigl(\frac{\omega^2}{c^2}-k^2\bigr)\boldsymbol{A}_{xy} \tag*{$(5.2-15)$}
\end{equation}
電磁波の伝搬方向は電場と垂直方向なので同じ方向を持つベクトルポテンシャルもこの場合断面方向の成分しかもたないことになります。
この方程式は導波路の側面の境界条件が決まれば固有値方程式です。
したがって、電磁場の入力面の2次元有限要素法としてこの方程式を離散化すると一般固有値方程式となりますが、これを解いて固有値とそれに対応する固有ベクトルを求めることが出来ます。この固有ベクトルのことをモードとよぶことにします。
ここで2次元の有限要素法が出てきましたが、解析領域はすでに3次元の要素分割が行われているので、2次元の要素は3次元の要素の一つの面として自動的に作成することが出来ます。このように入力ポートにおける電場の入力はモードを指定することによって行うことが出来ます。
次に、解析結果から求まった電磁場からこの入力ポートや出力ポートにおけるインピーダンスなどの量をどのように計算するかについて述べます。
まず、出力結果からこれらポート面における電場や磁場が求まりますのでポインティングベクトルが(5.2-6)式より求めることが出来ます。
ポート面の解析領域から外向きにとった単位法線ベクトルを $\boldsymbol{n}$ とすれば、この面から単位時間あたりに入力する電磁エネルギーは次のようになります。
\begin{equation}
W=-\int_S[\boldsymbol{E}\times\boldsymbol{H}]\cdot\boldsymbol{n}dS \tag*{$(5.2-16)$}
\end{equation}
ここに $S$ はポート面です。電場と磁場は、
\begin{equation}
\begin{split}
&\boldsymbol{E}(t)=\boldsymbol{E}_R\mathrm{cos}\omega t-\boldsymbol{E}_I\mathrm{sin}\omega t \\
&\boldsymbol{H}(t)=\boldsymbol{H}_R\mathrm{cos}\omega t-\boldsymbol{H}_I\mathrm{sin}\omega t
\end{split} \notag
\end{equation}
これより、
\begin{equation}
\begin{split}
W=&-\int_S\bigl([\boldsymbol{E}_R\times\boldsymbol{H}_R]\cdot\mathrm{cos}^2\omega t+[\boldsymbol{E}_I\times\boldsymbol{H}_I]\cdot\mathrm{sin}^2\omega t \\
&+\int_S\bigl([\boldsymbol{E}_R\times\boldsymbol{H}_I]+[\boldsymbol{E}_I\times\boldsymbol{H}_R]\bigr)\cdot\boldsymbol{n}\mathrm{sin}\omega t\mathrm{cos}\omega tdS
\end{split} \notag
\end{equation}
となります。
一方このポートにはいる電流と電圧を、
\begin{equation}
\begin{split}
&v(t)=V_R\mathrm{cos}\omega t-V_I\mathrm{sin}\omega t \\
&i(t)=I_R\mathrm{cos}\omega t-I_I\mathrm{sin}\omega t
\end{split} \notag
\end{equation}
とすると、このポートから入る電磁エネルギーは、
\begin{equation}
\begin{split}
W&=vi=V_RI_R\mathrm{cos}^2\omega t+V_II_I\mathrm{sin}^2\omega t \\
&-(V_RI_I+V_II_R\bigr)\mathrm{sin}\omega t\mathrm{cos}\omega t
\end{split} \notag
\end{equation}
となります。これより電磁場で表した上の式と同じ時間変化をするものどうしを等しいとおけば次の関係が得られます。
\begin{equation}
\begin{split}
&V_RI_R=-\int_S[\boldsymbol{E}_R\times\boldsymbol{H}_R]\cdot\boldsymbol{n}dS \\
&V_II_I=-\int_S[\boldsymbol{E}_I\times\boldsymbol{H}_I]\cdot\boldsymbol{n}dS \\
&V_RI_I+V_II_R=-\int_S[\boldsymbol{E}_R\times\boldsymbol{H}_I]\cdot\boldsymbol{n}dS-\int_S[\boldsymbol{E}_I\times\boldsymbol{H}_R]\cdot\boldsymbol{n}dS
\end{split} \tag*{$(5.2-17)$}
\end{equation}
これよりポートに入力される電流が分かれば、ポートにおける電圧を次のように求めることが出来ます。
$I_R\ne 0$、$I_I\ne 0$ の場合
\begin{equation}
\begin{split}
&V_R=-\frac{1}{I_R}\int_S[\boldsymbol{E}_R\times\boldsymbol{H}_R]\cdot\boldsymbol{n}dS \\
&V_I=-\frac{1}{I_I}\int_S[\boldsymbol{E}_I\times\boldsymbol{H}_I]\cdot\boldsymbol{n}dS
\end{split} \tag*{$(5.2-18)$}
\end{equation}
$I_R=0$、$I_I\ne 0$ の場合
\begin{equation}
\begin{split}
&V_R=-\frac{1}{I_I}\Bigl(\int_S[\boldsymbol{E}_R\times\boldsymbol{H}_I]\cdot\boldsymbol{n}dS+\int_S[\boldsymbol{E}_I\times\boldsymbol{H}_R]\cdot\boldsymbol{n}dS\Bigr) \\
&V_I=-\frac{1}{I_I}\int_S[\boldsymbol{E}_I\times\boldsymbol{H}_I]\cdot\boldsymbol{n}dS
\end{split} \tag*{$(5.2-19)$}
\end{equation}
$I_R\ne 0$、$I_I=0$ の場合
\begin{equation}
\begin{split}
&V_R=-\frac{1}{I_R}\int_S[\boldsymbol{E}_R\times\boldsymbol{H}_R]\cdot\boldsymbol{n}dS \\
&V_I=-\frac{1}{I_R}\Bigl(\int_S[\boldsymbol{E}_R\times\boldsymbol{H}_I]\cdot\boldsymbol{n}dS+\int_S[\boldsymbol{E}_I\times\boldsymbol{H}_R]\cdot\boldsymbol{n}dS\Bigr)
\end{split} \tag*{$(5.2-20)$}
\end{equation}
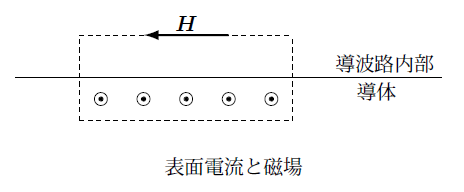
ここで導波路を流れる電流をどのように求めるかを考えます。導波路が金属で囲まれている場合は境界表面を電流が流れますが、この電流は下の図のようにそれを取り囲む破線で磁場 $\boldsymbol{H}$ を周回積分することによって求めることが出来ます。
ところが金属内は磁場がゼロなのでこの表面の磁場 $\boldsymbol{H}$ を面にそって積分すればよいことになります。
このポートにおけるインピーダンスは次のようになります。
\begin{equation}
Z=\frac{V_R+jV_I}{I_R+jI_I} \tag*{$(5.2-21)$}
\end{equation}
このように、電圧と電流で表せば伝送線を電気回路として扱うことが出来ます。

回路を流れる電流はポートから入ってきて図に示したように右の方に伝搬してこの回路の終端にある負荷 $Z_l$ で反射されます。
したがって、電流は右に進む前進波と反射して左に進む後進波との重ね合わせとなります。
\begin{equation}
I=\overrightarrow{I}-\overleftarrow{I} \tag*{$(5.2-22)$}
\end{equation}
電圧も次のようにかけます。
\begin{equation}
V=\overrightarrow{V}+\overleftarrow{V} \tag*{$(5.2-23)$}
\end{equation}
電流の場合は反対方向に流れるので両者の差になるのに対して電圧の場合は加算されます。
進行方向つまり $z$ 方向の変化はベクトルポテンシャルの変化が(5.2-14)式で表されるので次のように表すことが出来ます。
\begin{equation}
\begin{split}
&\overrightarrow{V}=Ae^{-jkz} \hspace{10mm} \overleftarrow{V}=Be^{jkz} \\
&\overrightarrow{I}=Ce^{-jkz} \hspace{10mm} \overleftarrow{I}=De^{jkz}
\end{split} \tag*{$(5.2-24)$}
\end{equation}
ところがこの回路の特性インピーダンスを $Z_0$ とすれば、
\begin{equation}
\begin{split}
&\frac{\overrightarrow{V}}{\overrightarrow{I}}=\frac{A}{C}=Z_0 \\
&\frac{\overleftarrow{V}}{\overleftarrow{I}}=\frac{B}{D}=Z_0
\end{split} \notag
\end{equation}
となります。これより電圧と電流を特性インピーダンスを使って表現すると次のようになります。
\begin{equation}
\begin{split}
&V=Ae^{-jkz}+Be^{jkz} \\
&I=\frac{A}{Z_0}e^{-jkz}-\frac{B}{Z_0}e^{jkz}
\end{split} \tag*{$(5.2-25)$}
\end{equation}
これよりこの回路の座標 $z$ におけるインピーダンスは次のようになります。
\begin{equation}
Z=\frac{V}{I}=\frac{Ae^{-jkz}+Be^{jkz}}{Ae^{-jkz}-Be^{jkz}}Z_0 \tag*{$(5.2-26)$}
\end{equation}
ここでポートの座標を $z=0$ とすればポートにおけるインピーダンスは、
\begin{equation}
Z=\frac{A+B}{A-B}Z_0 \notag
\end{equation}
となります。
ここで入射波と反射波の比である反射係数を、
\begin{equation}
\Gamma=\frac{B}{A} \notag
\end{equation}
とおけば上の式は次のようにかくことが出来ます。
\begin{equation}
Z=\frac{1+\Gamma}{1-\Gamma}Z_0 \notag
\end{equation}
この式を $\Gamma$ について解くと、
\begin{equation}
\Gamma=\frac{Z-Z_0}{Z+Z_0} \tag*{$(5.2-27)$}
\end{equation}
となります。
ここで解析領域が複数のポートを持つ場合を考えます。下の図は例としてポートの数が4個の場合を示しています。
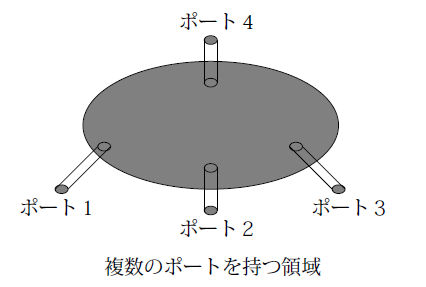
ここで $i$ 番目のポートの電流を $I_i$、電圧を $V_i$ としたとき、次のような量を定義します。
\begin{equation}
\begin{split}
&a_i=\frac{\overrightarrow{V_i}}{\sqrt{Z_0}}=\overrightarrow{I_i}\sqrt{Z_0} \\
&b_i=\frac{\overleftarrow{V_i}}{\sqrt{Z_0}}=\overleftarrow{I_i}\sqrt{Z_0}
\end{split} \tag*{$(5.2-28)$}
\end{equation}
入射波と反射波に分けた場合電流と電圧は特性インピーダンスの比だけが違うのでこのような量を導入すれば両者を統一的に扱うことが出来ます。
ここで $a_i$ は $i$ ポートから入射する波で、$b_i$ は $i$ ポートにおける反射波、つまり出ていく波を表しています。
ポート $i$ に関してこれを使うと電圧と電流は次のようにかけます。
\begin{equation}
\begin{split}
&V_i=\overrightarrow{V_i}+\overleftarrow{V_i}=\sqrt{Z_0}a_i+\sqrt{Z_0}b_i \\
&I_i=\overrightarrow{I_i}-\overleftarrow{I_i}=\frac{1}{\sqrt{Z_0}}a_i-\frac{1}{\sqrt{Z_0}}b_i
\end{split} \notag
\end{equation}
これは $a_i$ と $b_i$ についての連立方程式とみなすことが出来ます。そこでこの方程式を解くと次の式が得られます。
\begin{equation}
\begin{split}
&a_i=\frac{1}{2\sqrt{Z_0}}(V_i+Z_0I_i) \\
&b_i=\frac{1}{2\sqrt{Z_0}}(V_i-Z_0I_i)
\end{split} \tag*{$(5.2-29)$}
\end{equation}
ここで、$i$ ポートから $a_i$ の入射波があったとき $j$ ポートから出ていく波 $b_j$ を次のように表すことが出来ます。
\begin{equation}
b_j=\sum_iS_{ji}a_i \tag*{$(5.2-30)$}
\end{equation}
この行列 $S$ は散乱行列とよび、この要素 $S_{ij}$ のことを $S$ パラメータとよんでいます。
入力ポートが一つで $i$ 番目のポートとします。このとき他のポートは特性インピーダンスに整合され反射がないとすれば、
\begin{equation}
a_j=0 \hspace{5mm} (j\ne i) \notag
\end{equation}
なので、$S$ パラメータは次のように表されます。
\begin{equation}
S_{ji}=\frac{b_j}{a_i} \tag*{$(5.2-31)$}
\end{equation}
技術情報 Techinicalinfo
- ホーム
- 技術情報
- 【技術情報】有限要素法入門
- 5.2 有限要素法
【技術情報】有限要素法入門
