ここでいう2次元とは磁場や磁束密度が考えている面すなわち $xy$ 面方向の成分しか持たず、この面に垂直な $z$ 成分を持たないときです。
またこの面に垂直な方向で場は変化しません。
このような場合、磁束密度をベクトルポテンシャルで表すと次のようになります。
\begin{equation}
\begin{split}
&B_x=\frac{\partial A_z}{\partial y}-\frac{\partial A_y}{\partial z}=\frac{\partial A_z}{\partial y} \\
&B_y=\frac{\partial A_x}{\partial z}-\frac{\partial A_z}{\partial x}=-\frac{\partial A_z}{\partial x} \\
&B_z=\frac{\partial A_y}{\partial x}-\frac{\partial A_x}{\partial y}=0
\end{split} \tag*{$(2.2-1)$}
\end{equation}
これより、(2.1-5)式の左辺は、
\begin{equation}
\begin{split}
&(\mathrm{rot}\frac{1}{\mu}\boldsymbol{B})_x=\frac{\partial}{\partial y}\bigl(\frac{1}{\mu}B_z\bigr)-\frac{\partial}{\partial z}\bigl(\frac{1}{\mu}B_y\bigr)=0 \\
&(\mathrm{rot}\frac{1}{\mu}\boldsymbol{B})_y=\frac{\partial}{\partial z}\bigl(\frac{1}{\mu}B_x\bigr)-\frac{\partial}{\partial x}\bigl(\frac{1}{\mu}B_z\bigr)=0 \\
&(\mathrm{rot}\frac{1}{\mu}\boldsymbol{B})_z=\frac{\partial}{\partial x}\bigl(\frac{1}{\mu}B_y\bigr)-\frac{\partial}{\partial y}\bigl(\frac{1}{\mu}B_x\bigr)
=-\frac{\partial}{\partial x}\bigl(\frac{1}{\mu}\frac{\partial A_z}{\partial x}\bigr)
-\frac{\partial}{\partial y}\bigl(\frac{1}{\mu}\frac{\partial A_z}{\partial y}\bigr)
\end{split} \notag
\end{equation}
となります。これより2次元の基礎方程式は次のようにかくことが出来ます。
\begin{equation}
\frac{\partial}{\partial x}\bigl(\frac{1}{\mu}\frac{\partial A_z}{\partial x}\bigr)
+\frac{\partial}{\partial y}\bigl(\frac{1}{\mu}\frac{\partial A_z}{\partial y}\bigr)=-J_z \tag*{$(2.2-2)$}
\end{equation}
この式は静電場の2次元の場合の方程式(1.3-1)式に対応します。この方程式の両辺に任意関数 $w(x,y)$ をかけて解析領域 $S$ で積分します。
\begin{equation}
\int_Sw(x,y)\bigl[\frac{\partial}{\partial x}\bigl(\frac{1}{\mu}\frac{\partial A_z}{\partial x}\bigr)
+\frac{\partial}{\partial y}\bigl(\frac{1}{\mu}\frac{\partial A_z}{\partial y}\bigr)\bigr]dS=-\int_Sw(x,y)J_z dS \tag*{$(2.2-3)$}
\end{equation}
この式の左辺は部分積分とガウスの発散定理を使うと次のように変形できます。
\begin{equation}
\begin{split}
&\int_S\bigl[\frac{\partial}{\partial x}\bigl(w(x,y)\frac{1}{\mu}\frac{\partial A_z}{\partial x}\bigr)
+\frac{\partial}{\partial y}\bigl(w(x,y)\frac{1}{\mu}\frac{\partial A_z}{\partial y}\bigr)\bigr]dS
-\int_S\bigl[\frac{\partial w}{\partial x}\frac{1}{\mu}\frac{\partial A_z}{\partial x}
+\frac{\partial w}{\partial y}\frac{1}{\mu}\frac{\partial A_z}{\partial y}\bigr]dS \\
&=\oint\bigl[\bigl(w(x,y)\frac{1}{\mu}\frac{\partial A_z}{\partial x}\bigr)n_x
+\bigl(w(x,y)\frac{1}{\mu}\frac{\partial A_z}{\partial y}\bigr)n_y\bigr]dl
-\int_S\bigl[\frac{\partial w}{\partial x}\frac{1}{\mu}\frac{\partial A_z}{\partial x}
+\frac{\partial w}{\partial y}\frac{1}{\mu}\frac{\partial A_z}{\partial y}\bigr]dS \\
&=\oint w(x,y)[\boldsymbol{H}\times\boldsymbol{n}]_zdl
-\int_S\bigl(\frac{\partial w}{\partial x}\frac{1}{\mu}\frac{\partial A_z}{\partial x}
+\frac{\partial w}{\partial y}\frac{1}{\mu}\frac{\partial A_z}{\partial y}\bigr)dS
\end{split} \notag
\end{equation}
これより(2.2-3)式は次のようになります。
\begin{equation}
\int_S\bigl(\frac{\partial w}{\partial x}\frac{1}{\mu}\frac{\partial A_z}{\partial x}
+\frac{\partial w}{\partial y}\frac{1}{\mu}\frac{\partial A_z}{\partial y}\bigr)dS
=\int_Sw(x,y)J_z dS+\oint w(x,y)[\boldsymbol{H}\times\boldsymbol{n}]_zdl \tag*{$(2.2-4)$}
\end{equation}
この方程式を見るとノイマン境界条件は磁場 $\boldsymbol{H}$ が境界線の法線方向を向いている場合はゼロになることを示しています。
この境界条件は自然境界条件ともよばれており例を下の図に示します。
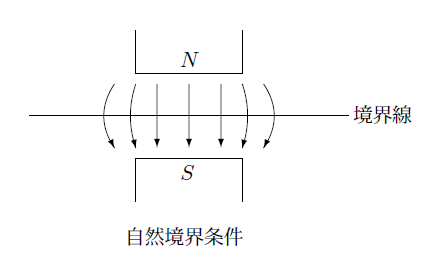
この例のように境界線をはさんで対称な位置に同じ形の磁石があり、上の磁石は下面に $N$ 極、下の磁石は上面に $S$ 極がある場合、磁場は境界線に垂直になります。
さてここからは解析領域 $S$ を有限要素に分割し、要素内でベクトルポテンシャルの $z$ 成分と関数 $w$ を次のように補間します。
\begin{equation}
\begin{split}
&A_z(x,y)=\sum_\alpha N_\alpha(r,s)A_z^\alpha \\
&w(x,y)=\sum_\alpha N_\alpha(r,s)w^\alpha
\end{split} \tag*{$(2.2-5)$}
\end{equation}
ここでの補間関数は静電場解析の2次元のときに説明した節点要素におけるもので、三角形要素の場合は(1.3-15)式、四角形要素のアイソパラメトリック要素の場合は(1.3-28)式となります。
これらの補間関数を使うと要素行列と要素ベクトルは次のようになります。
\begin{equation}
\begin{split}
&K_{\alpha\beta}^{(n)}=\int_{S_n}\bigl(\frac{\partial N_\alpha}{\partial x}\frac{1}{\mu}\frac{\partial N_\beta}{\partial x}
+\frac{\partial N_\alpha}{\partial y}\frac{1}{\mu}\frac{\partial N_\beta}{\partial y}\bigr)dS \\
&F_\alpha^{(n)}=\int_{S_n}N_\alpha J_z dS+\int_{l_n}N_\alpha[\boldsymbol{H}\times\boldsymbol{n}]_zdl
\end{split} \tag*{$(2.2-6)$}
\end{equation}
ただし要素ベクトルの右辺第2項は自然境界がこの要素に含まれる場合のもので積分はその境界線 $l_n$ について行います。
技術情報 Techinicalinfo
- ホーム
- 技術情報
- 【技術情報】有限要素法入門
- 2.2 2次元問題
【技術情報】有限要素法入門
