第5回 境界条件
前回は有限領域で解析するために生じる外側の境界、また対称性を利用して解析領域を狭くしたときに生じる内部(断面)の境界をご紹介致しました。
これらの境界には境界条件を設定する必要があります。
境界条件はいくつか種類がありますが、磁場解析では代表的な2種類の境界条件をご紹介致します。
●対称境界条件
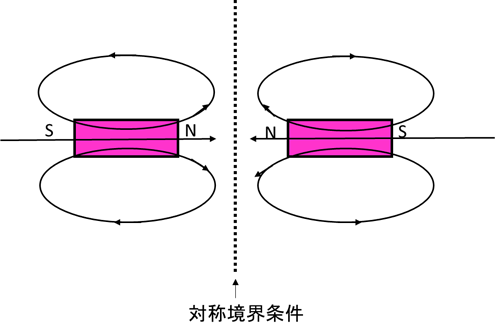
図5−1.対称境界条件
対称境界条件は境界(図5−1の点線)において、磁場が境界と“平行”になる境界条件です。
図5−1では例として磁石を考えていますが、N極が対向していますので、境界では境界と平行な磁場になります。
●反対称境界条件
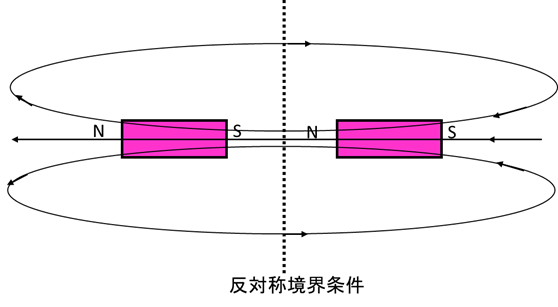
図5−2.反対称境界条件
反対称境界条件は境界(図5−2の点線)において、磁場が境界と“垂直”になる境界条件です。
今度は磁石のS極とN極が対向していますので、境界における磁場は境界と垂直になっています。
前回、対称性を利用したモデルの簡略化において、新たに出現した境界についてご紹介致しました。(図4−6)
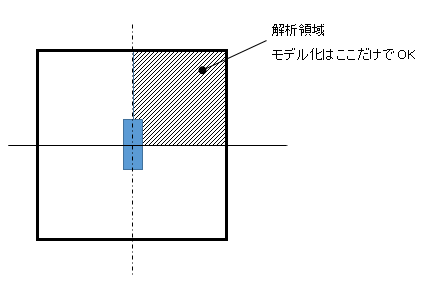
図4−6.4分の1モデル(再掲)
この場合、解析領域は、図4−6の斜線の領域になります。この斜線部を改めて、図5−3に示します。
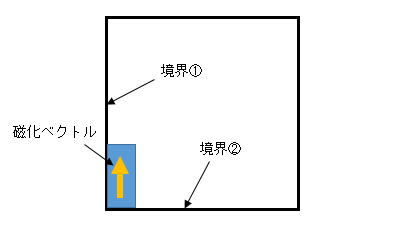
図5−3.解析領域
磁化ベクトルの向きから、境界の磁場の向きを予想できます。
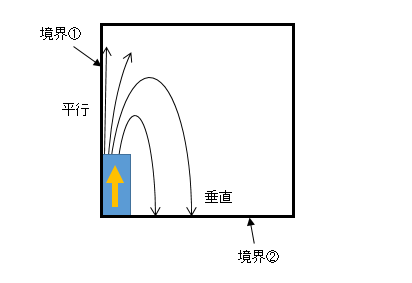
図5−4.磁場の向きの予想
磁場が境界に対して、平行であれば、対称境界条件、垂直であれば、反対称境界条件の関係を用いて考えます。
図5−4より磁場の向きは境界@で平行、境界Aで垂直と予想できますので、境界@は対称境界条件、境界Aは反対称境界条件となります。
●数値実験
実際に境界条件に着目した数値実験を行い、確認したいと思います。簡単のため、図5−5に示すような2次元の電磁石を考えます。
図5−5は1分の1モデルです。
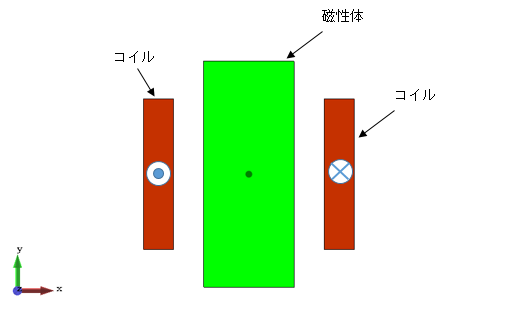
図5−5.解析概要図
図5−6に1分の1モデルの磁束密度ベクトル図を示します。

図5−6.磁束密度[T] 1分の1モデル
次にYZ面に対して、2分の1モデルを考えます。境界@では磁場が平行になりますので、対称境界条件を設定します。
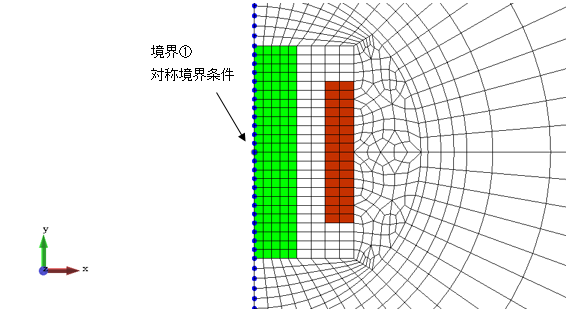
図5−7.2分の1モデル
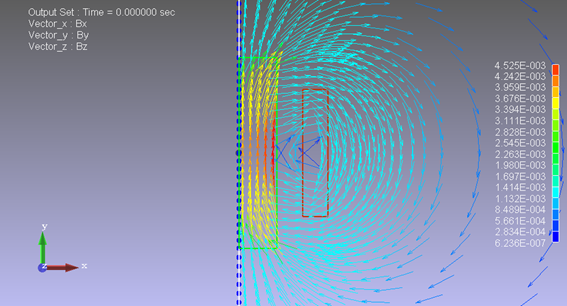
図5−8.磁束密度[T] 2分の1モデル
境界@において、境界に平行な磁束密度が見られ、妥当な結果と考えられます。ここで、境界@に反対称境界条件を設定してみます。
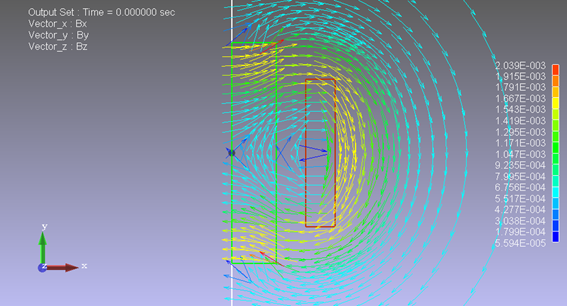
図5−9.磁束密度[T] 2分の1モデル 反対称境界条件
境界@に対して垂直の磁束密度ベクトルが得られます。図5−5の電流の向きの場合、想定した磁場の向きとは異なり、不適切な境界条件となります。
正しい境界条件が設定されているかどうか、ベクトル図を表示させて確認することが重要となります。
最後に4分の1モデルについて、境界@に対称境界条件、境界Aに反対称境界条件を設定した解析結果をご紹介致します。
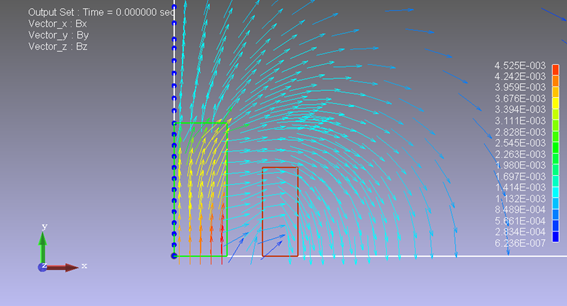
図5−10.磁束密度[T] 4分の1モデル
今回、ご紹介致しました境界条件の設定法はそのまま3次元解析でも有効です。
●ポイント
境界に対して、磁場が平行のとき:対称境界条件
境界に対して、磁場が垂直のとき:反対称境界条件
ご意見・ご感想は
こちらから->
