有限要素法で解析しようとする対象が地磁気や空芯コイルの作る磁場の中に置かれている場合はこのような外から受ける電磁場、すなわち外場を考慮した計算が必要になります。この節ではこのような場合の計算方法について述べます。
まず、低周波磁場の場合についてですが、基礎方程式は(4.1-8)式です。磁場から磁化の項を除き右辺に移動すると次の式となります。
\begin{equation}
\sigma\frac{\partial\boldsymbol{A}}{\partial t}+\mathrm{rot}\frac{1}{\mu_0}\mathrm{rot}\boldsymbol{A}=\boldsymbol{J}+\mathrm{rot}\boldsymbol{M}+\boldsymbol{J}_0 \tag*{$(6.3-1)$}
\end{equation}
また右辺の $\boldsymbol{J}_0$ は外場を発生させている電流であり、発生源が永久磁石の場合は磁化電流を表していると考えます。
外場を作っている発生源が単独で存在している場合はこの電流は次のようなベクトルポテンシャル $\boldsymbol{A}_0$ を発生させます。
\begin{equation}
\mathrm{rot}\frac{1}{\mu_0}\mathrm{rot}\boldsymbol{A}_0=\boldsymbol{J}_0 \tag*{$(6.3-2)$}
\end{equation}
電磁場には重ね合わせの原理が成り立ちますので、いろんな発生源があるときの場は、それぞれが単独にある場合の場を足し合わせることによって求めることが出来ます。
そこで今求めようとしているベクトルポテンシャル $\boldsymbol{A}$ も外場がないときのベクトルポテンシャル $\boldsymbol{A}_1$ と外場による $\boldsymbol{A}_0$ の和と考えることが出来ます。
\begin{equation}
\boldsymbol{A}=\boldsymbol{A}_0+\boldsymbol{A}_1 \tag*{$(6.3-3)$}
\end{equation}
これらの式を(6.3-1)式に代入すると次のようになります。
\begin{equation}
\sigma\frac{\partial}{\partial t}(\boldsymbol{A}_0+\boldsymbol{A}_1)+\mathrm{rot}\frac{1}{\mu_0}\mathrm{rot}(\boldsymbol{A}_0+\boldsymbol{A}_1)
=\boldsymbol{J}+\mathrm{rot}\boldsymbol{M}+\mathrm{rot}\frac{1}{\mu_0}\mathrm{rot}\boldsymbol{A}_0 \notag
\end{equation}
変形すると次のようになります。
\begin{equation}
\sigma\frac{\partial\boldsymbol{A}_1}{\partial t}+\mathrm{rot}\frac{1}{\mu_0}\mathrm{rot}\boldsymbol{A}_1
=\boldsymbol{J}+\mathrm{rot}\boldsymbol{M}-\sigma\frac{\partial\boldsymbol{A}_0}{\partial t} \tag*{$(6.3-4)$}
\end{equation}
ここで右辺の外場によるベクトルポテンシャルは分かっているのでこの方程式を $\boldsymbol{A}_1$ について解けばよいのですが、右辺の磁化 $\boldsymbol{M}$ をどう扱うかが問題です。
磁性体が線形の場合は、
\begin{equation}
\boldsymbol{M}=\frac{1}{\mu_0}\boldsymbol{B}-\boldsymbol{H}=\bigl(\frac{1}{\mu_0}-\frac{1}{\mu}\bigr)(\mathrm{rot}\boldsymbol{A}_0+\mathrm{rot}\boldsymbol{A}_1) \notag
\end{equation}
となるのでこれを上の式に代入して少し変形すれば次のようになります。
\begin{equation}
\sigma\frac{\partial\boldsymbol{A}_1}{\partial t}+\mathrm{rot}\frac{1}{\mu}\mathrm{rot}\boldsymbol{A}_1
=\boldsymbol{J}-\sigma\frac{\partial\boldsymbol{A}_0}{\partial t}+\mathrm{rot}\bigl(\frac{1}{\mu_0}-\frac{1}{\mu}\bigr)\mathrm{rot}\boldsymbol{A}_0 \tag*{$(6.3-5)$}
\end{equation}
この式は右辺がすべてわかっている量で表されているので解くことが出来ます。解いた結果求まった $\boldsymbol{A}_1$ を(6.3-3)に代入することによって外場を含めた電磁場を求めることが出来ます。
次に非線形の場合ですが、非線形の磁性体の磁化は外場を含めた磁束密度、
\begin{equation}
\boldsymbol{B}=\boldsymbol{B}_0+\boldsymbol{B}_1=\mathrm{rot}\boldsymbol{A}_0+\mathrm{rot}\boldsymbol{A}_1 \notag
\end{equation}
の関数として次のように表されます。
\begin{equation}
\boldsymbol{M}=\boldsymbol{M}(\boldsymbol{B}_0+\boldsymbol{B}_1) \tag*{$(6.3-6)$}
\end{equation}
方程式(6.3-4)式を非線形方程式として解く場合は第3章の2節でも述べたようにニュートン・ラプソン法で解く必要があります。
この場合ベクトルポテンシャル $\boldsymbol{A}_1$ を未知として解くのでその修正分を $\Delta\boldsymbol{A}_1$ とかくと次の式を繰り返し解くことになります。
\begin{equation}
\begin{split}
\sigma\frac{\partial\Delta\boldsymbol{A}_1}{\partial t}+\mathrm{rot}\frac{1}{\mu_0}\mathrm{rot}\Delta\boldsymbol{A}_1
-\mathrm{rot}\frac{\partial\boldsymbol{M}}{\partial\boldsymbol{B}}\mathrm{rot}\Delta\boldsymbol{A}_1
&=\boldsymbol{J}+\mathrm{rot}\boldsymbol{M}-\sigma\frac{\partial\boldsymbol{A}_0}{\partial t} \\
&-\sigma\frac{\partial\boldsymbol{A}_1}{\partial t}-\mathrm{rot}\frac{1}{\mu_0}\mathrm{rot}\boldsymbol{A}_1
\end{split} \tag*{$(6.3-7)$}
\end{equation}
この右辺の磁化 $\boldsymbol{M}$ は繰り返しの途中に求まった磁束密度を使って(6.3-6)式の計算を行い求めていきます。
ここでは時間の離散化について述べませんが、以前使った方法をこの場合についてもそのまま適用することが出来ます。また、$\boldsymbol{A}-\phi$ 法についても同様に行うことが出来ます。
次に高周波の場合についてですが、基礎方程式は(5.1-6)式です。
\begin{equation}
-\omega^2\epsilon\boldsymbol{A}+\mathrm{rot}\frac{1}{\mu}\mathrm{rot}\boldsymbol{A}=\boldsymbol{J} \notag
\end{equation}
高周波については周波数応答解析として扱っていますので誘電率や透磁率は線形として扱っています。
これに外場の発生源として右辺に $\boldsymbol{J}_0$ を加えると次のようになります。
\begin{equation}
-\omega^2\epsilon\boldsymbol{A}+\mathrm{rot}\frac{1}{\mu}\mathrm{rot}\boldsymbol{A}=\boldsymbol{J}+\boldsymbol{J}_0 \tag*{$(6.3-8)$}
\end{equation}
外場に関する方程式は、
\begin{equation}
-\omega^2\epsilon_0\boldsymbol{A}_0+\mathrm{rot}\frac{1}{\mu_0}\mathrm{rot}\boldsymbol{A}_0=\boldsymbol{J}_0 \tag*{$(6.3-9)$}
\end{equation}
です。低周波の場合の(6.3-3)式のようにベクトルポテンシャルを外場によるものとそれ以外の部分に分けて(6.3-8)式に代入すると
次のようになります。
\begin{equation}
-\omega^2\epsilon(\boldsymbol{A}_0+\boldsymbol{A}_1)+\mathrm{rot}\frac{1}{\mu}\mathrm{rot}(\boldsymbol{A}_0+\boldsymbol{A}_1)
=\boldsymbol{J}-\omega^2\epsilon_0\boldsymbol{A}_0+\mathrm{rot}\frac{1}{\mu_0}\mathrm{rot}\boldsymbol{A}_0 \notag
\end{equation}
未知数を左辺にもっていくように変形すると次のようになります。
\begin{equation}
-\omega^2\epsilon\boldsymbol{A}_1+\mathrm{rot}\frac{1}{\mu}\mathrm{rot}\boldsymbol{A}_1
=\boldsymbol{J}-\omega^2(\epsilon_0-\epsilon)\boldsymbol{A}_0+\mathrm{rot}\bigl(\frac{1}{\mu_0}-\frac{1}{\mu}\bigr)\mathrm{rot}\boldsymbol{A}_0 \tag*{$(6.3-10)$}
\end{equation}
この右辺は外場としてわかっている量なのでこの方程式は解くことが出来ます。その結果得られた $\boldsymbol{A}_1$ から(6.3-3)式により電磁場を求めることが出来ます。
高周波解析の場合は、遠方から来る平面波に対する散乱などが問題になる場合が結構あります。このような時は入射波として平面波を外場として、
\begin{equation}
\boldsymbol{A}_0(\boldsymbol{x},t)=\frac{1}{-j\omega}\boldsymbol{E}_0e^{(-\boldsymbol{k}\cdot\boldsymbol{x}+\omega t)} \notag
\end{equation}
などとしてこの方法を使います。ここに $\boldsymbol{k}$ は波数ベクトルとよばれるもので平面波の進行方向のベクトルです。
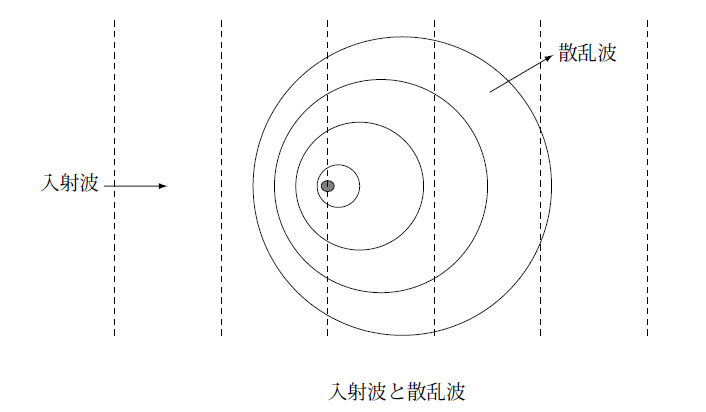
この図は中央にある散乱体によって左から来た平面波が散乱した様子を表しています。
このような例は外場と散乱波についてかなり直感的に理解することが出来ますが、次の図に示すような屈折の問題はどうでしょうか。
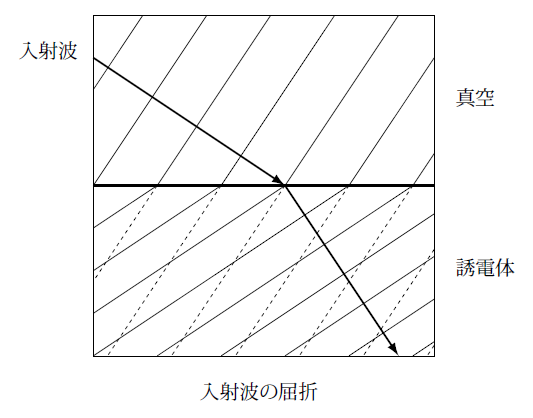
真空から入射した電磁波が誘電体で屈折して方向を変える場合です。図では入射波と屈折波の波面を実線で示しています。
実際には反射波もありますが今問題にしていませんので図では省略しています。
このとき外場としては真空中の平面電磁波を考えるのですが、これは真空領域だけではなく誘電体の領域にも図の破線で示しているように存在します。
合成波としては図に示した実線だけになるはずですからこの破線で表されている波は散乱波がちょうど打ち消すように働かなくてはなりません。
このようなことが可能なのか疑問に思いますが、実際にこの方法で解析すると正しい答えが得られます。
