1.マックスウェルの応力と磁性体に働く力
誘電体の場合と同様に、磁性体全体が磁場から受ける力はマックスウェルの応力によって計算できることが知られています。磁場に関するマックスウェルの応力は、磁束密度Bの成分と真空の透磁率μ0を使って次のように書くことができます。
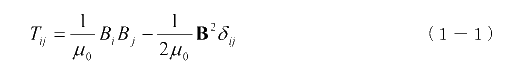
ここで、δijはクロネッカのデルタです。これを使うと磁性体に働く力は、

となります。ここでは誘電体の場合に約束したように、同じ項に現れる同じ添字については1から3までについての和をとるものとします。積分は力を計算する磁性体を完全に取り囲んだ体積領域Vについての体積積分です。面積分に直すと次のようになります。

ここに、Sは体積領域Vの境界面で、Vが磁性体を完全に取り囲んでいるため真空中にあります。またnはこの面の外向き
の単位法線ベクトルです。
磁性体全体ではなくこの磁性体の部分領域に働く力はどのように計算すればよいかを考えるために、誘電体の場合に議論したように、
マックスウェルの応力テンソルを修正して磁性体の部分領域も(1−3)式で計算できるようにすることを考えます。
まず(1−1)式において、真空の透磁率が含まれていることに着目します。真空中では磁束密度Bと磁場Hは、

の関係にありますから、これを使って次のように書き直します。

この式は真空中ではもちろん(1−1)式と同じになりますが、磁性体内部では異なった式になります。
はたしてこの式によって磁性体の部分領域にはたらく力が計算できるでしょうか。
誘電体に関する議論と同じように、今回は磁性体を磁気双極子の集まりとするモデルを考え、
(1−5)式が磁性体の部分領域の計算に妥当かどうか検討します。
2.磁気双極子の集合体に働く電磁力
ここでは磁性体を磁気双極子の集まりとしてモデル化します。もちろん実際の磁性体とは異なりますが、このようなモデル化により
物質中の電磁力を具体的に計算することができます。
磁気双極子としては環状電流が流れている円柱状の剛体を考えます。いま一つの磁気双極子に着目し、円柱の半径a高さh、円柱の側面に面密度Mの環状電流が
一様に分布しているものとします。この双極子の位置における平均磁束密度をBとし、この磁束密度の変化に対してa及びhは十分小さいとすればこの双極子の受ける力は次のように計算できます。一般性を失うことなく座標系の原点を今着目している円柱状絶縁体の中心にとり、z軸の向きを下面の中心から
上面に向かうようにします。このとき、表面電流密度Jが、
のように分布しているものとします。
円柱の側面の単位面積当たりに働く力fはローレンツ力より、
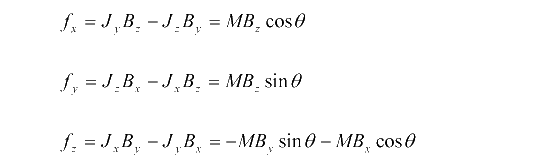
となります。a及びhは十分小さいので磁束密度分布は次のようにかけます。
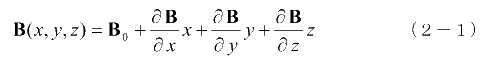
これより円柱側面の環状電流に働く力Fは、
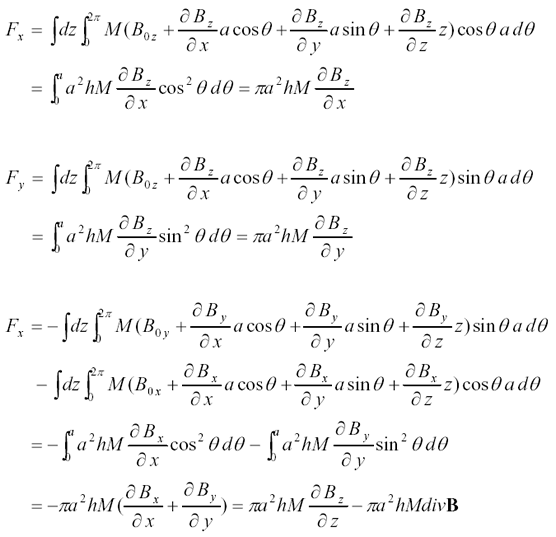
ですが、まとめて書くと次のようになります。
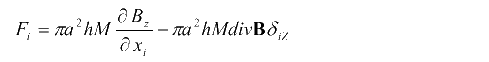
ここでπa2hMはこの円筒のz方向の磁気双極子モーメントmzですから、この式は次のように書けます。

この式は特別な座標系で表現されているが、一般の座標系で表現すれば、

となります。このような磁気双極子が数多く分布しており、各々の双極子モーメントmは大きさも方向もそろっていませんが、
単位体積中に含まれる双極子の数Nは一定とします。
ここで磁場の変化に対しては非常に小さいが、数多くの磁気双極子を含む領域ΔVを考え、次式で定義される単位体積あたりの
磁気双極子モーメントMを導入します。

Mは位置の関数となるので双極子の数が非常に多い場合は連続な場として考えることが出来ます。このときこれらの双極子の受ける
単位体積あたりの力fは次のようになります。

領域Vでこの式を積分すればこの領域に含まれる全ての双極子に働く力Fが計算できます。
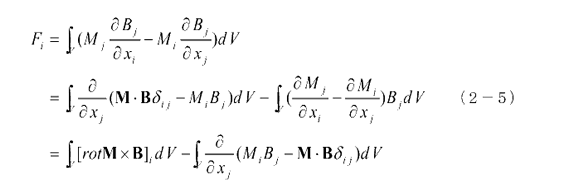
さらに右辺第二項を表面積分に変換すれば、
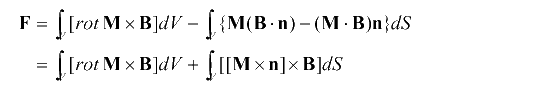
となります。ここに、Sは今考えている双極子集合体の部分領域Vの境界面であり、nはこの面に外向きに取った
単位法線ベクトルです。ここで、

は磁気双極子の環状電流による電流密度及び表面電流密度ですからこの式は次のようになります。
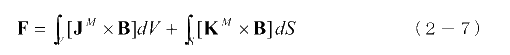
磁気双極子の作る平均的な電流密度と表面電流密度が、平均的な磁束密度からローレンツ力を受けるという非常に分かりやすい結果が得られました。
そこで磁気双極子集合体の部分領域がこのような力を受けるためには、電磁応力テンソルがどのように表現されないといけないかを調べます。
そのために、(2−5)式に戻るのですが、この磁気双極子の受ける平均の磁束密度がマックスウェルの方程式に従うことと(2−6)式より、

を満たさなければならないことに注意すれば(2−5)式は次のようになります。
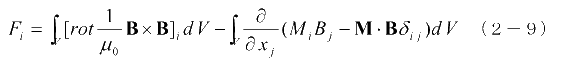
ここで右辺第2項の被積分関数を次のように変形します。
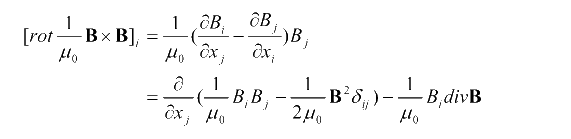
ここで、

なので(2−9)式は次のようになります。
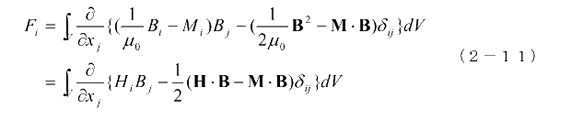
これより電磁応力テンソルは次のようになります。
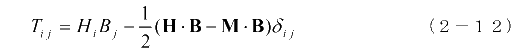
この式は予想された(1−5)式とは異なっていますが、今回の磁気双極子の集合体モデルによる議論では、磁性体の部分領域に働く力
はこの式で表されることを示唆しています。
