ここまでは非線形磁性体として等方性を仮定してきました。そのため磁化特性としては(3.2-3)式、
\begin{equation}
\boldsymbol{M}=f(|\boldsymbol{B}|)\frac{\boldsymbol{B}}{|\boldsymbol{B}|} \notag
\end{equation}
を採用したのですが、この式では磁束密度がゼロになると磁化もゼロとなり磁場 $\boldsymbol{H}$ もゼロとなります。
ところが永久磁石の場合磁束密度をゼロにするには保磁力 $H_c$ の磁場を逆向きにかける必要があります。
また下の図にあるように磁場がゼロのときも残留磁束密度 $B_r$ を持ちます。
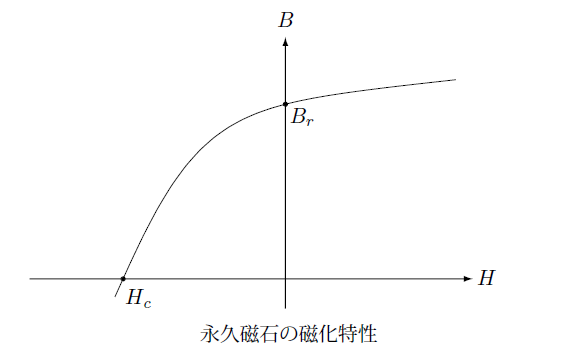
このような磁性体は(3.2-3)式で扱うことはできません。そこでこの式を次のように修正します。
\begin{equation}
\boldsymbol{M}=f(|\boldsymbol{B}|)\frac{\boldsymbol{B}}{|\boldsymbol{B}|}+\boldsymbol{M}_c \tag*{$(3.3-1)$}
\end{equation}
ここに $\boldsymbol{M}_c$ は磁石の磁化方向で大きさが保磁力の磁化ベクトルです。これより、
\begin{equation}
\boldsymbol{H}=\frac{1}{\mu_0}\boldsymbol{B}-f(|\boldsymbol{B}|)\frac{\boldsymbol{B}}{|\boldsymbol{B}|}-\boldsymbol{M}_c \tag*{$(3.3-2)$}
\end{equation}
となり、磁束密度がゼロの場合磁場は磁石の磁化方向とは逆に大きさが保磁力の値となります。
したがって永久磁石を扱うにはこの磁化ベクトル $\boldsymbol{M}_c$ を磁石の要素の要素ベクトルに足しこんでやればよいことになります。
(3.2-16)式の磁化に関する要素ベクトルを次のように修正します。
\begin{equation}
M_\alpha=\int_{V_n}\mathrm{rot}\boldsymbol{N}_\alpha\cdot(\boldsymbol{M}+\boldsymbol{M}_c)dV \tag*{$(3.3-3)$}
\end{equation}
磁石の透磁率 $\mu$ が線形の場合(3.3-1)式は次のようになります。
\begin{equation}
\boldsymbol{M}=(\frac{1}{\mu_0}-\frac{1}{\mu})\boldsymbol{B}+\boldsymbol{M}_c \notag
\end{equation}
また、(3.3-2)式は
\begin{equation}
\boldsymbol{H}=\frac{1}{\mu}\boldsymbol{B}-\boldsymbol{M}_c \notag
\end{equation}
となります。磁石の磁化が飽和磁化に近いときはこの透磁率は真空の透磁率 $\mu_0$ に近いので透磁率としてこの値を使ってもそれほど悪い近似ではありません。また上の図の磁化特性の第2象限が直線に近いときは、
\begin{equation}
\mu=\frac{B_r}{H_c} \tag*{$(3.3-4)$}
\end{equation}
として近似することもよくあります。
以上永久磁石の取り扱いをどうすればよいかを述べましたが、一般の非線形磁性体をどう扱えばよいかをこれから述べます。
まず考えられるのは、線形異方性磁性体の透磁率を拡張して透磁率を表す行列要素を磁束密度に依存させることです。
つまり、
\begin{equation}
\begin{bmatrix}
\mu_{11}(\boldsymbol{B}) & \mu_{12}(\boldsymbol{B}) & \mu_{13}(\boldsymbol{B}) \\
\mu_{21}(\boldsymbol{B}) & \mu_{22}(\boldsymbol{B}) & \mu_{23}(\boldsymbol{B}) \\
\mu_{31}(\boldsymbol{B}) & \mu_{32}(\boldsymbol{B}) & \mu_{33}(\boldsymbol{B}) \\
\end{bmatrix} \tag*{$(3.3-5)$}
\end{equation}
とします。これより、
\begin{equation}
B_i=\sum_j\mu_{ij}(\boldsymbol{B})H_j \tag*{$(3.3-6)$}
\end{equation}
とかけます。ここでは磁束密度が決まっていることを考えているので透磁率の逆行列 $\mu^{-1}$ を使って次のようにかきます。
\begin{equation}
H_i=\sum_k(\mu^{-1})_{ik}(\boldsymbol{B})B_k \tag*{$(3.3-7)$}
\end{equation}
両辺を磁束密度で微分すると次のようになります。
\begin{equation}
\frac{\partial H_i}{\partial B_j}=(\mu^{-1})_{ij}(\boldsymbol{B})+\sum_k\frac{\partial}{\partial B_j}(\mu^{-1})_{ik}B_k \tag*{$(3.3-8)$}
\end{equation}
先の線形異方性磁性体のところで透磁率を表す行列は対称でなければならないことを述べましたが、
\begin{equation}
\frac{\partial H_i}{\partial B_j}=\frac{\partial H_j}{\partial B_i} \tag*{$(3.3-9)$}
\end{equation}
も要請されます。
これをみたすためには関数 $\mu_{ij}(\boldsymbol{B})$ に対してかなり強い制限を加える必要がありこの形で非線形磁性体を扱うことは難しくなります。
それではなぜこのような要請があるのかをこれから説明します。そのために少し回り道になりますが磁性体の内部エネルギーの考察を行います。
まずベクトルの恒等式、
\begin{equation}
\mathrm{div}[\boldsymbol{E}\times\boldsymbol{H}]=\mathrm{rot}\boldsymbol{E}\cdot\boldsymbol{H}-\boldsymbol{E}\cdot\mathrm{rot}\boldsymbol{H} \tag*{$(3.3-10)$}
\end{equation}
から始めます。この式は数学的な恒等式なので物理的な意味を持っていませんが、ベクトル $\boldsymbol{E}$ を電場、$\boldsymbol{H}$ を磁場と考えれば、
物質中のマックスウェルの方程式から、
\begin{equation}
\begin{split}
&\mathrm{rot}\boldsymbol{E}=-\frac{\partial\boldsymbol{B}}{\partial t} \\
&\mathrm{rot}\boldsymbol{H}=\boldsymbol{J}+\frac{\partial\boldsymbol{D}}{\partial t}
\end{split} \notag
\end{equation}
なので上の式に代入すると次のようになります。
\begin{equation}
\mathrm{div}[\boldsymbol{E}\times\boldsymbol{H}]=-\frac{\partial\boldsymbol{B}}{\partial t}\cdot\boldsymbol{H}-\boldsymbol{E}\cdot\bigl(\boldsymbol{J}
+\frac{\partial\boldsymbol{D}}{\partial t}\bigr) \notag
\end{equation}
変形すると次のようにかけます。
\begin{equation}
\boldsymbol{E}\cdot\frac{\partial\boldsymbol{D}}{\partial t}+\boldsymbol{H}\cdot\frac{\partial\boldsymbol{B}}{\partial t}
=-\boldsymbol{E}\cdot\boldsymbol{J}-\mathrm{div}[\boldsymbol{E}\times\boldsymbol{H}] \tag*{$(3.3-11)$}
\end{equation}
この式の右辺は、右辺の第1項は電場が電流に単位時間あたりに与える仕事量であり第2項はポインティングベクトルによって失うエネルギーです。
これより左辺は単位体積当たりの電磁場が単位時間に行う仕事量と考えることが出来ます。
したがって、単位体積当たりの物質の内部エネルギーを $U$ とかけばこの単位時間当たりの変化はこの電磁場の時間変化によって次のように表すことが出来ます。
\begin{equation}
\frac{\partial U}{\partial t}=\boldsymbol{E}\cdot\frac{\partial\boldsymbol{D}}{\partial t}+\boldsymbol{H}\cdot\frac{\partial\boldsymbol{B}}{\partial t} \notag
\end{equation}
これより一般的に電束密度や磁束密度が変化したときの内部エネルギーの変化は次のようになります。
\begin{equation}
dU=\boldsymbol{E}\cdot d\boldsymbol{D}+\boldsymbol{H}\cdot d\boldsymbol{B} \tag*{$(3.3-12)$}
\end{equation}
ここでは電磁場の変化だけを考えましたが、実際にはこの変化の過程で外界との熱のやり取りがあります。単位時間にこの系が外界から受け取る熱量を $\delta Q$ とすれば、
\begin{equation}
dU=\delta Q+\boldsymbol{E}\cdot d\boldsymbol{D}+\boldsymbol{H}\cdot d\boldsymbol{B} \notag
\end{equation}
とかく必要があります。したがって熱のやり取りがない場合に限り(3.3-12)式を使うことが出来ます。
ここからはすこし熱力学的な話になります。
可逆な変化では、単位体積当たりのエントロピーを $S$、温度を $T$ とすれば、
\begin{equation}
\delta Q=TdS \tag*{$(3.3-13)$}
\end{equation}
となります。これより上の式は、
\begin{equation}
dU=TdS+\boldsymbol{E}\cdot d\boldsymbol{D}+\boldsymbol{H}\cdot d\boldsymbol{B} \tag*{$(3.3-14)$}
\end{equation}
となります。ここで重要なことはこの内部エネルギーは、$S$ や電磁場 $\boldsymbol{D}$、$\boldsymbol{B}$ の現在の値によって完全に決まってしまうことです。
すなわち、どのような過程を経てきたかは関係なく、
\begin{equation}
U=U(S,\boldsymbol{D},\boldsymbol{B}) \tag*{$(3.3-15)$}
\end{equation}
とかくことが出来ます。このような量のことを状態量とよんでおり、$S$、$\boldsymbol{D}$、$\boldsymbol{B}$ などを状態変数とよびます。
エントロピー一定の変化すなわち断熱変化ではエネルギーは重要な量ですが、等温変化を扱う場合次の式で定義される自由エネルギーを使う方が便利です。
\begin{equation}
F=U-ST \tag*{$(3.3-16)$}
\end{equation}
微分をとり(3.3-14)式を使うと次のようになります。
\begin{equation}
dF=dU-TdS-SdT=-SdT+\boldsymbol{E}\cdot d\boldsymbol{D}+\boldsymbol{H}\cdot d\boldsymbol{B} \tag*{$(3.3-17)$}
\end{equation}
この場合状態変数はエントロピー $S$ の代わりに温度 $T$ となりますから自由エネルギーは、
\begin{equation}
F=F(T,\boldsymbol{D},\boldsymbol{B}) \tag*{$(3.3-18)$}
\end{equation}
とかけ状態変数は、$T$、$\boldsymbol{D}$、$\boldsymbol{B}$ です。
自由エネルギーはエネルギーよりなじみが薄い量ですが、エントロピーではなく温度が変数となっているので扱いやすい量であることが分かっていただけたと思います。
さてここから非常に重要なことが導けます。まず、この式を微分すると次のようになります。
\begin{equation}
dF=\frac{\partial F}{\partial T}dT+\sum_i\frac{\partial F}{\partial D_i}dD_i+\sum_i\frac{\partial F}{\partial B_i}dB_i \tag*{$(3.3-19)$}
\end{equation}
これと(3.3-17)式を比較することによって次の式が得られます。
\begin{equation}
S=-\frac{\partial F}{\partial T} \hspace{10mm} E_i= \frac{\partial F}{\partial D_i} \hspace{10mm} H_i= \frac{\partial F}{\partial B_i} \tag*{$(3.3-20)$}
\end{equation}
ここでの自由エネルギーの微分は他の状態変数を一定にして行います。もう一度微分することによって次の関係が成立することが分かります。
\begin{equation}
\begin{split}
&\frac{\partial E_i}{\partial D_j}=\frac{\partial^2F}{\partial D_i\partial D_j}=\frac{\partial E_j}{\partial D_i} \\
&\frac{\partial H_i}{\partial B_j}=\frac{\partial^2F}{\partial B_i\partial B_j}=\frac{\partial H_j}{\partial B_i}
\end{split} \tag*{$(3.3-21)$}
\end{equation}
この関係から線形誘電体や線形磁性体は異方性を持っていても対称行列で表されることが導かれます。また、この関係は前に言及した(3.3-9)式と同じです。
ここからは磁性体に話を戻します。磁性体の単位体積当たりの自由エネルギーは温度と磁束密度の関数です。
\begin{equation}
F=F(T,\boldsymbol{B}) \tag*{$(3.3-22)$}
\end{equation}
磁性体を一様に磁化させる場合磁化の方向と大きさによってエネルギーは決まりますが、磁化の向きは逆向きに着磁させても同じです。
これは自由エネルギーの場合も同じなので磁束密度の各成分の二乗の関数となるはずです。したがってこの式は、
\begin{equation}
F=F(T,B_x^2,B_y^2,B_z^2) \tag*{$(3.3-23)$}
\end{equation}
とかけます。この式をこの磁束密度の成分で展開すると次のようになります。
\begin{equation}
F(T,B_x^2,B_y^2,B_z^2)=C_{000}(T)+\sum_{n=1}^\infty\sum_{k+l+m=n}C_{klm}(T)(B_x^2)^k(B_y^2)^l(B_z^2)^m \tag*{$(3.3-24)$}
\end{equation}
ここに $C_{ijk}(T)$ は展開係数で温度の関数となっています。また $C_{000}(T)$ は磁場に依存しない自由エネルギーです。
(3.3-21)式より、
\begin{equation}
H_i=\frac{\partial F}{\partial B_i} \notag
\end{equation}
なのでこの式にこの展開した式を代入すると次のようになります。
\begin{equation}
\begin{split}
&H_x=\sum_{n=1}^\infty\sum_{k+l+m=n}2kC_{klm}(T)B_x^{2k-1}(B_y^2)^l(B_z^2)^m \\
&H_y=\sum_{n=1}^\infty\sum_{k+l+m=n}2lC_{klm}(T)(B_x^2)^kB_y^{2l-1}(B_z^2)^m \\
&H_z=\sum_{n=1}^\infty\sum_{k+l+m=n}2mC_{klm}(T)(B_x^2)^k(B_y^2)^lB_z^{2m-1}
\end{split} \tag*{$(3.3-25)$}
\end{equation}
展開次数を有限の値で近似し測定値と比較することによってこの展開係数を決めることが出来ます。それにより自由エネルギーの関数形が決まりますのでこの方法で非線形の異方性磁性体を扱うことは可能です。
ただしこの方法ですとあらゆる方向についての磁束密度と磁場の関係を磁束密度の大きさごとに分かっていなければならずデータの入手が困難です。
これに関してはもう少し実用的観点からこのようなデータの必要がない方法について検討します。
技術情報 Techinicalinfo
- ホーム
- 技術情報
- 【技術情報】有限要素法入門
- 3.3 異方性非線形磁性体
【技術情報】有限要素法入門
