1.ミクロな電磁場
私たちが通常電磁場と呼んでいるものはマクロな電磁場です。物質はミクロに見ると原子からできています。原子はプラスの電荷をもった原子核とマイナスの電荷を持った電子からできており原子核の大きさは原子の10万分の1程度です。ですから原子の内部はほとんど真空領域と考えてよくその原子からできている物質も内部は大部分が真空と考えることができます。さらに原子核は陽子や中性子からできており、現代物理ではこれらの陽子や中性子もクォークからできていると考えられています。そしてこれらの基本粒子と考えられているクォークや電子などは大きさがあるかどうかも分かっていません。したがって物質はほとんど大きさの無視できる莫大な数のクォークや電子などの電磁場の発生源とそのほとんどの領域を占める真空領域からできていると考えることができます。
そこでこれら電磁場の発生源の電荷密度をρとしてミクロな電磁場について考えます。クォークや電子がどのような電荷密度を持っているか分かりませんが非常に小さな領域だけに値がありそれ以外はゼロであると考えられますし、もし大きさがなければディラックのデルタ関数のような分布となります。
ここでミクロな電場eと電束密度d、およびミクロな磁場hと磁束密度bを導入します。これらの間には真空の誘電率εと真空の透磁率μをつかって次のように関係付けられています。

この関係は真空領域だけでなく電磁場の発生源である電荷密度ρが存在するところでも成り立っていると考えます。このときこれらミクロな電磁場に対して次のマックスウェルの方程式が成立します。

ここでvは電荷密度の速度です。電磁場の発生源である電荷密度は非常に狭い範囲に局在しているためその付近で電荷密度が大きく変化し、それに伴なってミクロな電磁場も激しく変化すると考えられます。はじめに言いましたが通常私たちが問題にしている電磁場はこのようなミクロな電磁場ではなく、これらを平均化したものです。そこで今回はこのようなミクロな電磁場とマクロな電磁場がどのような関係にあるかについて調べます。
2.ミクロな量の平均操作
ここでは空間に分布しているミクロな量の平均操作について考えます。そのためにマクロで見ると非常に小さな微小領域ΔⅤを考えます。この領域はマクロに見ると大きさが無視できる程、つまりそこに含まれる物質の状態が均質とみなせる程小さいのですが、ミクロで見ると平均操作が充分意味を持つために必要な多くの電磁場の発生源を含んでいるものとします。ミクロな量をf(x,y,z,t)としたときこの領域について次のように平均操作を定義します。
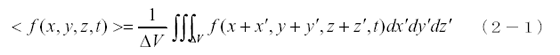
この積分は座標(x+x’,y+y’,z+z’,t)がΔⅤに含まれる領域で行います。これより、
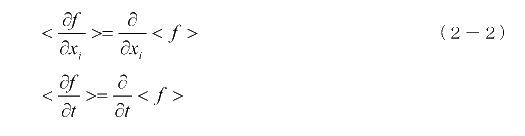
が成立することが分かります。これを使ってマックスウェルの方程式(1-2)式の平均をとると次のようになります。
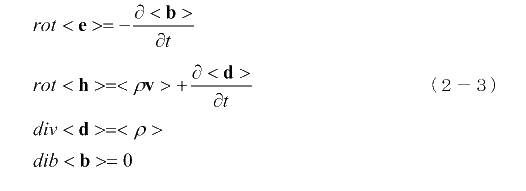
また(1-1)式の平均をとると次のようになります。

3.誘電体
物質を構成している原子や分子は電気的にプラスの電荷とマイナスの電荷を同じ量だけ含んでいますので電気的に中性ですが、電荷の分布はプラスとマイナスで異なりますので電気的なモーメントを持っています。通常私たちが接する物質は莫大な数のこれらモーメントの平均によりキャンセルする状態にありますので、電気的に中性で電場の発生源になりません。しかしこの物質の外から電場をかけると物質中のモーメントが変化し電気を帯びるようになります。このような物質を誘電体と呼んでいます。
誘電体が電気を帯びるこのような現象を定量的にもう少し詳しく調べてみます。最初誘電体内部のミクロな電荷分布をρ0とします。もちろんρ0は空間的にも時間的にも変動していますがこれを平均したマクロな電荷密度は、

です。ここで外から電場がかけられたとします。このときミクロな電荷密度が変化を受け位置がgだけ変位したとします。これは電子の軌道が外部電場の影響で少し移動したり、分子の持つモーメントの方向が変化したりすることによるものと考えられますが、このような物質の具体的な構造を知らなくても一般論として議論することができます。この位置の変化によって物質中では、ρgの電荷の移動が生じます。これを平均したものを、

と定義しますとこの量はマクロなベクトル場として扱うことができます。このような電荷の移動によって物質中のマクロな電荷密度はもはや(3-1)式を満たさなくなります。それは物質中の微小領域ΔⅤを考えた場合、この表面ΔSから、

の電荷が流出します。ここでnは積分面の領域から外向きにとった単位法線ベクトルです。これよりこの領域における電荷の変化は次のように表すことができます。

この積分は微小領域ですがマクロな領域における積分なのでこの式の両辺を平均することができます。この式の左辺にある変化を表すΔは積分の中に入れることができ、もともとゼロだった電荷密度の増分を、

と書き、(3-2)式を使うと次のようになります。
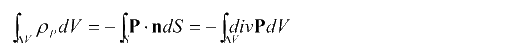
最後の式はガウスの発散定理によって表面積分を体積積分に変えています。ここで積分した微小領域は任意に取ることができますので次のように書くことができます。

このように電気的に中性な物質も外から電場をかけることによって電気的な性質が変化します。これを分極と呼び、この結果出てきた電荷密度ρ0を分極電荷、また(3-2)式で定義された電荷移動の平均を分極ベクトルと呼びます。以上のことから誘電体中では平均化されたマックスウェルの方程式(2-3)式の第3式は次のようになります。

4.磁性体
磁気を持たない物質でも外部から磁場をかけると磁気を帯びることがあります。これはマクロにみると磁気を帯びていないように見える物質も、電子の軌道運動によるミクロな電流や、電子のスピンなどによる磁場などが平均すると相殺されて、

を満たしていますが、外部の磁場によって物質中のミクロな電流の分布やスピンの向きなどが変化し(4-1)式をみたさなくなったからだと考えることができます。
これは誘電体の電荷が普段は相殺されて(3-1)式をみたしているのに外部から電場をかけると分極電荷が現れるのと似た現象です。このように、外部から磁場をかけることによって磁気を帯びる物質を磁性体と呼んでいます。最初磁性体内部のミクロな電流分布をj0とします。j0は空間的にも時間的にも変動していますがこれを平均したマクロな電流密度は、

です。ここで外から磁場がかけられたとします。このときミクロな電流密度が変化を受けjmとなったとします。この電流は平均してもゼロとならず平均値を、

と定義しますとこの量はマクロなベクトル場として扱うことができます。この電流は磁性体内部で電荷を作ることがないので次の関係を満たす必要があります。

ベクトル解析よりこのような関係を持つベクトル場は次のようにかけます。

ここにMはマクロなベクトル場で(4-5)式をみたすように定義されているため任意性があります。そこで磁性体以外ではゼロとなるようにします。
このように磁気を帯びていない物質も外から磁場をかけることによって磁気的な性質が変化します。これを磁化とよび、この結果出てきた電流密度
jmを磁化電流、また(4-5)式で定義された磁性体中のベクトル場Mを磁化ベクトルと呼びます。
以上のことから磁性体中では平均化されたマックスウェルの方程式(2-3)式の第2式は次のようになります。

5.マクロな電磁場
誘電体内部では(3-1)式が成り立ち電荷密度の平均がゼロであるとしたのですが一般的には分極電荷以外の自由電荷が存在するので
この電荷の平均を真電荷密度、

としますとこの電荷密度はマクロな量となります。同じ文字ですが右辺の平均をとる前の電荷密度は全てのミクロな電荷密度を含んでいますが分極に寄与する電荷は通常相殺されて平均はゼロとなっています。真電荷を考えると(3-6)式は次のようになります。

分極の定義である(3-2)式より分極の時間的変化はミクロな電流を作ります。この式の両辺の時間微分をとり時間微分と平均操作の順を入れ替えてよいことに注意すれば次の関係が得られます。

これより、
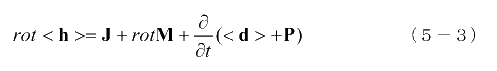
となります。(5-2)式と(5-3)式は変形すると次のようにかけます。
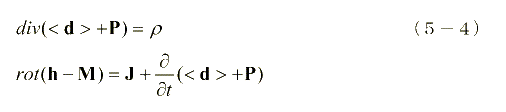
そこでマクロな電磁場を次のように定義します。

これより平均化されたマクロなマックスウェルの方程式は次のようになります。

(2-4)式と(5-5)式より次のマクロな電磁場の関係が得られます。

以上の議論から、次のような結論が得られるように思われます。
「マクロな電磁場のうちミクロな電磁場を平均して直接得られる場は、電場Eと磁束密度Bであり、電束密度Dや磁場Hは誘電体や磁性体を取り扱うのに便利なために導入された便宜的な場である。」
これより、電場と磁場の対応関係においてEに対応するのがB、Dに対応するのがH、というE-B対応という見方が自然であるという考えが現在では主流になっているようです。一方マクロな電磁場についてのマックスウェルの方程式(5-6)式を見ると、Eに対してH、Dに対してB、が同じ役割をしているように見えます。
そこでこれらの間に対応関係があるとする見方をE-H対応とよんでいます。
E-B対応とE-H対応に関しては議論しなければならないことが色々とありますので、また改めて考察したいと思っています。
いずれにしましても、複雑な物質中の電磁場のふるまいが平均すると(5-6)式のような簡単な方程式にまとめられるのは驚異的なことです。ただし実際にこの方程式を解くためには物質ごとに(5-7)式で表される構成方程式を考える必要がありますので見かけほどは簡単ではありません。
