概 要
本解析事例では、円筒型コンデンサーの静電容量の計算値と理論解との比較をご紹介致します。
以下の3条件について、解析致しました。本事例は静電場解析ですので、VOLTだけでなく、VOLTjωでも解析可能です。
1.円筒型コンデンサー(空気)
2.円筒型コンデンサー(誘電体-径方向2層)
3.円筒型コンデンサー(誘電体-周方向2層)
円筒型コンデンサー(空気) 解析結果
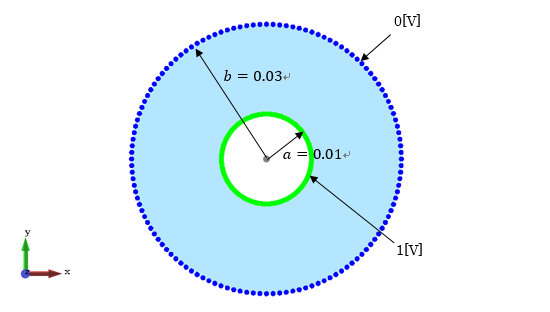
図1−1.概要図
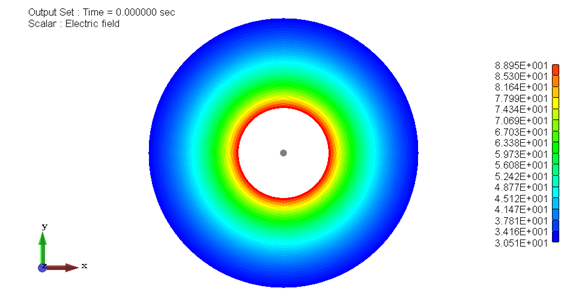
図1−2.電界分布[V/m]
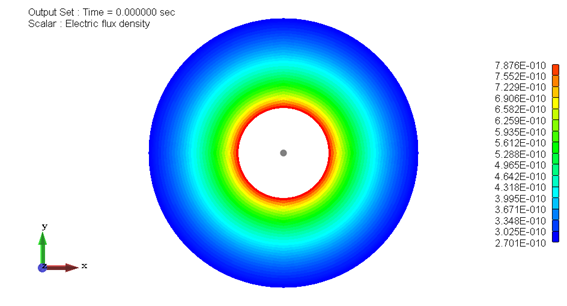
図1−3.電束密度分布[C/m2]
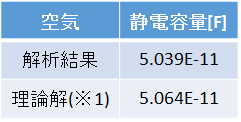
表1−1.静電容量(単位長さ当たり)
使用ソフトウェア:PHOTO-VOLT もしくは VOLTjω
円筒型コンデンサー(誘電体-径方向2層) 解析結果
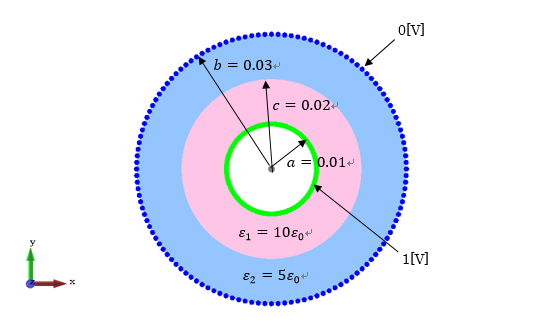
図2−1.概要図
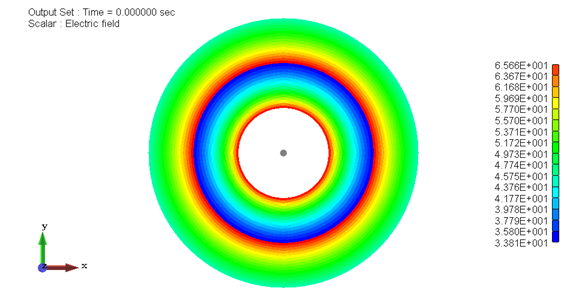
図2−2.電界分布[V/m]
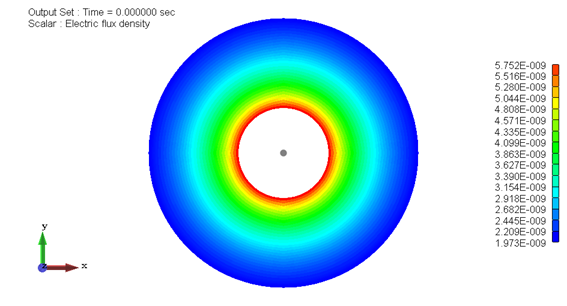
図2−3.電束密度分布[C/m2]
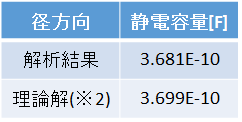
表2−1.静電容量(単位長さ当たり)
円筒型コンデンサー(誘電体-周方向2層) 解析結果
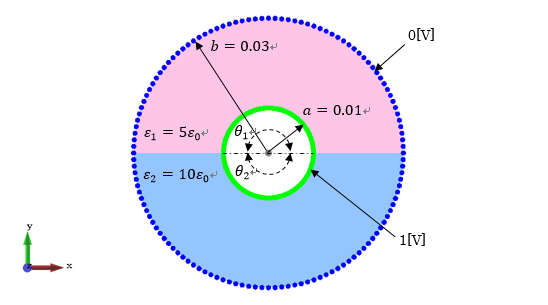
図3−1.概要図
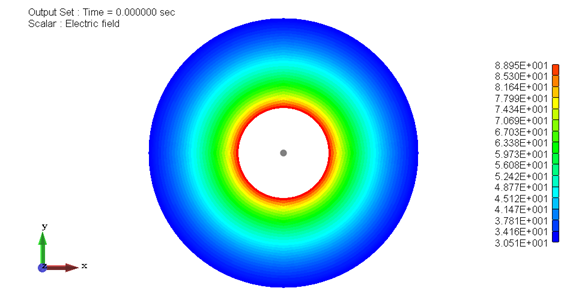
図3−2.電界分布[V/m]
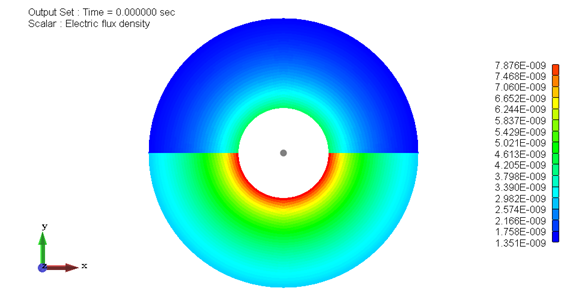
図3−3.電束密度分布[C/m2]
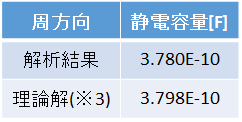
表3−1.静電容量(単位長さ当たり)
※1 円筒型コンデンサー(空気) 理論解

図1−1.概要図(再掲)
ガウスの法則
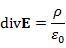
の体積積分をとり、ガウスの定理(体積積分から面積分へ)を適用します。
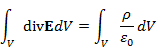
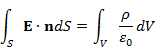
単位長さ当たりの電荷をλとすると、半径Rの位置における電場は
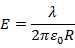
となり、
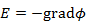
より、ポテンシャルは
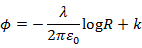
となります。電位差は
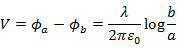
と表すことができます。単位長さ当たりの静電容量Cは
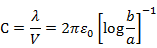
となります。
※2 円筒型コンデンサー(誘電体-径方向2層) 理論解

図2−1.概要図(再掲)
今回は誘電体が充填されていますので、真空の誘電率から誘電体の誘電率へ変更します。電場及びポテンシャルは、
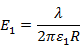
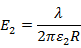
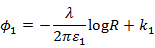
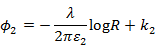
電位差は
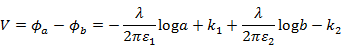
ここで、R=cの境界ではポテンシャルが同じ値になることから、
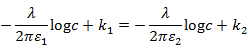
変形すると、
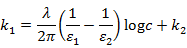
となり、電位差は
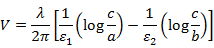
となります。よって、単位長さ当たりの静電容量は、
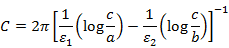
となります。ちなみに、c=b、ε1 = ε0とすると、空気の場合の静電容量と一致します。
※3 円筒型コンデンサー(誘電体-周方向2層)理論解

図3−1.概要図(再掲)
ガウスの法則
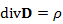
ここで、電束密度Dは
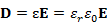
です。ここで、ε、εrはそれぞれ、誘電率、比誘電率です。体積積分をとり、ガウスの定理(体積積分から面積分へ)を適用します。積分面が分割されていることを考慮しますと、
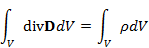
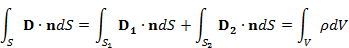
となります。角度θの円弧の長さはθRであることから、
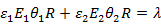
となります。一方、誘電体1と誘電体2の境界では、電場の連続性により、
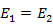
となります。この電場を改めてEとしますと、
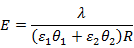
となります。よって、ポテンシャルは
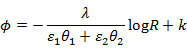
となりますしたがって、電位差は
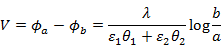
と表すことができます。単位長さ当たりの静電容量Cは
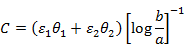
となります。
