八木・宇田アンテナは、複数の短い素子からなる導波器と長い素子の反射器、そしてその間に位置する給電器から構成される指向性を持ったアンテナです。給電器から放射される電磁波を有限要素法により解析し、その結果をもとに遠方の平面波を推定します。給電器から電場がZ軸方向に偏波した電磁波を放射させ、アンテナ全体を包む空気領域内の電磁波の様子を有限要素法により解析します。次にその結果をもとにして遠方での電磁波を２種類の方法で推定し、その結果を比較します。形状はフルモデルとしました。
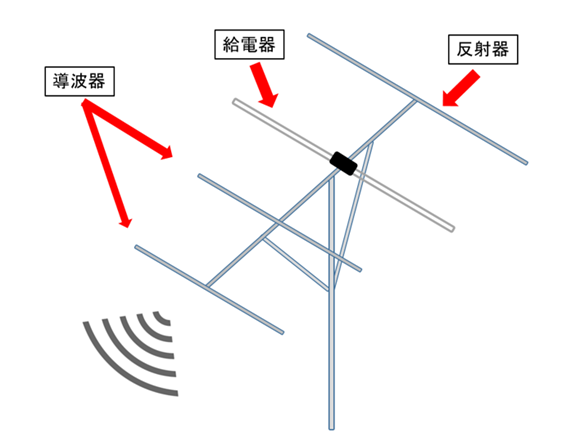
図１−１．概要図(4素子)
使用ソフトウェア：PHOTO-WAVEjω
解析条件
■アンテナの解析モデルについて（４素子アンテナの場合）
図２−１．メッシュ図(全体 ２分の1カット図)
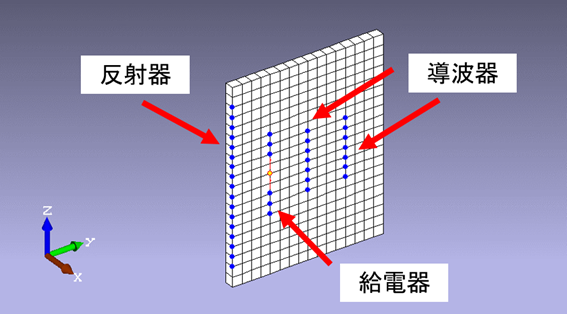
図２−２．メッシュ図(アンテナ部)
■解析モデルについて
まず、給電器から放射される電磁波を解析します。空気層（図２−１．）の中にアンテナ（図２−２．）を設置します。
アンテナ素子は完全導体として扱います。各々の素子のサイズは、波長を「λ」として
反射器・・・λ/2以上 給電器・・・ λ/2 導波器・・・ λ/2以下
とします。また、各素子の間隔は λ/4 とします。
空気層の外周には「インピーダンス境界」を設定し、「無反射境界条件」とします。
解析モデルの図は「４素子」の場合ですが、「５素子」のモデルも解析対象とし、結果を比較します。
■放射する電磁波について
大きさ ・・・ Z軸方向 1 [V/m]
周波数 ・・・ 1 G [Hz] 波長 λ = 3.0×10-1 [m]
■電磁波を推定する遠方場の観測点 半径 1.0 [m] の円
図２−３．は、給電器からの電磁波を解析した結果を使い、２種類の方法で推定する際に使うモデルです。
図２−３．メッシュ図(２分の1カット図)
遠方場の推定方法については2種類の方法があります。
■その１：外場計算による方法
「PHOTO-Series」に従来からある方法で、「図２−１．のモデル」の有限要素法による解析結果を「外場ファイル」として読み込み、「図２−３．のモデル」を解析対象として「外場計算」する方法です。
■その２：多重極展開による方法
「PHOTO-Series Version 9.2」 で機能追加した方法で、平面波を原点を中心とした「多重極」に展開した関数により遠方場を計算する方法です。「図２−１．のモデル」の有限要素法による解析結果を使い、原点に置いた多重極による平面波の散乱波の関数の係数を決定します。そして、この関数を使い「図２−３．のモデル」を解析対象にして計算します。
■解析結果１ アンテナ近傍
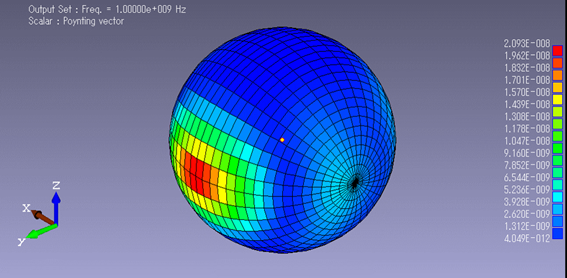
給電器から発信される電磁波の、空気層における「ポインティングベクトル」コンター図
図３−１−１．４素子アンテナ ポインティングベクトルコンター図
図３−１−２．５素子アンテナ ポインティングベクトルコンター図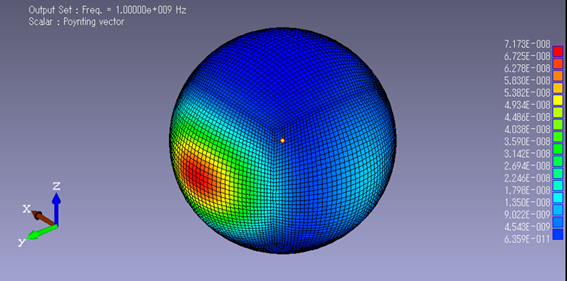
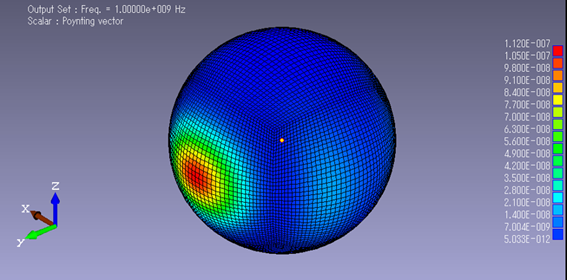
■解析結果２：４素子アンテナでの遠方場
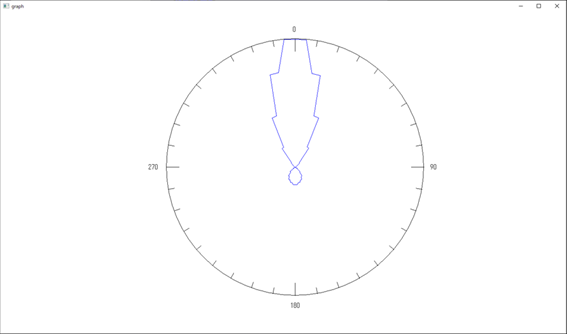
半径:1[m] における電磁波《その１：外場計算の場合》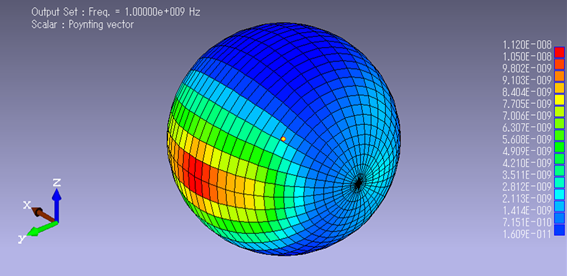
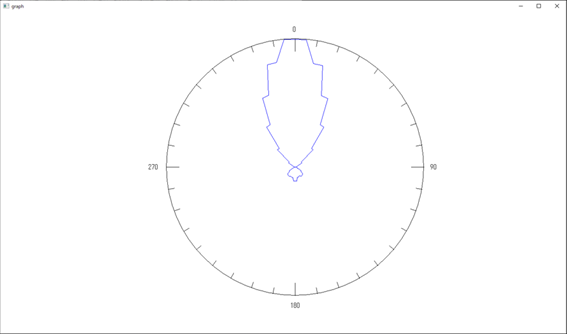
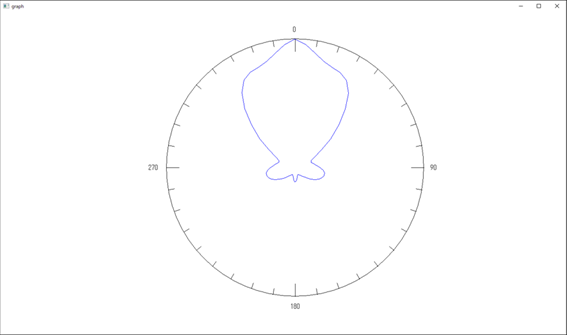
図３−２−１．ポインティングベクトルコンター図
図３−２−２．Y-Z面における中心から周方向へのポインティングベクトルの大きさ（進行方向：上方向）
図３−２−３．X-Y面における中心から周方向へのポインティングベクトルの大きさ（進行方向：上方向）
半径:1[m] における電磁波《その２：多重極展開の場合》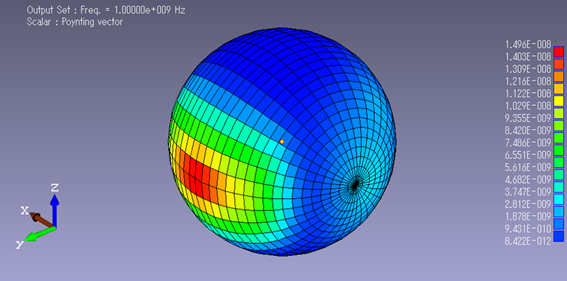
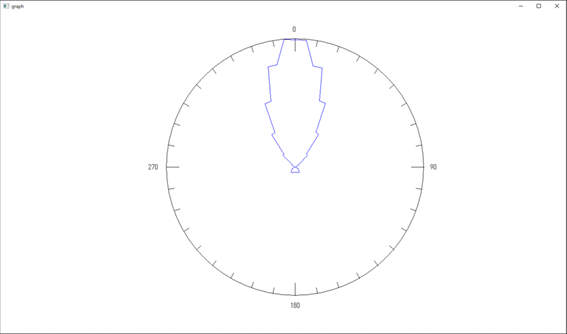
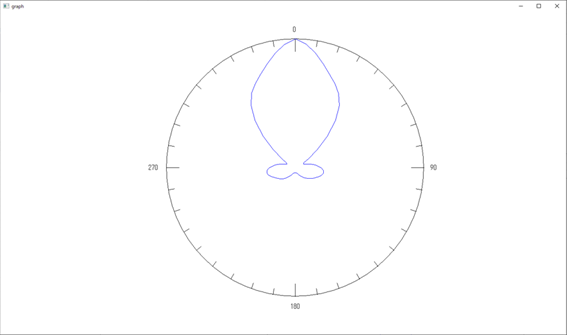
図３−２−４．ポインティングベクトルコンター図
図３−２−５．Y-Z面における中心から周方向へのポインティングベクトルの大きさ（進行方向：上方向）
図３−２−６．X-Y面における中心から周方向へのポインティングベクトルの大きさ（進行方向：上方向）
■解析結果３：５素子アンテナでの遠方場
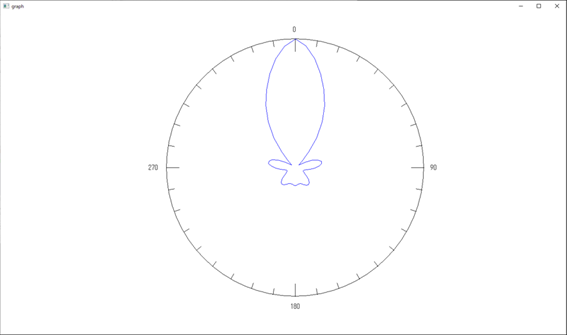
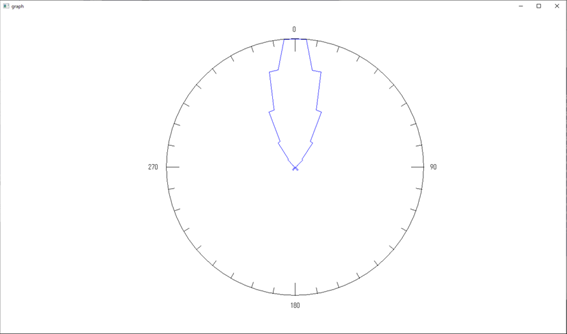
半径:1[m] における電磁波《その１：外場計算の場合》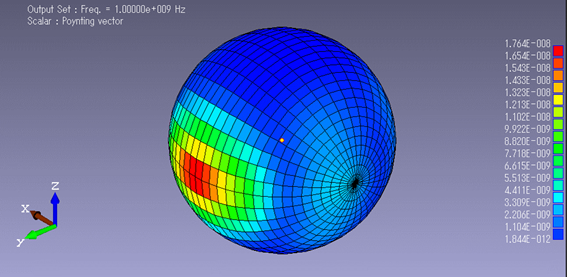
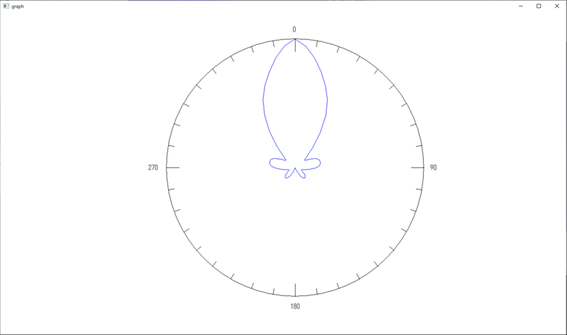
図３−３−１．ポインティングベクトルコンター図
図３−３−２．Y-Z面における中心から周方向へのポインティングベクトルの大きさ（進行方向：上方向）
図３−３−３．X-Y面における中心から周方向へのポインティングベクトルの大きさ（進行方向：上方向）
半径:1[m] における電磁波《その２：多重極展開の場合》
図３−３−４．ポインティングベクトルコンター図
図３−３−５．Y-Z面における中心から周方向へのポインティングベクトルの大きさ（進行方向：上方向）
図３−３−６．X-Y面における中心から周方向へのポインティングベクトルの大きさ（進行方向：上方向）